Pid control tutorial

원글 : https://smithcsrobot.weebly.com/uploads/6/0/9/5/60954939/pid_control_document.pdf

개요

PID란 원래 프로그래밍에서 사용되는 것으로, 적절히 튜닝 된다면 매우 효과적이고 정확한 결과를 가져올 수 있는 method이다.
PID는 Proportional Integral Derivative의 약자로, 세 개의 독립적인 인자를 합쳐 놓은 것이다. 단, 세 개를 전부 사용하지는 않을 수도 있다.
예를 들어, P Control를 할수도 있는거고, PI control만 할수도 있는거고 PD control을 할 수도 있는 것이다.
이 글에서는 Pseudocode로 PID control에대한 예시를 몇 개 기술해놓았다.
실제 사용가능한 코드는 아니지만, 이해에는 충분할 것이다

P - Proportional (비례)

어떤 로봇이 최고 속도로 1000만큼을 달리려 한다면, 이때 로봇은 로봇의 속도와 관성에 의해 1000보다 조금 더 나아가게 된다(Overshoot).
이러한 요소는 프로그램의 정확도을 저해시키는 요인이 되고, 프로그래머에게 골칫덩어리같은 존재가 된다.

그래프를 통해 보면,
이상적인 세계에서는 로봇에게 정지를 명령하면 로봇은 그 자리에서 바로 멈출 것이다.
(x축의 초록 막대 = 기존에 이동하려던 거리)

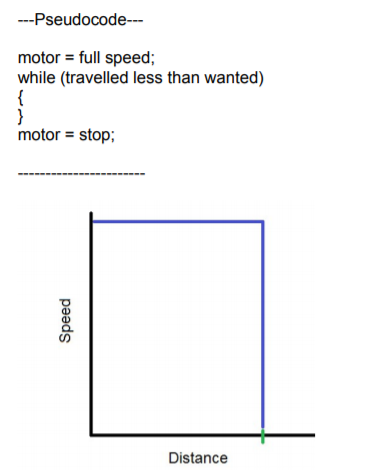
하지만 우리는 이상적이지 않은 세계에서 살고있고, 로봇에게 갑자기 정지를 명령하게 되면 overshooting 문제가 발생하게 된다.

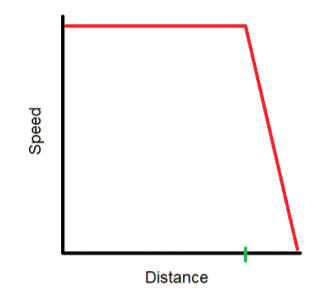
만약 이 overshooting이 항상 일정하게 일어난다면야 문제가 안되겠지만, overshooting에는 많은 변수가 존재한다.
그 중 몇 개를 소개하자면 아래와 같다.

• 배터리의 전압 : 배터리 전압이 낮다면 모터는 빠르게 회전하지 못하고 로봇은 작은 관성을 갖게되어 overshooting 또한 작게 일어날 것이다.
• 로봇이 진행중에 어떤 물체에 충돌한다면 overshooting은 감소할 것이다.
• 무언가가 로봇을 진행방향으로 밀어버린다면 overshoting은 더 커질 것이다.

따라서 우리는 P Controller를 이용해 목적지에 로봇이 가까워짐에 따라 속도를 감소시켜 Overshooting을 감소시켜야 한다. 그리고 이러한 작용, 즉 output speed를 어떤 변화해야하는 값(목적지까지 남은 거리)에 비례하여(propotional) 제어하는 작용을 수행하기 때문에 이것을 proportional controller라고 말한다. 이때 변화해야하는 값을 error라고 말한다.

이제 P Controller가 실제로 어떻게 작용하는지 알아보자.

Error라는 변수에 대해 이야기해보면, 이것은 sensor들로부터 얻어낸 바뀌어야하는 값이다.
예를 들어 error는 추가로 더 가야할 거리가 될 수도 있고, 추가로 더 들어올려야 할 높이가 될 수도 있고, 추가로 더 가열시켜야 할 온도가 될 수도 있다.

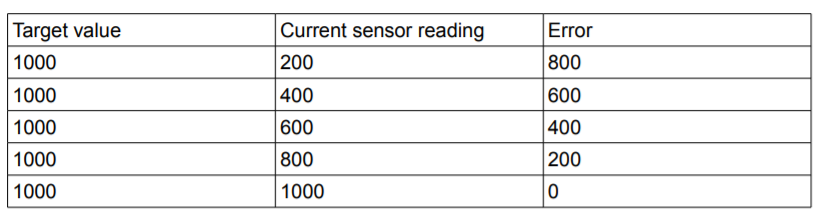
Error를 계산하려면, 원하는 target value에서 센서들이 읽어들이는 값을 빼면 된다.

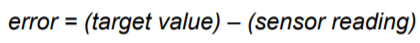
따라서 처음 로봇에 명령한 목표 거리 값과 현재 로봇이 지나온 거리를 안다면, 로봇이 목표에 가까워짐에 따라 error는 계속해서 감소할 것이다.

I나 D controller까지 쓰기는 귀찮다면 단순히 P 컨트롤러만 이용해도 로봇의 속도를 조절할 수는 있다.

이때 error값이 우리가 생각한 것과 다르게 나올 수도 있다.
Error 값이 너무 커서 목표지점에 대해 과도한 overshoot가 발생하게 되면, 로봇은 다시 그 overshoot를 수정하려 할 것이고, 그때 error는 음수가 될 것이다.
위 과정을 디버거 등으로 관찰한다면, error가 overshooting과 over-correcting을 반복하며 진동하는 것을 볼 수 있을 것이다.

반대로 error가 너무 작은 경우도 있겠지만, 이 경우는 별 문제가 되진 않을 것이다.

위와 같은 문제 때문에, 비례적인 요소를 유지하며 error를 변경함과 동시에 또 다른 상수를 error에 곱하거나 나눠주어야 한다.
일반적으로 이때 사용하는 상수를 Kp라고 부른다.

위 pseudocode가 P controller를 나타낸 것이다.
여기서 Kp는 0.5로 설정하였는데, 이는 임의로 결정한 것으로 그 값은 경우에 따라 달라진다. 정확한 Kp 값은 후에 찾아보는 시간을 가질 것이다.

이제 마지막으로, value들이 변화함에 따라 error 또한 다시 계산되어야 하므로 전체 코드를 루프에 집어넣는다.

I - Integral (적분)

Proportional part에 의해 error는 결국 매우 작아지게 될 것인데, 이렇게 error가 너무 작아지게 되면 그를 충분히 반영하기가 어려워 진다.
따라서 이러한 이유로 Integral을 도입하게 된다. 이때 Integral이란 지난 error들을 계속해서 더해 나가는 것을 의미한다.

Integral은 overshooting을 일으키지 않으면서 error를 감소시킬 수 있는 정도의 속도로 로봇을 움직이는 것이 목표이기에, Integral은 로봇을 서서히 가속시켜 속도를 정한다.

Integral은 위와 같이 계산 되는데, 등호 오른쪽 integral은 과거의 integral값이고 dT는 delta time을 말한다. delta time은 후에 다시 설명할 것이다.

Integral값이 증가하는 모습은 아래 표와 같다. 이때 error는 2로 설정하였다.
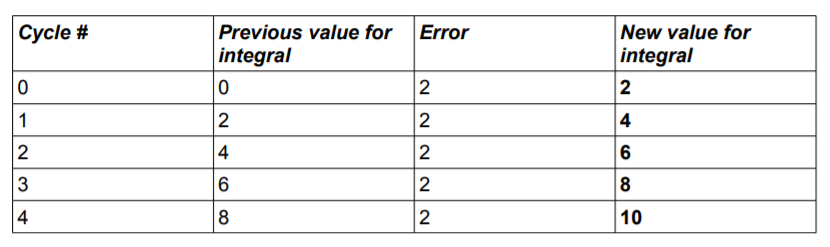볼드체로 표기한 숫자가 증가하는 것을 볼 수 있을 것이다.


그래서 이것을 어떻게 기존 코드에 더할까? 그냥 말그대로 더해버리면 된다.

Pseudocode를 다시 살펴보면,

Proportional code를 다루었을때와 마찬가지로, integral에 상수항을 하나 추가해 주어야 한다. Kp 때처럼 Ki에도 임의의 숫자 0.2를 넣어 주자

이제 delta time에 관해 설명하자면,
delta time은 루프가 한 사이클을 도는데 걸리는 시간이 일정하지 않을 때 필요한 요소이다.
따라서 한 사이클을 도는데 걸리는 시간이 일정하다면 이는 Ki에 병합될 수 있다. 만약 그렇지 않다면 코드 안에 각 사이클을 도는데 걸리는 시간을 측정하여 delta time으로서 사용하도록 하면 된다.
이 글에서는 사이클에 걸리는 시간이 항상 일정하다 가정하여 delta time을 Ki에 병합시킬 것이다.

Integral을 적용할때 발생하는 문제..

첫번째 문제

최종적으로 error가 0이 되어도 integral은 아직 error를 변화시킬 수 있는 속도를 출력시킬 값을 그대로 가지고 있을 것이다.
Error가 0이 되는 지점을 지나 error가 음수가 되어 기존의 integral 값에서 error를 빼는 형태가 되어야 비로소 integral은 스스로 0이 될 수 있을 것이다.
이러한 문제를 해결하기 위해서, error가 0이 되면 integral을 reset해주는 과정이 필요하다.

두번째 문제

흔히 Integral wind-up 이라고 일컫는 문제이다.
이는 이동해야 할 error(남은 거리)의 크기가 큰 상태에서 integral이 build up 되면 발생하는데, 이렇게 되면 integral의 값이 너무 커져서 이용하기 어렵게 된다.

위 문제에는 세 가지 해결책이 있다.

첫번째 해결책

Integral 값의 상한선과 하한선을 정하기

두번째 해결책

Integral 값의 범위를 정해 만약 그 범위를 넘어가게 되면 integral을 disable하기

• 이때 integral에 음수값이 들어올 수도 있기에 절댓값을 이용하거나 음수에도 범위를 정해주어야 한다.

세번째 해결책

Integral이 build up 되는 시간을 제어하기

이 글에서는 2번(범위) 해결책을 이용할 것이다.
이를 적용한 코드는 아래와 같다.

D - Derivative (미분)

이제 PID의 마지막 조각인 Derivative이다.
Derivative는 미래의 error값을 예측하여 그에 따라 속도를 조절하는 역할을 한다.
예를 들어, 로봇이 overshoot할 것으로 예측되면 Derivative는 로봇이 속도를 미리 줄이도록 작용한다.
이때 미래에 일어날 error를 예측하기 위해서는 과거의 error를 구해 현재의 error와 과거의 error의 차를 구해야 한다.

위와 같은 식을 통해, 현재의 error와 과거의 error 사이의 변화량을 구해 현재의 error에 더함으로써 미래의 error값을 예측할 수 있다. 이때 Integral과 마찬가지로 derivative 또한 dT에 영향을 받는데, 루프의 수행 시간이 일정하다고 가정하면 dT는 Kd값에 병합시켜 생각할 수 있다.

아래의 표는 derivative를 이용하여 미래의 error를 예측한 것이다.

이 글의 코드에서 derivative는 위의 등식을 이용해 계산되어 속도 값에 더해지도록 할 것이다. 이때 scaling을 위해 Kd를 곱해준다.

또한 과거의 error 값을 보관할 정수를 하나 만들어 derivative를 계산하고 나면 자동으로 업데이트하도록 해야한다. 이때 업데이트는 현재의 error의 값과 같게 설정되도록 하면 될 것이다.

완성된 Pid Controller Pseudocode는 아래와 같다.

위 코드에서 파란색은 proportional 요소를 의미하고 빨간색은 Integral 요소, 초록색은 derivative 요소를 의미한다.

상수 값 튜닝하기

이 부분이 가장 시간이 많이 들고 힘든 부분이다. Kp, Ki, Kd를 튜닝하는데에는 많은 다양한 방법이 있지만, 그 중 몇몇만 소개하려 한다.
PID 상수를 튜닝하는 방법은 컴퓨터 프로그램을 이용할 수도 있고, 수학적으로 계산할 수도 있고, 직접 튜닝할 수도 있다.
튜닝할 때에는 최대한 모든 error와 speed를 관찰하길 권장한다. 그래야 로봇이 얼마나 target에 가까워 졌는지, 얼마나 더 변화시켜야 하는지를 알 수 있을 것이다. 디버거나 모니터링 도구를 이용하길 바란다.

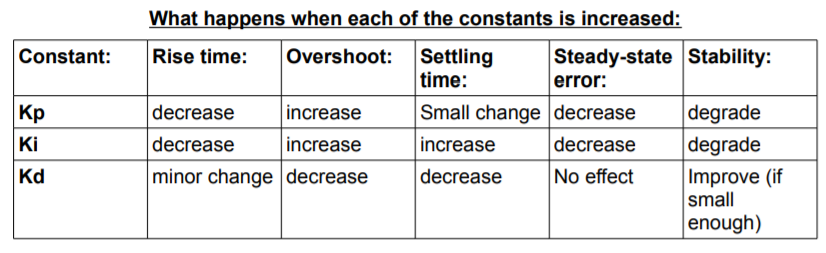
무엇보다도 PID Controller를 튜닝하려면 그 규칙을 아는게 중요하다. 각각의 상수값이 증가했을때 어떠한 효과가 발생하는지는 아래 표를 참고하면 된다.

• Rise time - 시작점부터 목적지까지 걸리는 시간
• Overshoot - 과하게 변화하는 정도; error보다 과하게 변화한 정도
• Settling time - 변화를 만났을때 다시 안정화되기까지 걸리는 시간
• Steady-state error - 안정화상태에서의 error
• Stability - 속도의 "부드러운 정도"
  

Manual Tuning

Manual Tuning은 수학적인 것 필요없이 직접 손으로 튜닝하는 방법을 말한다. 이렇게 하면 시간적으로는 비효율적일 수 있지만 직접 각각의 상수값을 조절하며 각 상수값의 변화에 따라 어떤 현상이 발생하는지 알 수 있다.
반면에 수학적으로 계산하여 튜닝을 하게되면 실제로 적용해보기 전까지는 어떤 일이 발생할 지 알 수 없다. 이론과 실전은 다르기 때문이다.
상수값을 튜닝하는 방법은 아래와 같다.

• 1. Kp, Ki, Kd를 0으로 맞춘다. 이렇게 하면 PID를 비활성화하는 효과를 얻는다.
• 2. Error가 충분히 작으며, 동시에 목적지에 충분히 빨리 도착할 때까지 Kp 값을 증가시킨다.
• 3. Overshoot가 충분히 작아질때까지 Kd를 증가시킨다. 단, 너무 많이 증가시키게 되면 오히려 overshoot가 발생할 수 있기에 주의해야한다.
• 4. 남은 error들이 모두 없어질때까지 Ki를 증가시킨다. 이때 Ki는 정말 작은 수부터 대입시켜 가며 테스트해야한다.
     (0.0001보다 더 작아질 수도 있다!)
• 5. 상수 값 튜닝 규칙을 참고하여 상수 값을 추가로 더 조절하면 최고의 성능을 얻을 수 있을 것이다.