이번 시간에는 지금까지 배웠던 개념들로 실제로 Authentication Protocol 들이 어떻게 동작하는가에 대해서 알아보려 합니다.

계속 이야기 했지만 Authentication 이란 무엇일까요? 한국말로 '인증' 이라고 합니다. 개체의 정체성을 입증하는 과정을 의미합니다. 정말 간단하게 얘기해서 나는 나 맞어! 너는 너 맞어? 등을 하는 거지요. 인증은 상호간에 이루어지는 만큼 one-way(단방향) 이 있고, two-way(양방향)이 있습니다.

단방향의 예시로는 우리가 사용하는 스마트폰 잠금해제가 있는데요. 우리는 스마트폰을 열기 위해 주인인 나를 인증합니다. 비밀번호, 패턴, 지문, 홍채 등등의 방식으로요. 스마트폰이 우리를 인증하는 단계이지만, 사실 우리는 스마트폰을 인증하려 하지 않습니다. 이 폰이 진짜 내 폰인지를요. (물론 실제로는 굳이 할 필요가 없어서 그렇지만요🤣)

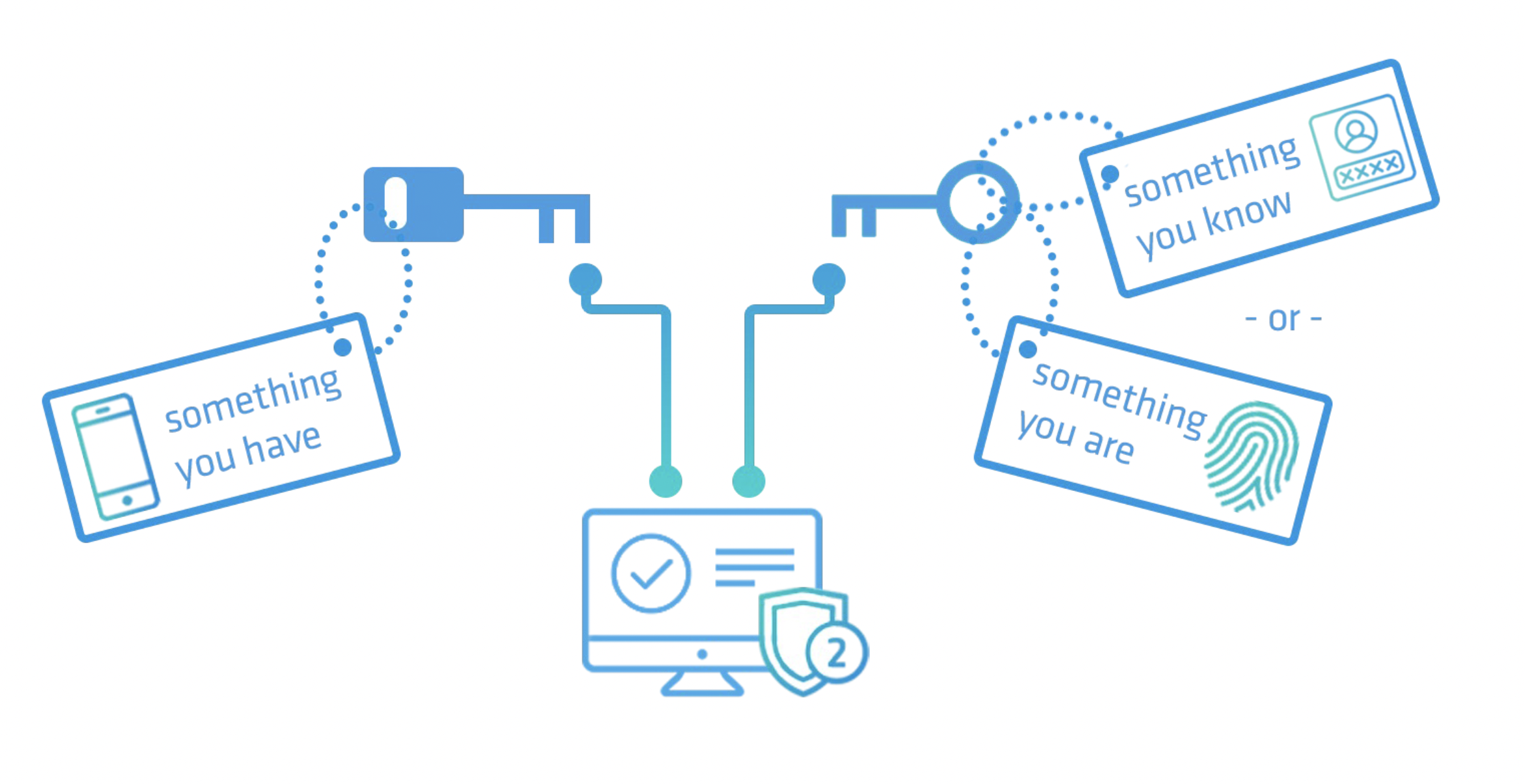
그렇다면 이러한 인증은 왜 중요할까요? 인터넷 상에서는 서로에 대해 실제로는 모르는 관계이기 때문입니다. 네트워크로 연결된 상대가 진짜 내가 생각하는 상대방인지 직접 확인할 수가 없기 때문에 인증은 필수입니다. 인증에는 다음과 같은 3가지가 필요합니다.

• What You Know
  서로 아는 것을 통해서 인증을 할 수 있습니다. 예시로 비밀번호가 있습니다.
• What You Have
  가지고 있는 것을 통해서 인증을 할 수 있습니다. 예시로 여권이 있습니다.
• Who You Are
  나 자신을 나타내는 것을 통해서 인증을 할 수 있습니다. 예시로 홍채, 지문이 있습니다.

우리는 이 중에서 What You Know, 그 중에서도 우리에게 가장 인숙한 패스워드 에 대해서 알아보려 합니다.

Password

패스워드는 인증을 위해 서로 공유되는 값입니다. 기억하기는 쉽지만, 추측하기에는 어려운 값이 이상적이라고 할 수 있겠습니다. 사용자가 정하고 서버의 데이터베이스에 저장되는 것이지요. 강력한 패스워드라고 한다면 길이가 길고 소문자, 대문자, 숫자, 특수문자 등 하나의 패스워드 문자가 될 수 있는 후보군이 많아야 합니다. 또한 Dictionary 에 없는 값이어야 하는데요. 뒤에서 설명드리겠습니다.

위의 그림이 정말 가장 naive 한 password-based authentication 을 그림으로 표현한 것입니다. 인증을 위해 Alice 가 Bob 에게 자신의 비밀번호를 보내고 있습니다. 그런데 이런식으로 평문으로 보내면 당연히 안되겠죠? Eavesdropping(도청) 위험에 빠지니까요. 그러니 우리는 암호화를 해야할 겁니다. 암호화를 하려면 key sharing 이 필요하겠구요. key sharing 을 하기 전에는 서로에 대한 인증이 필수임을 이미 설명드린 바 있습니다. 잠깐만요...그렇다면 인증을 위해 인증이 필요한 어처구니 없는 상황이 만들어지네요?

그래서 우리는 Hash 를 사용할 겁니다! One-way 이기 때문에 누군가 도청하더라도 비밀번호를 알 수 없습니다. (정확히는 거의 불가능합니다.)

패스워드를 깨는 것, 즉 Cracking 에는 크게 Online Guessing, Offline Guessing 이 있습니다.

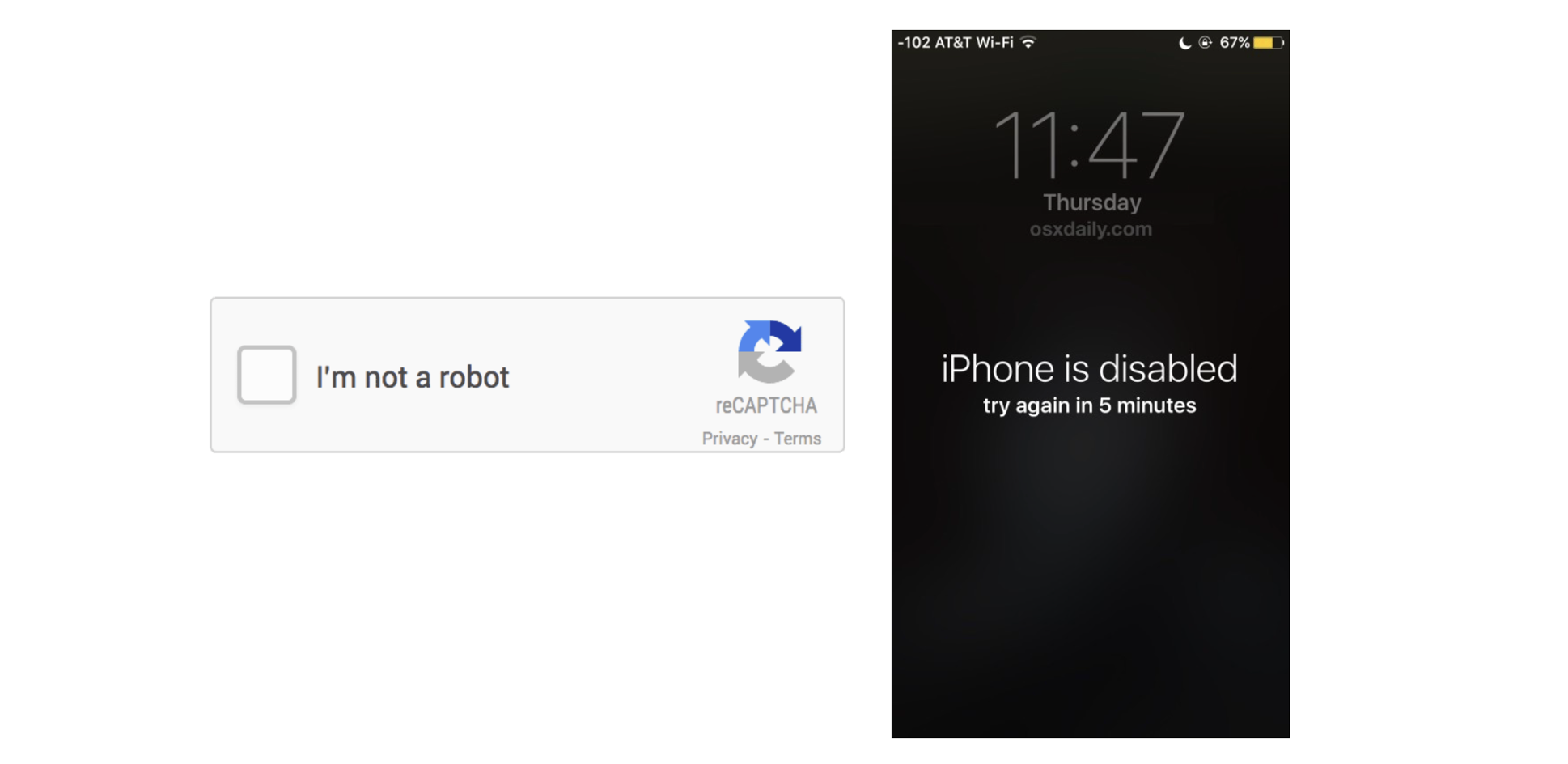
Online Guessing 은 실제 패스워드를 입력하는 곳에서(online) 패스워드를 소위 말해 때려 맞춰보는 것입니다. 계속해서 패스워드를 시도해 보는 것입니다. 해결법은 의외로 간단합니다. 비밀번호를 계속해서 시도하다가 실패가 일정 이상이 되면 뭔가 잠시 뒤에 시도한다거나 막힌다거나 하는 등 락이 걸리는 경험, 모두 있으시죠? 이런 식으로 시도 횟수 자체를 아예 제한해 버리는 겁니다. 아이폰은 심지어 어느 횟수를 초과하면 자동으로 공장 초기화를 진행한다고 합니다...😬 또 이런 시도를 사람이 하지 않고 프로그램을 돌려서 자동으로 하는 것을 막기 위해 모두들 한 번쯤 해본 CAPCHA 를 쓰기도 합니다.

Offline Guessing 은 내 컴퓨터 내에서(offline) 가지고 있는 패스워드의 해시 값을 이용해 패스워드를 추측해 보는 방법입니다. 아까 말씀드렸다시피 시스템은 패스워드의 해시 값을 취급합니다. Unix 에서도 과거에는 /etc/passwd 위치에 패스워드를 저장해 두었습니다. 하지만 지금은 이름은 바뀌지 않고 그 용도가 운영체제의 사용자 정보를 저장하는 데 사용되고, 패스워드는 /etc/shadow 에 그 해시값들이 저장되어 있습니다.

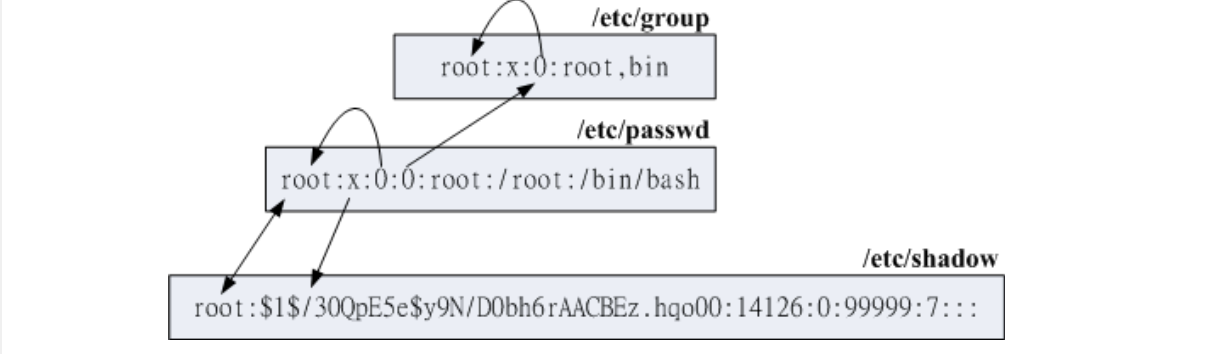
맨 아래와 같은 값이 저장되어 있습니다. 맨 앞에 root 가 써있는 것을 보면 이 값은 오직 root 만이 읽을 수 있다는 것을 알 수 있습니다. 그 뒤에 나오는 필드는 해시 알고리즘의 ID 를 뜻합니다. 1은 MD5 를 뜻합니다. 추가적으로 6은 SHA-512 을 의미합니다. 뒤에 나오는 필드는 salt 값을 뜻합니다. 이게 무엇인지는 뒤에서 설명드리겠습니다. 그리고 뒤에 나오는 필드 값이 진짜 해시 값을 나타내는 것입니다.

결국 이 Guessing 과정은 필연적으로 Brute-Force 방식입니다. 그런데 이렇게 되면 패스워드가 단 10 자리라 하더라도 경우의 수가 무려 $128^{10}$ 가지가 됩니다. 그래서 사용하는 것이 바로 Dictionary 입니다. 해시 값을 미리 만들어놓으면 비교만 하는 것은 1000배 이상 빠릅니다. 이를 이용해 사전에 패스워드 후보군들을 선정해 해시 값들을 모아놓은 것이 바로 Dictionary 입니다. 이러한 Dictionary Attack 을 막기 위해 같은 패스워드여도 그 때 그 때 다른 해시 값을 만들기 위해 도입한 IV 가 바로 Salt 인 겁니다.

Rainbow Table

그럼 Dictionary 를 직접 사람이 다 계산해서 작성해야 할까요? 만들어 놓아야 하는 값들이 산더미기 때문에 그건 사실상 불가능합니다. 컴퓨터가 알고리즘을 통해 많은 값들을 자동적으로 만들어주어야 할테죠. 그렇게 만들어진 테이블을 Rainbow Table 이라 합니다.

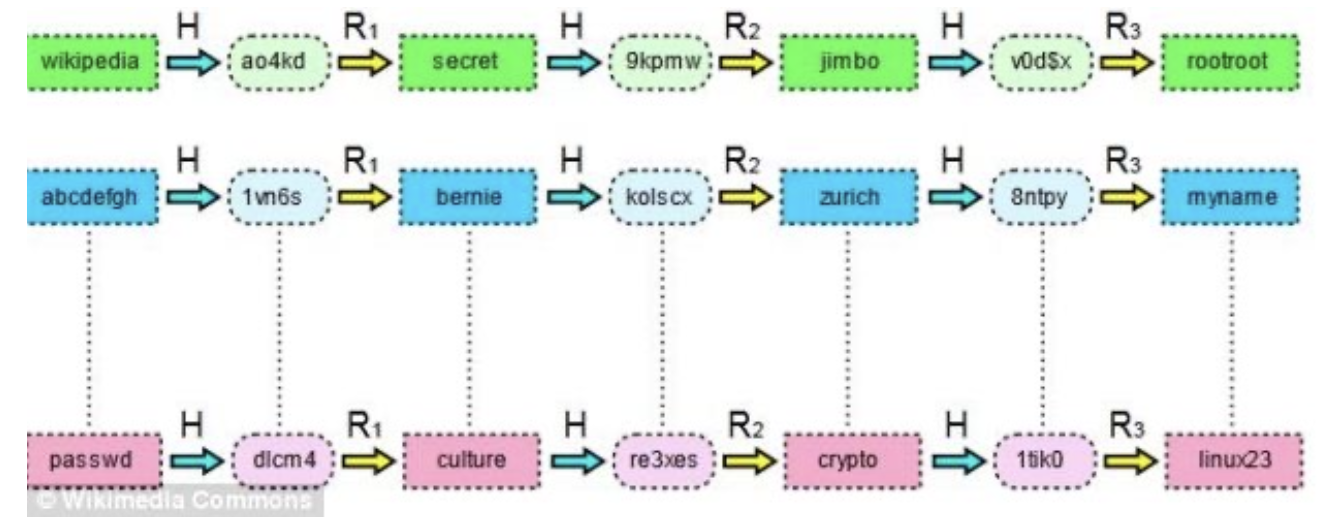
맨 먼저 패스워드 값들의 리스트들을 최대한 많이 작성합니다. 그리고 이것들로 해시값들을 만들어 두는 겁니다. 그리고 이 값들로 cracking 을 시도해 보는 겁니다. 여기서 바로 나온다면 그야 말로 대박이지만, 아닐 확률이 더 높겠죠? 그 때 이 해시값을 평문으로 바꾸어주는 Reduction Function 을 사용하는 것입니다. 그렇게 만들어진 평문으로 새로운 패스워드 후보군들이 나오고 이들의 해시값으로 다시 한 번 cracking 을 시도하고 이를 계속해서 반복합니다. Reduction 함수는 역해시 함수가 아닙니다. 그럴 수도 없습니다. 그저 각각의 방식을 통해 해시 값을 (의미를 두지 않고) 새로운 평문 값으로 만들어줄 뿐입니다. 그러나, 조금 더 그럴듯한 평문(패스워드) 값을 뽑아내는 Reduction 함수야 말로 돈이 되는 함수인 겁니다.🤑

Cryptographic Authentication

그렇다면 차라리 아예 패스워드가 아닌 다른 방식으로 인증을 할 수는 없을까요? 있습니다. 바로 이전에 공부하였던 Cryptography 를 활용하는 것입니다.

보안 프로토콜의 필수 요소에는 다음과 같은 두 가지 필수조건이 존재합니다.

• 상호 인증
• 비밀 키 공유

앞선 해시를 이용한 패스워드 방식은 Unix 운영체제에서 사용되던 것처럼 하나의 컴퓨터 내에서는 더할 나위 없이 좋은 방식입니다. 그렇지만 네트워크로 넘어가는 순간Replay 문제가 발생하게 됩니다. 실제로 패스워드가 다르더라도 같은 해시값이라면 패스워드가 맞다고 판단하게 되버리는 것이지요. 공격자가 중간에 이 해시값을 알 수 있기 때문에 이를 통해 패스워드 값을 알 수는 없지만, 굳이 모르더라도 사용자로 위장할 수 있습니다.

결국 해시 값이 고정되어 있는 것이 문제입니다. 이를 막기 위해 challenge-response 를 사용합니다. 매번 새로운 challenge 를 주고 거기에 대한 response 를 받으면 이전 것을 다시 사용하는 replay 는 할 수 없게 됩니다. 이 때 challenge 로 주는 값을 Nonce(number used once) 라고 합니다. 이제 이 내용을 시작으로 본격적으로 들어가기 전에 몇몇 표기를 약속하고 가겠습니다.

• $E[R]_{Apriv}$
  $A$ 의 private key로 $R$ 을 Encrypt 한 값
• $E[R]_{Apub}$
  $A$ 의 public key로 $R$ 을 Encrypt 한 값
• $F(K,R)$
  비밀 키 $K$ 로 $R$ 을 Encrypt 하는 함수
  *$E[C]_K$
  비밀 키 $K$ 로 $C$ 를 Encrypt 한 값

One-way Authenticatoin

가장 기본적인 challenge-response 예시입니다. Bob이 I'm Alice 라고 하는 Alice 를 인증하기 위해 challenge, 즉 Nonce 값 $R$ 을 줍니다. 그러면 Alice 는 서로 공유하고 있는 있는 $K$ 를 이용해 거기에 알맞은 response를 보내는 것입니다. 공격자는 공유키 $K$ 를 모르기 때문에 패킷을 뺐어 인증을 방해하고 그럴 수는 있더라도 정작 하고 싶은 위장은 불가능합니다. 그렇다면 이 방식의 문제는 뭐가 있을까요?

일단 먼저, symmetric 방식이기 때문에 부인 방지가 불가능하겠군요. Bob 도 K 를 가지고 있기 때문에 Alice 가 Bob 이 했다고 할 수 있을 테니까요. 그리고 이와 같은 방식은 상호적이지 않습니다. 오직 Alice 만 Bob 에게 인증하는 one-way 방식이니까요.

공격자는 중간에 평문으로 날아가기에 $R$ 도 알고 $F$ 는 공개되었으니 알고, 또 평문으로 날아가는 $F(K,R)$ 도 알 수 있습니다. 그러면 공격자는 $K$ 값을 Brute-Force 하면서 offline guessing 공격을 시도해볼 수 있는 겁니다. 또한 challenge 를 모아 두면 새로운 challenge 가 재사용 됬을 때 바로 replay 공격도 가능해지게 됩니다.

이 문제를 해결하기 위해 Public Key 를 사용해 보자는 겁니다.

첫 번째, 두 번째는 전과 같지만 세 번째서 $R$ 을 Alice 의 private key 로 암호화해서 줍니다. 그러면 Bob 은 이를 Alice 의 public key 로 풀어서 실제 $R$ 인지를 확인하는 것입니다.

그럼 이제 앞의 4가지 문제점을 살펴봅시다. Asymmetric, 즉 public-key 방식이기 때문에 이제 부인 방지가 가능해집니다. 그리고 비밀 키가 없이 오직 private key 이기 때문에 offline guessing 또한 하기 어려워질 겁니다.

그러나 여전히 상호적인 인증 방식이 아닌 one-way 방식입니다. 이 또한 마찬가지로 challenge 가 재사용되면 replay 를 막을 수도 없을 겁니다. 그리고 가장 치명적으로는 두 번째에 날아가는 저 $R$ 을 조작할 수 있다는 것입니다. Alice 는 무엇이든 그것을 private-key 로 암호화, 즉 디지털 서명을 하기 때문에 예를 들어 $R$ 을 Alice 가 빚을 졌다는 내용을 보내면 그에 대한 Alice 의 디지털 서명을 가지어 실제로 효력이 발생할 수 있다는 것이지요.

그렇기 때문에 이제 반대로 Bob이 $R$ 을 public key 로 암호화해서 주고 Alice 는 그것을 private key 로 풀어 실제 $R$ 을 리턴하는 방식을 취해보자 이겁니다. 하지만 이 때도 두 번째 패킷을 조작하여 공격자는 Alice 의 private key로 풀고 싶은 것들을 풀게 할 수 있게 됩니다.

하지만 이 방식의 진짜 문제는 바로 그 무섭다는 DoS 공격으로 이어질 수 있다는 것입니다. 공격자는 그저 I'm Alice 와 같이 간단한 평문 패킷을 Bob에게 보내지만, Bob 은 그 때 마다 $R$ 을 만들고 그 무거운 asymmetric encryption 을 하게끔 만들 수 있는 것이지요...😫 이와 같이 DoS 공격은 보내는 사람(공격자)는 쉽고 가볍고, 받는 사람(피해자)는 어렵고 무거워야 의미가 있는 것입니다.

Mutual Authentication

이제는 one-way 가 아닌, 상호적인 mutual 방식으로 다시 처음부터 프로토콜을 짜봅시다. 먼저, 다시 $K$ 를 이용한 challenge-response 방식을 양방향으로 진행하는 것을 그림으로 표현한 것입니다.

Alice 는 자신이 Alice 임을 보내는 동시에 challenge $R2$ 를 보냅니다. 그러면 Bob 은 이에 대해 reponse 인 $F(K,R2)$ 를 보내면서 새로운 challenge $R1$ 을 보냅니다. 마지막으로 Alice 가 이에 대해 reponse 를 보내면 서로를 인증할 수 있게 되는 겁니다.

이 방식이 의미가 있을 수 있는 이유는 위와 같이 공격자가 Bob 의 challenge $R1$ 에 대한 response $F(K,R1)$ 를 몰라 보낼 수 없기 때문입니다. $K$ 를 모르기 때문이죠. 그렇다면 아래와 같이 한다면 어떨까요?

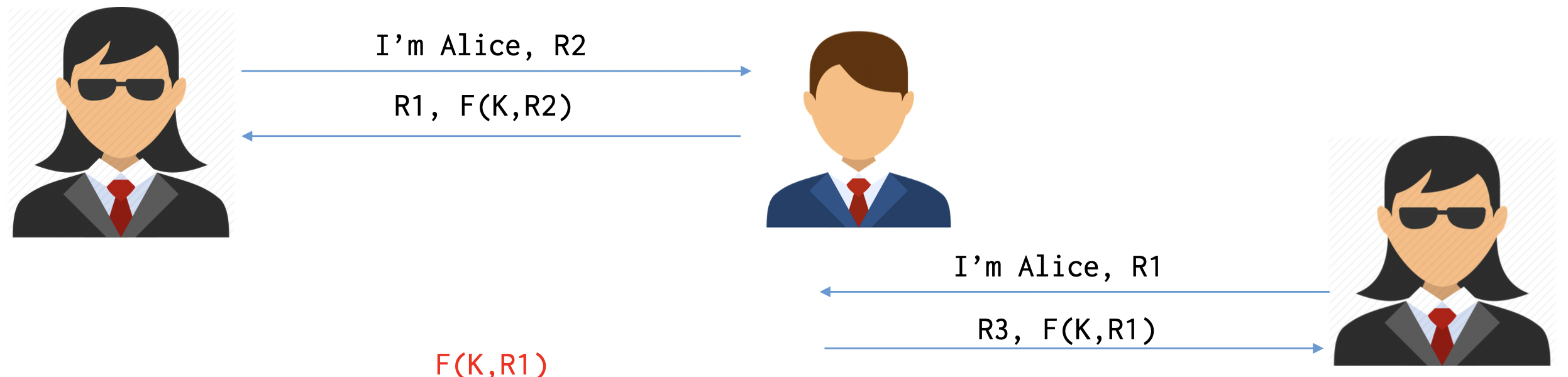
두 번째 패킷으로 $R1$ 을 받은 다음에, 공격자가 새로운 세션을 열어 Bob 에게 이 $R1$ 을 challenge 로써 부여할 수 있겠지요? 그러면 Bob 은 아무것도 모르고 이에 대한 response 인 $F(K,R1)$ 을 먼저 계산해서 보내줄 겁니다. 이를 공격자는 다시 이전 세션으로 돌아와 Bob 에게 $R1$ 에 대한 response 로써 보낼 수 있는 것이죠. 이 공격을 Reflection Attack 이라고 합니다.

이 공격이 통하는 이유는 항상 같은 $K$ 를 쓴다는 점입니다. 그렇기 때문에 이를 해결하기 위해서 각 세션마다 서로 다른 key $K$ 를 쓰면 됩니다. 이 정도면 꽤 괜찮은 프로토콜이 완성되어 가고 있지요? 그 다음에 이제 Public Key 방식을 알아보도록 합시다.

이 전에 보여드렸던 public-key 방식을 그저 상호적으로 재구성한 그림입니다. private key 로 암호화하면 해서는 안 될 것에 디지털 서명을 해버리는 너무나 치명적 문제가 있었기 때문에 public key 로 암호화합니다. 이렇게 되면 DoS 공격은 어느 정도 해결이 될 겁니다. Alice 는 갑자기 자신이 challenge 를 준 적이 없는 $R2$ 가 들어오니까요. 하지만 여전히 두 번째를 끊어 Alice 가 복호화를 하게끔 하는 replay 공격은 통한다는 단점이 있습니다. 또한, 결국 public-key 방식은 근본적으로 이 public key 가 상대방의 public key 가 맞는지에 대한 유효성을 검증하기 힘든 문제가 존재합니다.

Encrypted Key Exchange(EKE)

그래서 나온 것이 거의 완성된 프로토콜인 EKE 입니다. 핵심은 이전에 공부하였던 Diffie-Hellman 을 사용하자는 것입니다.

먼저, Alice 는 자신의 private key 인 $a$ 로 public key 인 $g^a \ mod \ p$ 를 만들어 Bob 에게 줍니다. 그러나 여기서 핵심은 이를 Alice 의 패스워드의 해시값인 $W$ 로 암호화하여 보낸다는 것입니다. 이를 통해서 바로 서로 public key 를 인증할 수 있게 되는 것입니다. 그 다음엔 Bob 이 자신의 public key 인 $g^b \ mod \ p$ 를 보내면서 뒤에 $C1$ 을 덧붙여서 보냅니다. 이 값을 향후 만들어질 서로의 공유 키(세션 키) 인 $K$ 를 마지막으로 확인하고자 보내는 값입니다.

그렇다면 이 두 번째 이후에 서로가 알고 있는 $W$ 값이 맞다면 같은 세션 키인 $K = g^{ab} \ mod \ p$ 를 가지게 될 것입니다. 그 뒤에 Alice 는 $C1$ 과 $C2$ 를 $K$ 로 암호화하여 보냅니다. 그러면 Bob 이 이를 $K$ 로 풀어봐서 자신이 보낸 $C1$ 과 맞는지 확인함으로써 Alice 의 $K$ 를 인증할 수 있습니다. 그러면 Bob 도 다시 $C2$ 를 $K$ 로 암호화해서 보내면서 Alice 또한 Bob 의 $K$ 를 인증하면서 모든 인증을 마치게 됩니다.

이 프로토콜은 인증과 동시에 세션키를 만들어 주기까지 한다는 좋은 장점을 가집니다. 즉, 보안 프로토콜의 두 가지 요소인 상호 인증과 키 공유를 모두 충족시키는 것이지요. 또한, 세션 별로 키를 만들기 때문에 아까 설명드렸던 Reflection Attack 을 해결하기도 합니다. 그리고 복호화를 해서 넘겨주는 과정없이 암호화만 진행하기 때문에 Replay 공격을 해야할 이유도 사라집니다. 그뿐일까요? 공격자는 $E[g^a \ mod \ p]_W$ 는 알더라도 정작 $g^a \ mod \ p$ 는 모르기 때문에 offline guessing 또한 할 수가 없습니다. 이 정도면 거의 완벽한 프로토콜이라고 해도 무방하곘죠.😁

Perfect Forward Secrecy(PFS)

하지만 정말 완전한 보안을 위해서는 생각해야 할 것이 하나 더 있습니다. Alice 과 공유키 $K$ 를 이용해서 메시지를 암호화한 암호문을 공격자는 복호화할 수 없습니다. 하지만 Brute-Force 를 하면 언젠가는 풀리게 됩니다. 그래서 공격자가 이 암호문을 저장해놓고 공격을 돌려놓으면 예전에 했던 암호문들은 결국 다 풀리게 되는 겁니다. 우리는 이것을 원치 않겠지요. 아무리 예전 것이더라도 풀려서는 안되는 것입니다.

결국 공격자가 나중에 $K$ 를 알더라도 복호화에 사용할 수 없어야 할 겁니다. 피해를 최소화하기 위해 우리는 항상 $K$ 를 쓰는 것이 아니라 그때 그때 다른 값을 써야합니다. 즉, $K$ 에 파생된 값들을 하나씩 써가는 겁니다.

이 때 유용한 방법이 또 Hash 를 사용하는 것입니다. $K$ 의 해시 값으로 $SK_1$ 파생시켜 사용했다고 합시다. 해시의 one-way 때문에 훗날 $SK_1$ 을 알게 되더라도 $K$ 를 알지 못합니다. 또한 $SK_2, SK_3, SK_4, ...$ 또한 알 수가 없는 것이지요. 이 $SK$ 값을 10초에 한 번씩, 20초에 한 번씩 등 정기적으로 업데이트합니다. 또한 $K$ 또한 지속적으로 바뀌는 것이 좋겠지요. 하지만 만약 $K$ 를 알아낸다면 $SK$ 는 알아낼 수 있기 때문에 $K$ 또한 volatile 하게 만들어야 할 겁니다.

방법은 Ephemeral Diffie-Hellman 입니다. 즉 Diffie-Hellman 을 통해 세션 키를 만드는 과정에서 Alice 와 Bob 이 각자의 private key 인 $a$ 와 $b$ 를 한 번만 사용하고 버리는 겁니다. 공격자가 public key 인 $g^a \ mod \ p$ 를 안다고 해도 $b$ 를 버려서 이를 알 수 없기 때문에 키인 $g^{ab} mod \ p$ 를 알 수가 없는 것이죠. 전수 조사를 300~400 년을 해야할 겁니다. 이 방식 또한 거의 완전하다고 볼 수 있습니다.