문제 📕

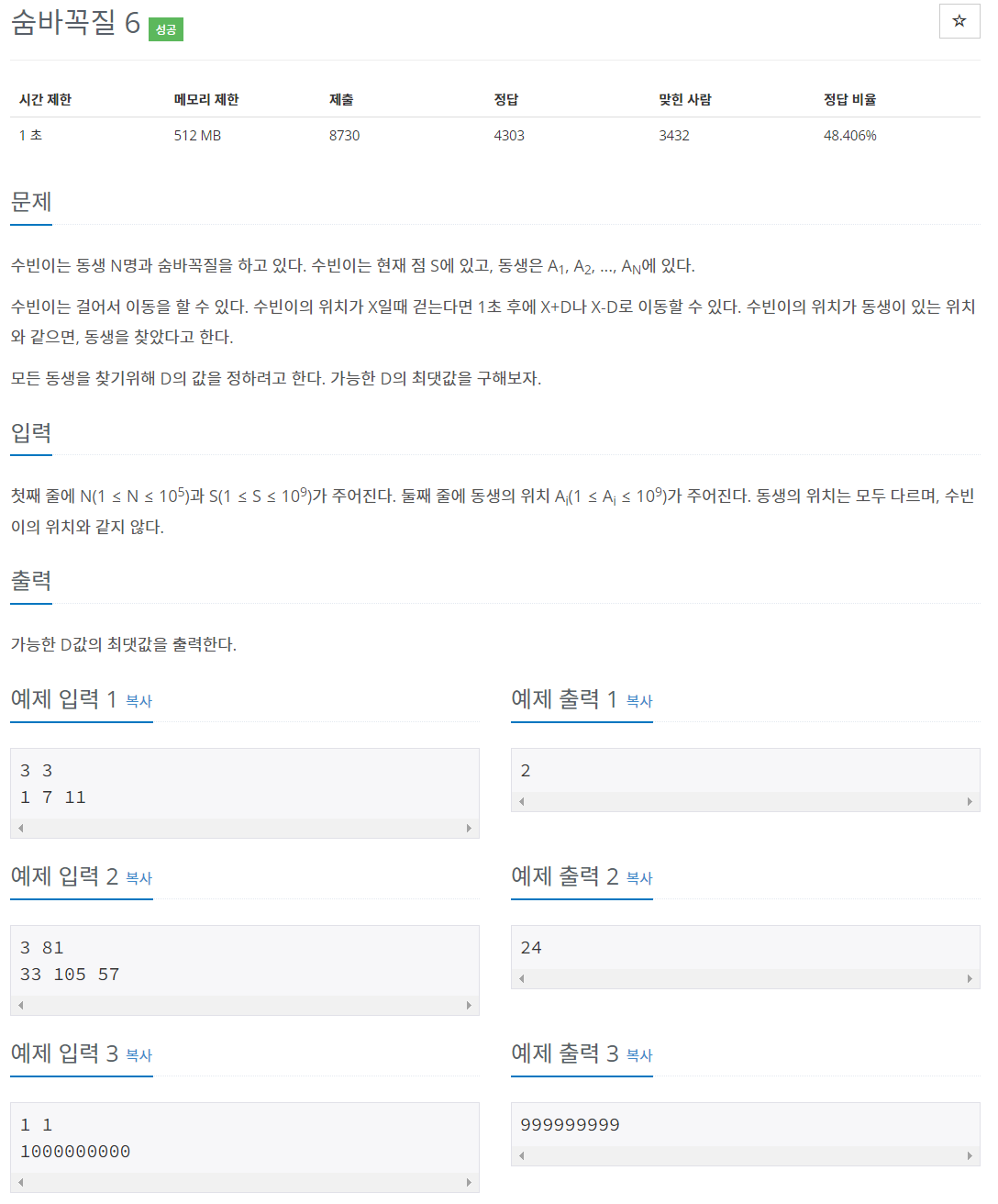
수빈이는 동생 N명과 숨바꼭질을 하고 있다. 수빈이는 현재 점 S에 있고, 동생은 A1, A2, ..., AN에 있다.

수빈이는 걸어서 이동을 할 수 있다. 수빈이의 위치가 X일때 걷는다면 1초 후에 X+D나 X-D로 이동할 수 있다. 수빈이의 위치가 동생이 있는 위치와 같으면, 동생을 찾았다고 한다.

모든 동생을 찾기위해 D의 값을 정하려고 한다. 가능한 D의 최댓값을 구해보자.

(https://www.acmicpc.net/problem/17087)

접근 방법 🧐

어머 이름이 나와 같은 '수빈' 이라 바로 문제한테 내적 친밀감을 느꼈다 🤣

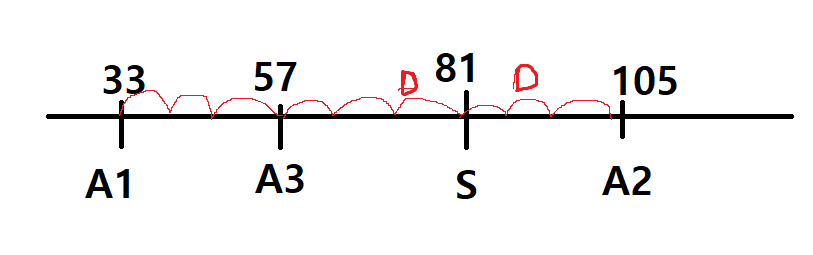
예제 입력2를 바탕으로 만든 그림이다.
1초 후에 D만큼 이동할 수 있는데, D를 하나의 발걸음이라고 보면 이런식으로 수빈이는 이동할 것이다.

문제를 읽으며 든 생각을 순서대로 써보자면,

1. X + D 나 X - D로 이동할 수 있으니, 절댓값을 사용해야겠네 (Math.abs)
2. 가능한 D의 최댓값 을 구해야하니 "최대공약수"를 사용해야하네 (유클리드 호제법)

유클리드 호제법

검색해보면 아주 잘 설명해주신 분들이 많아서 내가 이해한 대로만 간단하게 써놓자면,

숫자 A 숫자 B가 있습니다.

A, B의 최대공약수는 r = A mod B의 값인 r과의 최대공약수와 같습니다.

- 나머지가 없다는 것은 공통된 약수로 떨어진다는 의미

예를 들어,
A = 69, B = 42이다
여기서 GCD는 최대공약수이다.

GCD(69,42) r = 27
GCD(42,27) r = 15
GCD(27,15) r = 12
GCD(15,12) r = 3
GCD(12,3) r = 0

최대공약수는 3

내가 쓴 코드 ✍️

import java.io.*;
import java.util.*;


public class Main {

	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringTokenizer st = new StringTokenizer(br.readLine());
		
		int n = Integer.parseInt(st.nextToken());
		int s = Integer.parseInt(st.nextToken());
		int[] dList = new int[n];
		st = new StringTokenizer(br.readLine());
		for(int i=0;i<n;i++) {
			dList[i] = Math.abs(s - Integer.parseInt(st.nextToken()));
		}
		
		int result = dList[0];
		for(int i=1;i<n;i++) {
			result = gcd(result, dList[i]);
		}
		
		bw.write(result+"");
		bw.flush();
		bw.close();
	}
	
	public static int gcd(int a, int b) {
		if(b == 0)
			return a;
		return gcd(b, a % b);
	}

}