알고리즘 기초 3주차 - 분할정복 (3)

원종운·2020년 4월 14일

2.4 빠른정렬(Quicksort)

: 기준 원소(pivot)를 선정하여 기준원소보다 작은 원소는 모두 왼쪽 배열로, 기준원소보다는 크거나 같은 원소는 모두 오른쪽 배열로 가도록 분할한다. 이렇게 분할한 배열을 각각 재귀 호출로 정렬하여 합병하는 방식.

절대적으로 가장 빠른 정렬 알고리즘이라고 할 수 없음.
"분할교환정렬(partition exchange sort)" 라고 부르는게 더 정확함.

문제: n개의 정수를 비내림차순으로 정렬
입력: 정수 n >0, 크기가 n인 배열 S[1..n]
출력: 비내림차순으로 정렬된 배열 S[1..n]

void quicksort(index low, index high) {
  index pivotpoint;
  
  if (high > low) {
    partition(low, high, pivotpoint);
    quicksort(low, pivotpoint - 1);
    quicksort(pivotpoint + 1, high);
  }
}

partition(분할 알고리즘)

문제: 빠른 정렬을 하기 위해서 배열 S를 둘로 쪼갠다.
입력: 첨자 low, high
출력: 첨자 low에서 high까지의 S의 부분배열의 기준점(pivotpoint)

void partition(index low, index high, index& pivotpoint) {
  index i, j;
  keytype pivotitem;
  
  pivotitem = S[low];
  j = low;
  
  for(i = low + 1; i <= high, i++) {
     if (S[i] < pivotitem) {
       j++;
       exchange S[i] and S[j];
     }
  }
  
  pivotpoint = j;
  exchange S[low] and S[pivotpoint]
}

partition(분할 알고리즘)의 분석

단위연산: S[i]와 pivotitem과의 비교
입력크기: 부분배열이 가지고 있는 항목의 수, n = high - low + 1
분석: 배열의 첫번째 항목만 제외하고 모든 항목을 한번씩 비교하므로 T(n) = n - 1;

Quicksort의 분석 - 최악의 경우

단위연산: 분할 알고리즘의 S[i]와 pivotitem 과의 비교
입력크기: 배열이 S가 가지고 있는 항목의 수, n
분석:
최악 경우 - 비내림차순으로 정렬이 되어 있는 배열을 정렬하는 경우
T(n) = T(0) + T(n-1) + n - 1 (partition 알고리즘), T(0) = 0
T(n) = n(n-1)/2
-> 이미 정렬이 되어 있는 경우 빠른정렬 알고리즘의 시간복잡도: theta(n2)

2.5 행렬 곱셈(Matrix Multiplication)

문제: nxn 크기의 행렬 곱을 구하시오.
입력: 양수 n, nxn 크기의 행렬 A와 B
출력: 행렬 A와 행렬 B의 곱인 C

void matrixmult(int n, const number A[][], const number B[][], number C[][]) {
  index i, j, k;
  for(i = 1; i <= n; i++)
    for(j = 1; j <= n; j++) {
      C[i][j] = 0;
      for (k = 1; k <= n; k++)
        C[i][j] = C[i][j] = A[i][k] * B[k][j]
    }
}

행렬 곱셈의 시간복잡도 분석

단위연산: 가장 안쪽의 루프에 있는 곱셈 연산
입력크기: 행과 열의 수 n

모든 경우 시간복갑도 분석: 총 곱셈의 횟수 : T(n) = nnn = n^3 theta(n3)

2 x 2 행렬곱셈 : 쉬트라센의 방법

문제: 두 2 x 2 행렬 A와 B의 곱 C

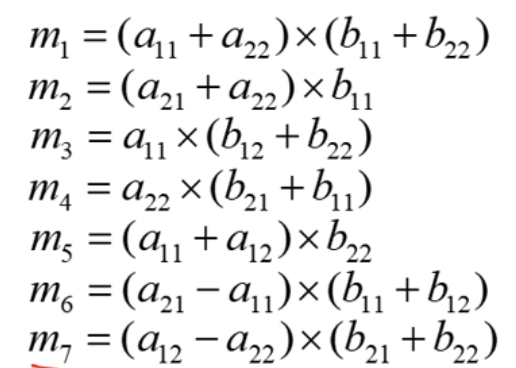
쉬트라센의 방법 시간복잡도 분석

이전의 방법의 경우는 8번의 곱셈과 4번의 덧셈, 쉬트라쎈의 방법은 7번의 곱셈과 18번의 덧셈/뺄셈을 필요
언뜻 봐서는 전혀 좋아지지 않으나 행렬의 크기가 커지면 쉬트라센의 방법의 가치가 들어난다.

문제: n이 2k이고, 각 행렬을 4개의 부분행렬(submatrix)로 나눈다고 가정하자. 두 nxn 행렬 A와 B의 곱 C

쉬트라쎈의 해

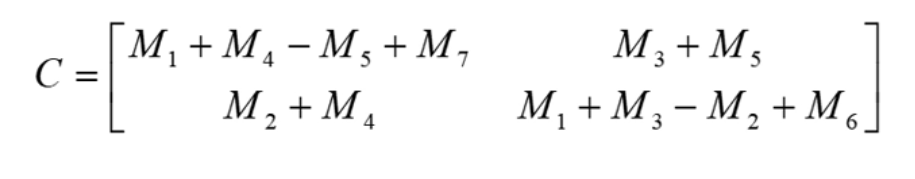
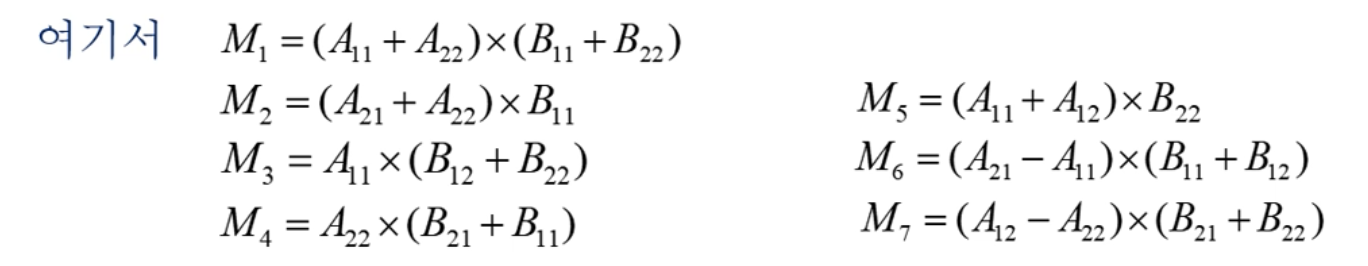
문제: n이 2k일 때, n x n 크기의 두 행렬의 곱을 구하시오.
입력: 정수 n, n x n 크기의 행렬 A와 B
출력 행렬 A와 B의 곱 C

void strassen(int n, n*n_matrix A, n*n matrix B, n*n_matrix& C) {
 if (n <= threshold)
   표준 알고리즘을 사용하여 계산
 else {
   A를 4개의 부분행렬로 분할
   B를 4개의 부분행렬로 분할
   strassen(n/2, A11 + A12, B11 + B22, M1);
   ...
   strasse(n/2, ..., ... , M7);
   // M1 ~ M7으로부터 C11, C12, C21, C22를 구성한다.
 }
}