그래프란
- 그래프(G)란 정점들과 그 정점들을 잇는 간선들을 모아둔 비선형 자료구조입니다.
- G = (V, E) [ V : 정점들의 집합, E : 간선들의 집합 ]
기본적인 용어
1. 오일러 경로
무향 또는 유향 그래프의 모든 간선을 한번씩만 방문하는 경로
2. 해밀턴 경로
무향 또는 유향 그래프의 모든 정점을 한번씩만 방문하는 경로
3. 해밀턴 순환(싸이클)
해밀턴 경로 중 순환(싸이클)을 형성하는 경로
구현 방법
1. 인접 행렬
2. 인접 리스트
그래프 순회
- 그래프 탐색이라고도 불리우며, 그래프의 각 정점을 방문하는 방법
- 탐색 방법에는 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 있으며, 일반적으로 DFS를
주로 사용한다.
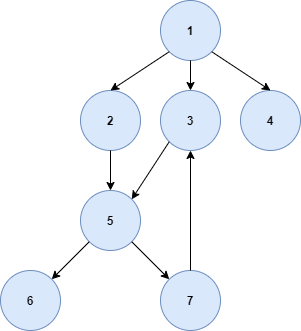
0. 그래프 표현 - 딕셔너리 사용
- 키를 정점, 값을 정점과 인접한 정점들을 집합으로 할당하는 방식을 사용
- 그래프 코드
graph = { 1: set([2, 3, 4]), 2: set([5]), 3: set([5]), 4: set([]), 5: set([6, 7]), 6: set([]), 7: set([3]), }
- 그래프 그림
1. 깊이 우선 탐색(DFS, Depth First Search)
- 시작 정점(일반적으로 루트 정점)에서 시작하여, 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
- 주로 스택 또는 재귀로 구현하며, 백트래킹 작업에 뛰어난 효용을 보입니다.
1) 스택을 이용하여 구현
- python에서는 별도로 Stack 자료구조를 지원하지 않으나, List의 pop 메소드로 스택의 모든 연산을 수행할 수 있습니다.
def iterative_dfs(start):
visited = [] # 방문한 정점
stack = [start] # 시작 정점부터 시작
while stack:
v = stack.pop() # 방문할 정점을 스택에서 가져오기
if v not in visited: # 해당 정점을 방문하지 않았다면
visited.append(v) # 해당 정점 방문
stack += graph[v] - set(visited)
# 해당 정점과 인접한 정점 중 방문하지 않은 정점을 스택에 추가
return visited # 방문한 결과 반환2) 재귀호출을 이용하여 구현
def recursive_dfs(start, visited = None):
if visited is None:
visited = []
visited.append(start) # 시작 정점부터 시작
for w in graph[start]: # 시작 정점과 인접한 노드를 순회
if w not in visited: # 인접한 노드을 방문하지 않았다면
visited = recursive_dfs(w, visited)
# 해당 노드를 시작 노드로 삼아 재귀적으로 DFS 시작
return visited # 방문한 결과 반환2. 너비 우선 탐색(BFS, Breath First Search)
- 시작 정점(일반적으로 루트 정점)에서 시작하여, 인접한 정점를 먼저 탐색하는 방법
- 주로 큐로 구현하며, 그래프의 최단 경로를 구하는 문제에 주로 사용합니다.
1) 스택을 이용하여 구현
- 파이썬의 List를 Stack으로도 사용할 수 있지만, pop 메소드를 사용하여 Queue로도 사용할 수 있으나 큐의 front에서 데이터를 가져오기 위해 쓰이는 pop(0) 메소드의 시간복잡도가 O(n)이므로 효율이 좋지 못하다.
- 따라서 Queue 자료구조의 경우는 collections의 deque를 사용하는 것이 좋다.
def iterative_bfs(start):
visited = [] # 방문한 정점
queue = collections.deque([start]) # 시작 정점부터 시작
while queue:
v = queue.popleft() # 방문할 정점 큐에서 가져오기
if v not in visited: # 해당 정점을 방문하지 않았다면
visited.append(v) # 해당 정점 방문
queue += graph[v] - set(visited)
# 해당 정점과 인접한 정점 중 방문하지 않은 정점을 스택에 추가
return visited # 방문한 결과 반환2) 재귀호출을 이용하여 구현
- 재귀호출로 구현이 불가능하다. 이를 명심하고 있어야한다.
백트래킹
해결책에 대한 후보를 구축해 나아가다 가능성이 없다고 판단되는 즉시 후보를 포기하고 왔던 길을 되돌아가 정답을 찾아가는 범용적인 알고리즘으로 제약 충족 문제에 특히 유용
- DFS는 백트래킹의 골격을 이루는 알고리즘이며, 백트래킹은 주로 재귀로 구현한다.
- 브루트 포스와 유사하다고 볼 수 있지만 한번 방문 후 가능성이 없는 경우에는 즉시 그만 둔다는 점에서 차이가 있다.
용어
- 가지치기 : 트리를 탐색하여 가능성이 없는 가지를 포기하는 작업이며 트리의 탐색 최적화 문제와 관련이 깊다.
- 제약 충족 문제 : 수많은 제약 조건을 충족하는 상태를 찾아내는 수학 문제