interpolation ~ 보간법이란?

이미지를 기하학적 변환하는 방법 중 하나가 interpolation(보간)이다.

수치해석학의 수학 분야에서 보간법이란 알려진 데이터 지점의 고립점 내에서 새로운 데이터 지점을 구성하는 방식을 의미한다.

대표적으로 선형 보간법, 이중 선형 보간법, 포물선 보간법 등이 있다.
구글에 보간법을 검색하면 수학적으로 아주 잘 알려준다. 👍
하지만 오늘 내가 공부해볼 것은 이미지처리에서의 보간법이다.

정의

image interpolation은 지털 이미지의 해상도를 변경하거나 크기를 조정할 때 사용되는 기법이다. 새로운 픽셀 값을 계산하여 원래 이미지의 픽셀들 사이에 새로운 픽셀을 삽입함으로써 이미지를 확장하거나 축소할 수 있다.

종류

주요 이미지 보간법은 4가지로 정리할 수 있다.

• Nearest Neighbor Interpolation (최근접 이웃 보간법)
• Bilinear Interpolation (양선형 보간법)
• Bicubic Interpolation (양입방 보간법)
• Higher-Order Interpolation (고차원 보간법)

다음과 같은 2X2 이미지를 5X5로 확대한다는 가정하에 설명을 해보겠습니당.

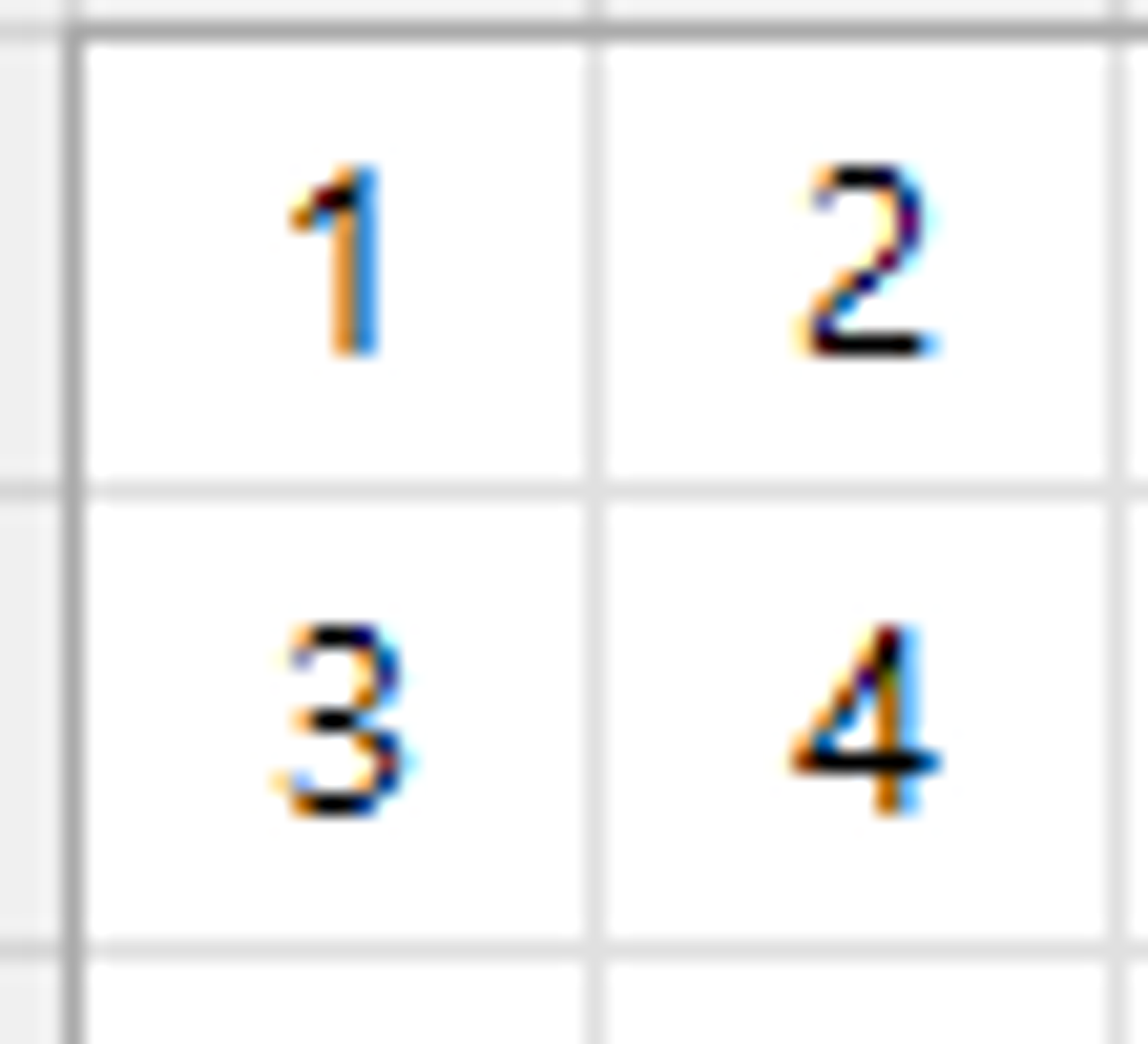
Nearest Neighbor Interpolation

가장 간단한 방법으로, 새로운 픽셀의 값을 주변의 가장 가까운 원본 픽셀의 값으로 설정한다.
장점 : 계산이 빠르고 구현이 간단하다.
단점 : 이미지의 경계가 거칠고 aliasing이 나타날 수 있다.

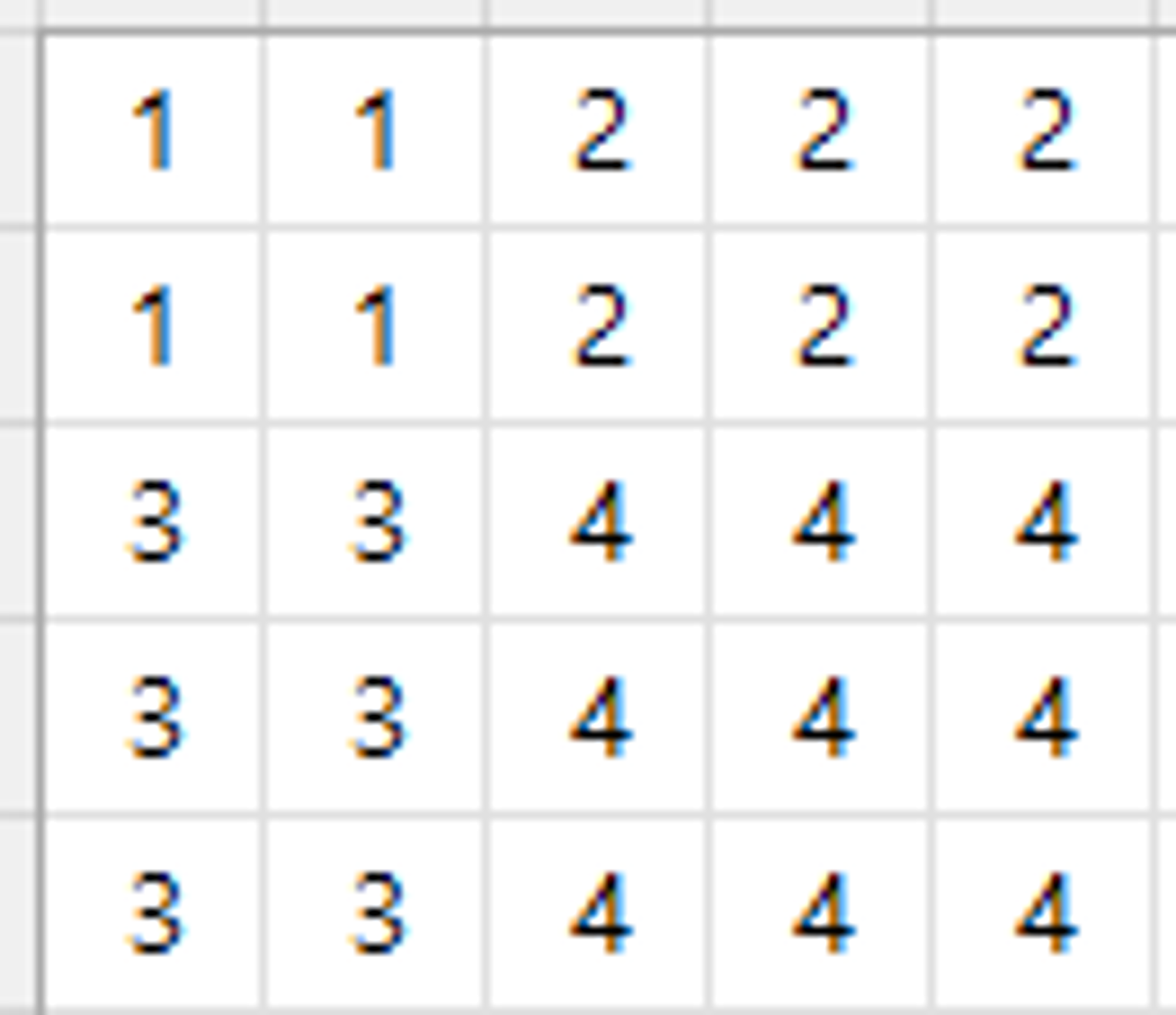
이미지만 봐도 이해가 바로 될 것이라고 생각한다.
크기가 늘어나는 정도를 고려하여 기존 값으로 빈값을 채운다.

Bilinear Interpolation

linear interpolation을 2차원으로 확장시킨 보간법이다. 새로운 픽셀의 값을 원본 이미지의 4개의 인접 픽셀 값을 사용하여 선형적으로 계산한다.
장점 : 가장 가까운 이웃 보간법보다 부드러운 결과를 제공한다.
단점 : 계산량이 약간 증가한다.

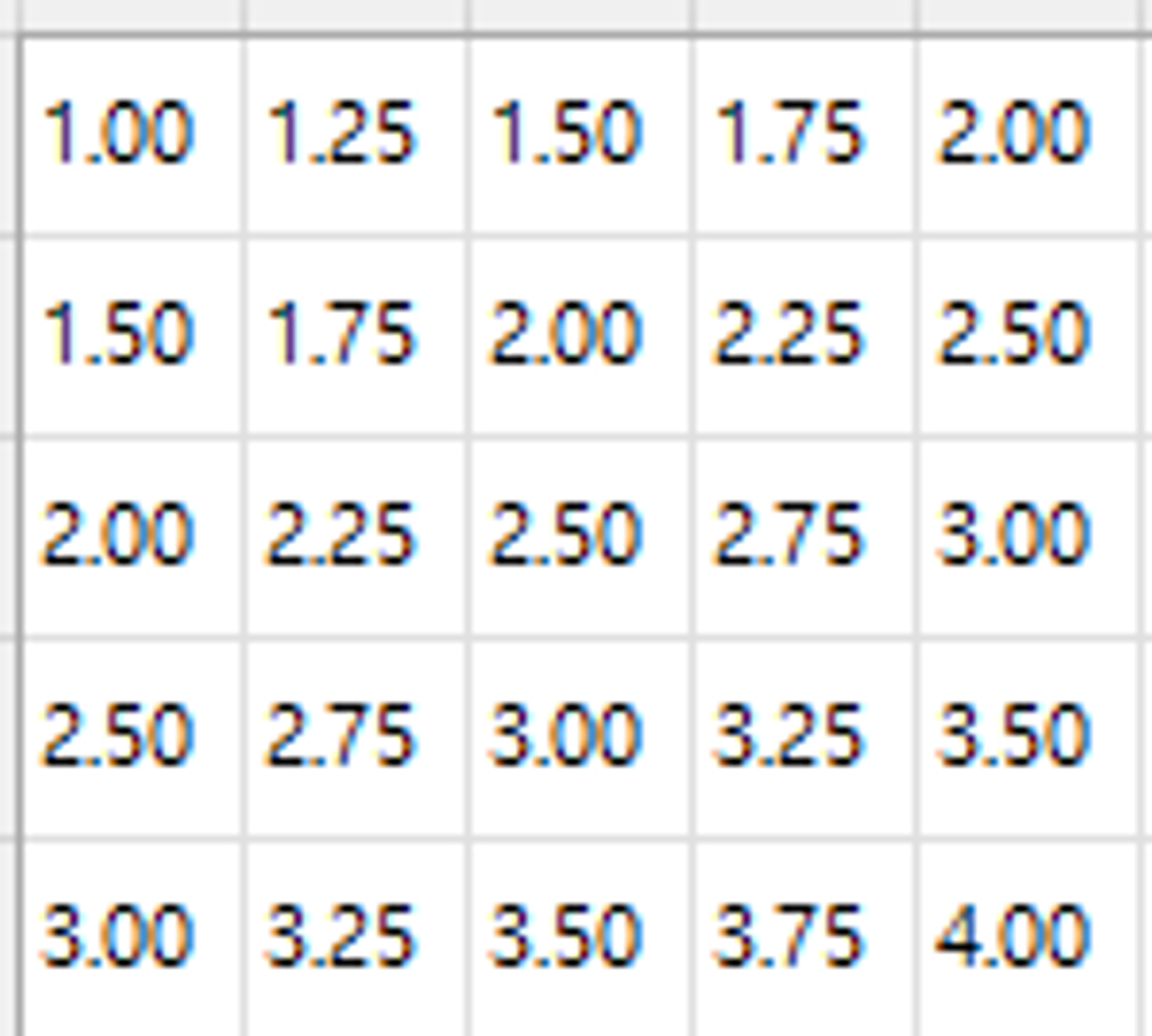
이제부터는 조금 복잡해진다. (조금.. 아니 어쩌면 많이)
Bilinear Interpolation에서 새로운 픽셀 값을 계산하는 공식은 다음과 같다.

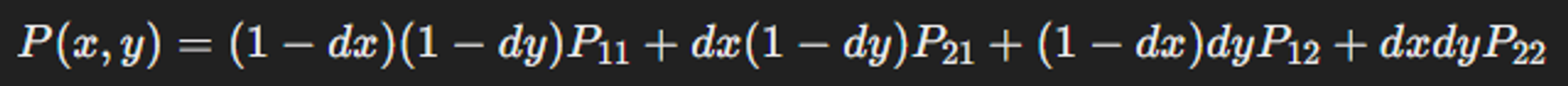
이 분 블로그를 참고하면 더 이해하기 쉽다.

결과적으로는 네 개의 인접한 점들의 값과 그에 따른 면적을 가중치로 하여 구하게 된다.

혹시 그래도 이해가 안간 분들을 위해서 설명을 덧붙여보자면..
Bilinear은 반대 면적의 가중치를 곱해주는 방식인건데,
A좌표에는 a넓이(dxdy)를, B좌표에는 b넓이((1-dx)dy)를 곱해줘야하는 것이다.
(볼펜 색이 2가지 밖에 없어서 피치 못하게 2개밖에 표현을 못했다.)

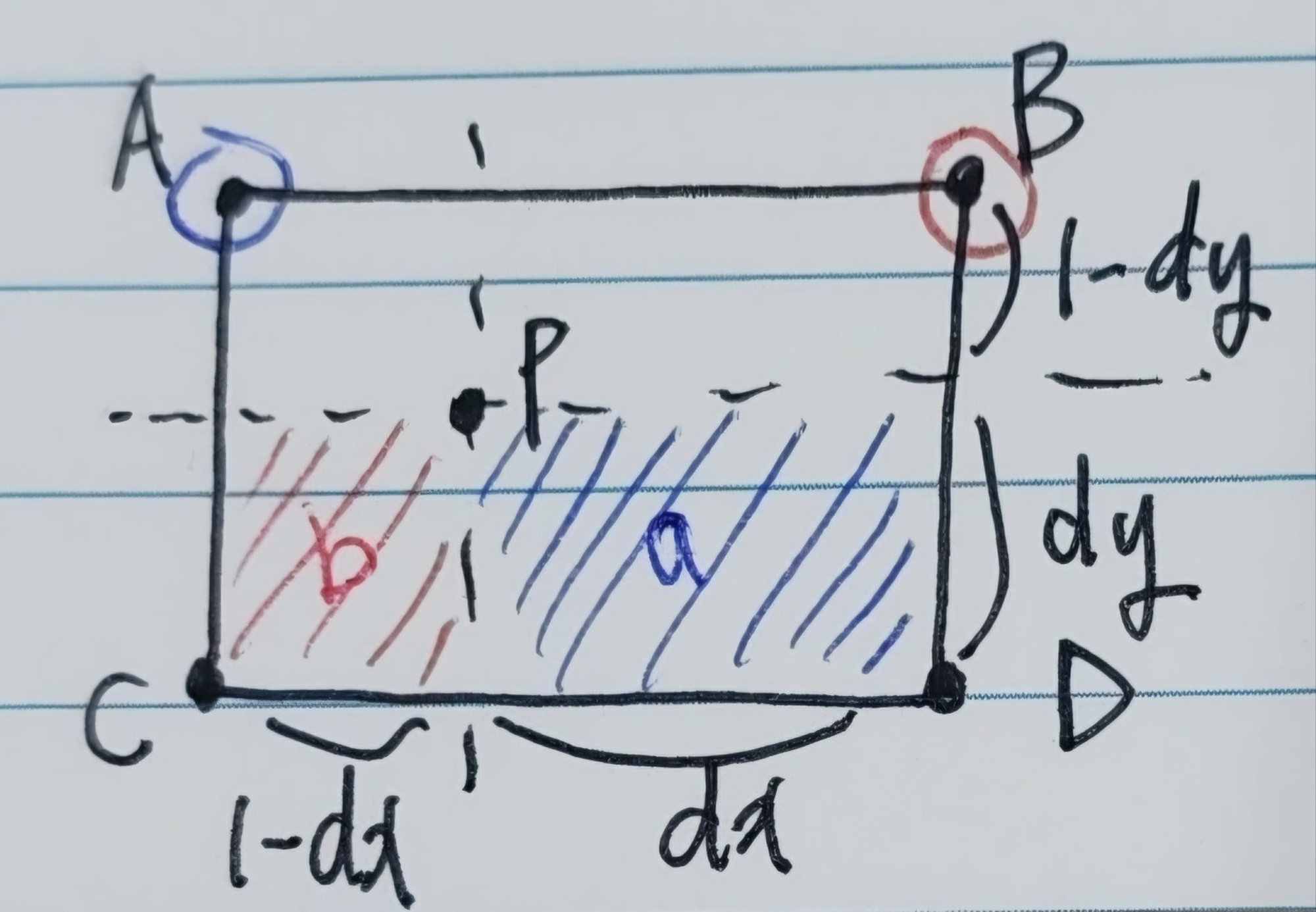
이걸 우리가 구하려는 변환에 적용해보자면 아래 사진과 같다. 쉽게 말하면 비율을 가중치로 곱해주면 된다 ! (복잡 생각 노노)

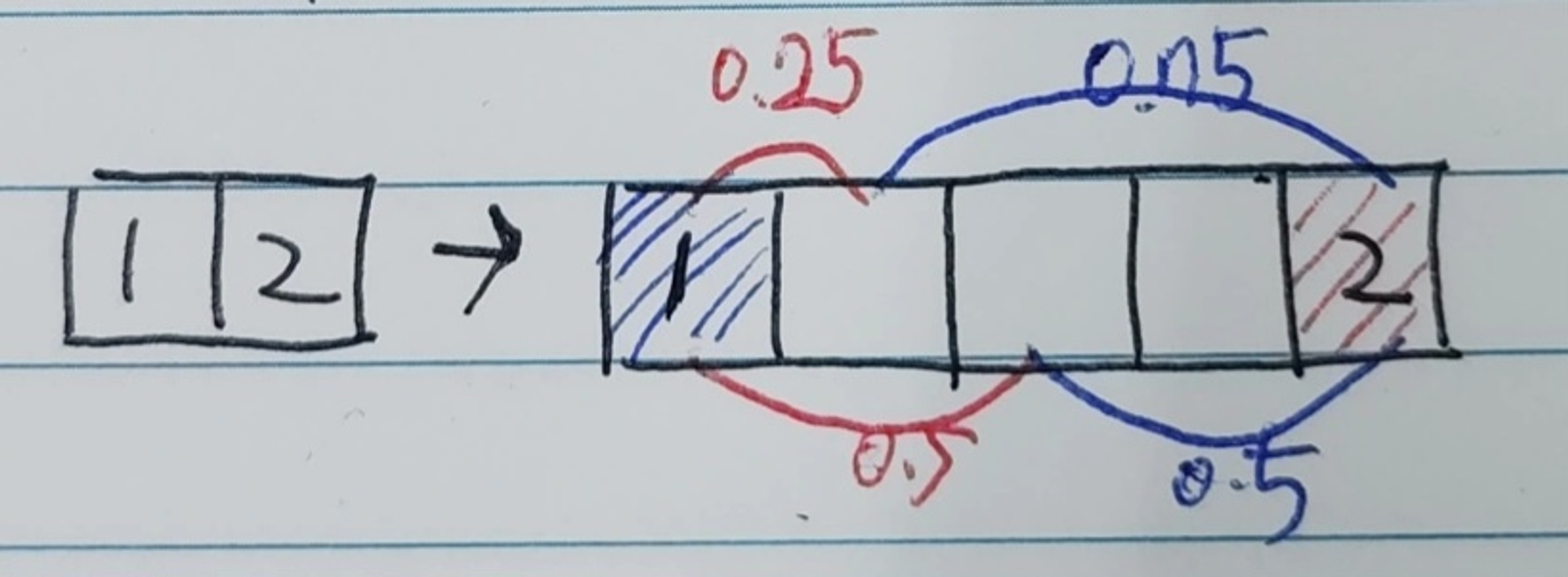
Bicubic Interpolation

새로운 픽셀의 값을 원본 이미지의 16개의 인접 픽셀 값을 사용하여 계산한다. 3차 함수(큐빅 함수)를 사용하여 보간한다.
장점: 양선형 보간법보다 더 부드러운 결과를 제공한다.
단점: 계산량이 많이 증가한다.

솔직히 말하며 내 뇌로 이해하기 어려운 정도까지 왔다.
cubic interpolation(삼차 보간법)을 2차원으로 확장시킨 것이 bicubic interpolation이다.
이 블로그에서 친절하게 설명해주니 이해하고 싶다면 이 블로그를 참조하는 것이 좋을 것같다 👍

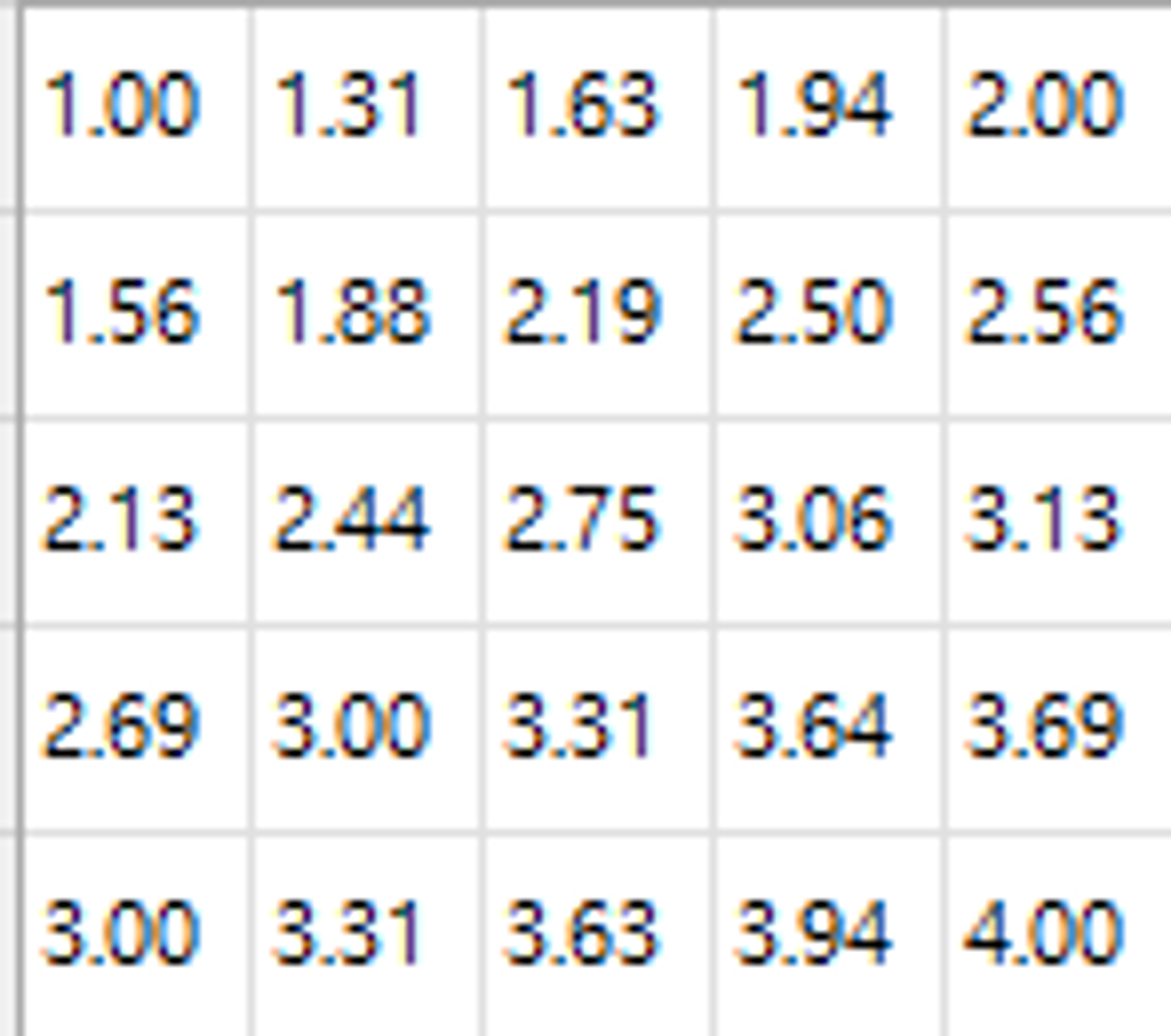
삼차 보간법은 4개의 이웃점을 필요로 한다. 삼차보간법을 2차원으로 확장시킨 것이 쌍삼차 보간법이다. 즉, 16(=4X4)개의 점을 참조한다.

Bicubic interpolation에서 새로운 픽셀 값을 계산하는 공식은 다음과 같다.

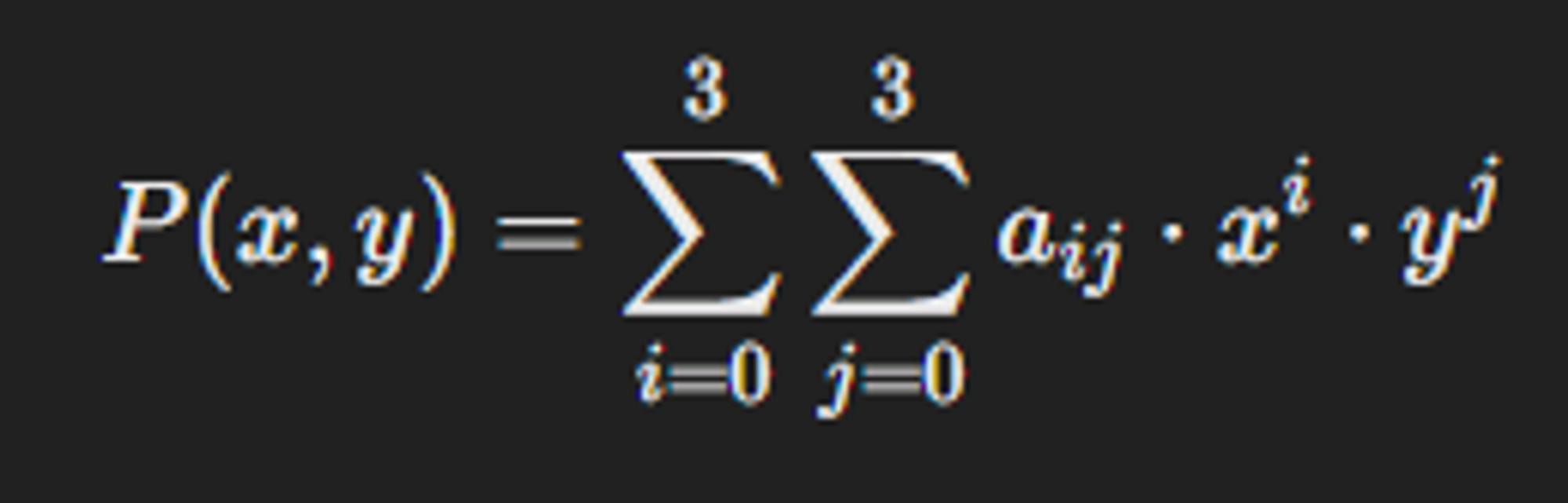
여기서 aij는 보간할 픽셀 주변의 16개의 픽셀에서 계산된 계수 값이다.
여기서.. aij 계산하는게 전혀.. 무슨 말인지 모르겠어서 일단은 스킵하고.. 혹시나 이해할 계기가 생긴다면 돌아와서 설명을 다시 적어보겠다. (영원히 다시 안돌아올듯 ㅜ) 아무튼간에 주변 16개를 참고하여 계산한다는 것을 알아두면 된다!

Higher-Order Interpolation

1차원 데이터를 2차원, 3차원 등 고차원 데이터로 변환하여 보간한다. 대표적으로 Lanczos Interpolation이 있다.
여기서 수학적인 설명은 더 이상 생략하겠다. (… 디지털 신호처리 책 읽고 나오면 진짜 제가 설명해드릴게요.. 나 이제 지쳤어.. 흑흑)

실습

하지만 뭐다? 우리에게는 이런 복잡한 원리들은 아 그렇구나 ~ (그렇구나도 안되긴 함.. 사실 ㅜ) 하고 넘어가면 된다.
왜냐면 머찐 사람들이 이미 다 api를 만들어두었답니다?
나의 절친(아님) opencv에서 resize 시 이러한 것들을 모두 제공해주고 있다 👍
resize 시 interpolation flag들은 여기서 확인 가능하다 ~

아래 코드는 위의 사진처럼 모카를 더 큰 사이즈로 볼 수 있게 바꾸는 코드이다.

#include <opencv2/opencv.hpp>
#include <iostream>

using namespace cv;
using namespace std;

int main() {
	string file = "mocha.png";
	Mat src = imread(file, IMREAD_COLOR);

	if (src.empty()) {
	cout << "Image load failed!" << endl;
	return -1;
	}

	int col = src.cols*4;
	int row = src.rows*4;

	cout << col << endl << row << endl;

	Mat origin;
	resize(src, origin, Size(col, row));
	Mat nearest;
	resize(src, nearest, Size(col, row), INTER_NEAREST);
	Mat linear;
	resize(src, linear, Size(col, row), INTER_LINEAR);
	Mat cubic;
	resize(src, cubic, Size(col, row), INTER_CUBIC);
	Mat lanczo;
	resize(src, lanczo, Size(col, row), INTER_LANCZOS4);

	namedWindow("src", WINDOW_AUTOSIZE);
	namedWindow("origin", WINDOW_AUTOSIZE);
	namedWindow("nearest", WINDOW_AUTOSIZE);
	namedWindow("linear", WINDOW_AUTOSIZE);
	namedWindow("cubic", WINDOW_AUTOSIZE);
	namedWindow("lanczo", WINDOW_AUTOSIZE);

	imshow("src", src);
	imshow("origin", origin(Rect(0, 0, 350, 350)));
	imshow("nearest", nearest(Rect(0, 0, 350, 350)));
	imshow("linear", linear(Rect(0, 0, 350, 350)));
	imshow("cubic", cubic(Rect(0, 0, 350, 350)));
	imshow("lanczo", lanczo(Rect(0, 0, 350, 350)));

	waitKey(0);

	return 0;
}

결과는 다음과 같다...

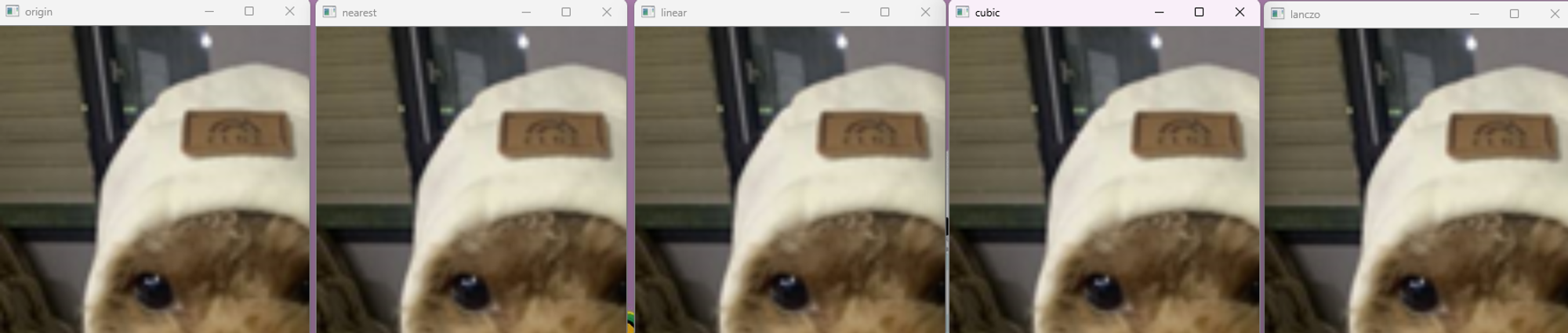
위 사진이 4배 한 사진이고 아래는 6, 8배 .. 10배까지도 해서 비교해본 사진이다.
보다시피 알겠지만 뭐.. 이것들 사이에 어떤 차이가 있긴하나..? 싶다.
이래서 모든 opencv에는 예시 사진이 존재하는구나 싶었음 ㅋㅋ
원본 이미지 품질이 좋아서 그런지 확대를 엄청해도 큰 차이가 보이지 않는다..
제대로된 결과를 보고싶다면 이 분 블로그를 대신 참고해주세옴... 나중에 시간되면 제대로 된 예시를 글에 추가해보겠습니다. (절대 안함)

---

그럼 보간법에 관한 글을 여기까지 쓰는걸로 ~ (끄적끄적 ✏️)