이 기법은 메모리 측면에서 효율적으로 사용하기 위한 알고리즘입니다

위 사진에서 Qn, Qn+1 과 같이 보기에 복잡한 영어 수식들이 존재하는데요
쉽게 말하자면 Qn은 n-1개의 숫자가 존재할때 그에 대한 평균을 구하는 수식이며
Qn+1은 n개의 숫자에 대해 평균을 구하는 수식입니다
하지만 두가지는 계산 방식에서 차이가 납니다
일반식
왼쪽 수식은 매번 숫자가 늘어날때마다 이전의 모든 숫자들을 다 더해줘야 합니다
예를 들어 4개의 숫자에 대한 평균을 구하여 Q5에 대한 결과를 계산했다고 가정해봅시다
이후 다시 추가 계산이 필요하여 1개의 숫자가 늘어나 Q6에 대한 계산을 한다면
다시 처음부터 R1 + R2 + R3 ... + R(n-1) 까지 더한 뒤 그 개수로 나눠줘야 합니다
이 더하는 과정에서 메모리 낭비가 매우 심해집니다
이미 이전에 계산한 평균(Q5) 에 대한 결과값을 다시 재 사용할 수 없을까? 에 대한 것이 오른쪽에 나와있는 Qn+1 에 대한 식입니다
Incremental Implementation
오른쪽에 나와있는 식들은 n개의 숫자에 대한 평균을 구하는 식이며
결국 가장 위의 식을 Qn(이전에 계산한 평균 결과값) 을 사용하기 위해 정리한 내용들 입니다
천천히 식을 따라가 보겠습니다
Qn+1 은 숫자들을 n개 더한 뒤 n으로 나눠줍니다
이 시그마 Ri 부분은 다시 n-1 까지의 숫자들을 더한 값과 Rn 으로 나눌 수 있습니다
여기서 다시 n-1 부분을 평균값으로 식을 풀어내어 (n-1)Qn 식을 얻을 수 있습니다
이 내용을 다시 보기 쉽게 정리하면 가장 아래식인
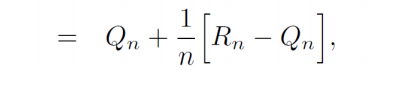
가 나오게 됩니다
이 식에서 Qn 이 존재하므로 이를 사용하여 메모리 사용에 대한 효율을 증가시키는 것이 목적입니다
새로운 값이 들어올때 마다
- 이전에 계산했던 평균 값을 사용하므로 그만큼의 메모리 효율이 올라가게 되며
- 메모리 공간이 늘어나지 않아도 되는
장점이 있습니다
