알고리즘 - 구간 합

이번 글에서는 구간합에 대해 알아보도록 하겠습니다

구간합이란 합 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘입니다. 사용빈도가 높으니 잘 이해하고 넘어가도록 합시다

구간합의 핵심 이론

인덱스 0부터 각 인덱스 위치까지의 합배열을 구한 뒤 만약 a 부터 b 까지의 구간합을 구하고 싶다면 b합배열 - a 합배열 을 해주는 방식으로 구하는 원리입니다

이렇게 합 배열을 미리 구해놓은 뒤 연산을 통해 구간합을 구하게 되면 시간 복잡도가 O(N)에서 O(1)로 감소합니다

구간 합 알고리즘을 활용하려면 먼저 합 배열을 구해야 합니다. 배열 A가 있을 때 전체 합 배열 S는 다음과 같이 정의합니다

S[i] = S[i-1] + A[i]

구간합 역시 쉽게 구할 수 있습니다. i에서 j까지 구간합을 구하는 공식은 다음과 같습니다

S[j] - S[i-1]

백준 11659 구간 합

구간합은 합 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘입니다

문제 분석

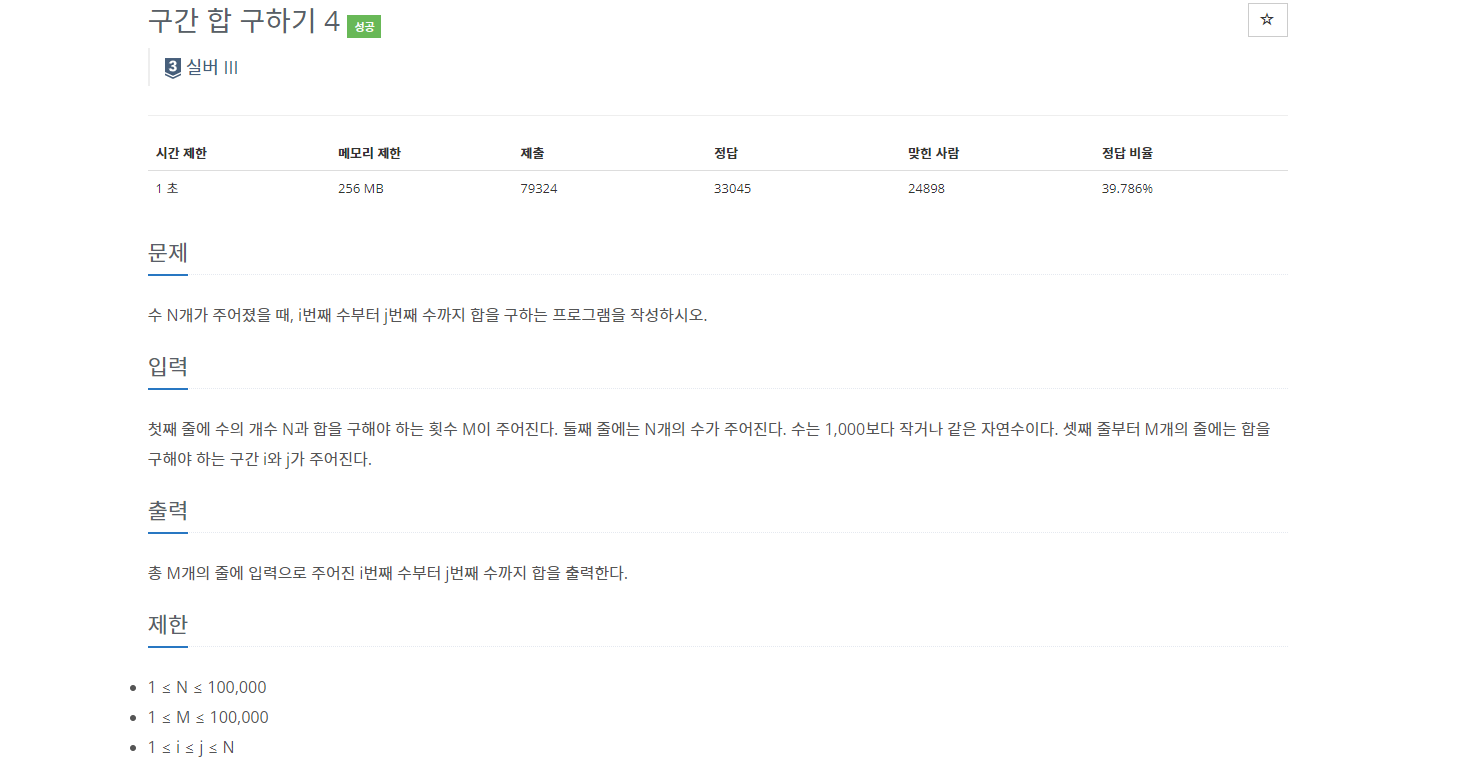
N 개의 수가 주어졌을때 일정 범위 내에 있는 구간의 합을 구하라는 문제입니다

입력은 최대 100,000 이며 합을 구하는 반복횟수도 최대 100,000 입니다

시간복잡도

만약 구간합을 조건이 주어질때마다 매번 덧셈 연산을 순차적으로 진행하며 구하게 되면

최악의 경우 100,000번의 숫자들을 합하는 연산은 최대 100,000 번이므로 이는 100,000 * 100,000 = 10,000,000,000 즉 10억 번이라는 너무 큰 연산횟수가 발생됩니다

1억번의 연산횟수를 약 1초라고 가정하면 10초가 발생됩니다

시간 제한은 1초 이므로 위 알고리즘을 사용하여 제출하게 된다면 시간초과가 발생할 수 있습니다

그러므로 구간 합 알고리즘을 떠올려볼 수 있습니다

미리 합배열을 생성할때는 최악의 경우 100,000 번의 숫자들에 대해 합배열을 생성할 당시의 시간 복잡도인 O(N)이 발생하게 되며 구간합 연산시 각 인덱스 사이의 빼기 연산을 1번만 하면 되므로 O(1)이 발생하여 100,000 번의 숫자들을 합하는 연산인 100,000 번 즉 10만번의 연산횟수가 발생하므로 약 0.001초의 시간복잡도가 발생합니다

슈도코드

for (숫자 개수만큼 반복하기) {
	합 배열 생성 S[i] = s[i-1] + A[i]
}

for (질의 개수만큼 반복하기) {
	질의 범위 받기(i~j)
    구간 합 출력하기(S[j] - S[i-1])
}

정답코드

package org.example;

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) {
        BufferedReader br = null;

        try {
            br = new BufferedReader(new InputStreamReader(System.in));

            StringTokenizer st1 = new StringTokenizer(br.readLine());
            StringTokenizer st2 = new StringTokenizer(br.readLine());

            int N = Integer.parseInt(st1.nextToken());
            int M = Integer.parseInt(st1.nextToken());

            long[] S = new long[N + 1];

            for (int i = 1; i < N + 1; i++) {
                S[i] = S[i - 1] + Integer.parseInt(st2.nextToken());
            }

            for (int i = 0; i < M; i++) {
                StringTokenizer st = new StringTokenizer(br.readLine());
                int I = Integer.parseInt(st.nextToken());
                int J = Integer.valueOf(st.nextToken());

                System.out.println(S[J] - S[I - 1]);
            }
        } catch (Exception e) {
            e.getStackTrace();
        } finally {
            try {
                br.close();
            } catch (Exception e) {
            }
        }
    }
}