백준 1978 소수찾기, 4948번 베르트랑 공준

Jake·2022년 10월 16일

백준 알고리즘

알고리즘

목록 보기

1/16

소수

베르트랑 공준 문제를 풀기 위해 여러 알고리즘들을 찾아보았는데 소수를 찾을때 이 알고리즘을 사용하면 매우매우 효율이 좋아지는걸 알게되었다.

그리고 개인적으로 소수가 실생활에서 사용되는 예시들은 어떤게 있을까 궁금하여 찾아봤더니

금융 세계와 정보 시스템에서 기본적으로 사용되는 암호 및 비밀 키 생성.

소수를 생의 주기로 삼으면 천적을 피하기 쉽다

예라고 하기엔 좀 뭐하지만 유명한 스포츠선수 들의 백넘버는 주로 13, 7, 17.. 등등 유명 운동선수들이 소수를 즐겨 하는 이유는 더 이상 나누어 지지 않는 수 라서..? (박지성, 손흥민, 덕배 등등..)

등이 있다고 한다.

소수찾기 자체의 알고리즘은 비교적 쉽다

소수의 정의를 알고싶으신 분은 위키백과를 참고해보자

소수란?
1보다 큰 자연수 중 1과 자기 자신만을 약수로 가지는 수

소수를 알아보자

2, 3, 5, 7, 11, 13, 17 …

소수는 위와 같이 약수가 1과 자기자신밖에 없다.

그럼 n 이 주어졌을때 n이 소수인지 아닌지는 어떻게 판단할까 ?

소수의 정의를 이용해보면 된다.

2부터 n까지의 수를 이용하여 n을 나누어 보았을때 1번이라도 나누어 떨어지면 그 수는 1을 제외한 약수를 가지므로 소수가 아니다.

이를 코드로 아래와 같이 나타낼 수 있다.

for (int i = 2; i < num; i++) {
            if (num % i == 0) return false;
        }

이렇게 하면 문제는 해결되지만 시간복잡도가 매우 크다

시간복잡도란?

시간 복잡도는 어떤 알고리즘의 성능 측정 지표 중 하나로, 얼마나 빠르게 연산이 가능한지를 측정하는 지표이다. 시간복잡도 내에서도 Big-O, Big-Omega, Big-Theta 세 종류가 있지만 보통 Big-O표기법이 가장 많이 쓰인다.

Big-O 표기법은 O형식으로 표기하며 뜻은 최악의 경우 최고차항 만큼의 연산을 해야한다는 것이다.

예를들어 구구단의 경우 1부터 n 까지 n 단을 구하는 코드의 시간 복잡도를 Big-O로 표기하면 어떻게 될까?

답은 O(n^2) 가 된다.

왜냐하면 n가지 경우의 수가 n개 존재하기에 n^2가 모든 경우의 수가 된다.

아래 코드를 보자

public static void gugudan(int n) {
        for (int i = 1; i < n+1; i++) {
            for (int j = 1; j < 10; j++) {
                System.out.printf("%d * %d = %d\n", i, j, i*j);
            }
        }
    }

위와 같은 논리로 1개의 수가 소수인지 아닌지를 판단하기 위해서는 n번의 연산이 필요하므로 시간 복잡도가 O(n)이 되는 것이고 만약 n개의 수를 소수인지 아닌지 판단하기 위해서는 n*n번이 필요하므로 시간 복잡도가 O(n^2)가 되는 것이다.

시간 복잡도에서 O(n^2)의 시간 복잡도를 갖는다는 것은 가장 느린 시간 알고리즘을 의미한다.

처음 우리가 소수를 구하기 위해 2부터 n까지를 모두 나누며 소수를 판단하였다.

그럼 이 방법이 최선인가를 고민해보았을때 그것은 아니라는 것이다.

결론을 말하자면 우린 n까지를 나누는 것이 아니라 n의 제곱근까지만 나누어 보아도 그 수가 소수인지 아닌지를 판단할 수 있다.

제곱근을 사용할 수 있는 이유

왜 우리는 n이 소수인지 아닌지를 판단하기 위해 n까지가 아닌 n의 제곱근까지만 나누어 보아도 되는 것일까 ?

예를들어 24의 약수를 구한다고 가정해보자.

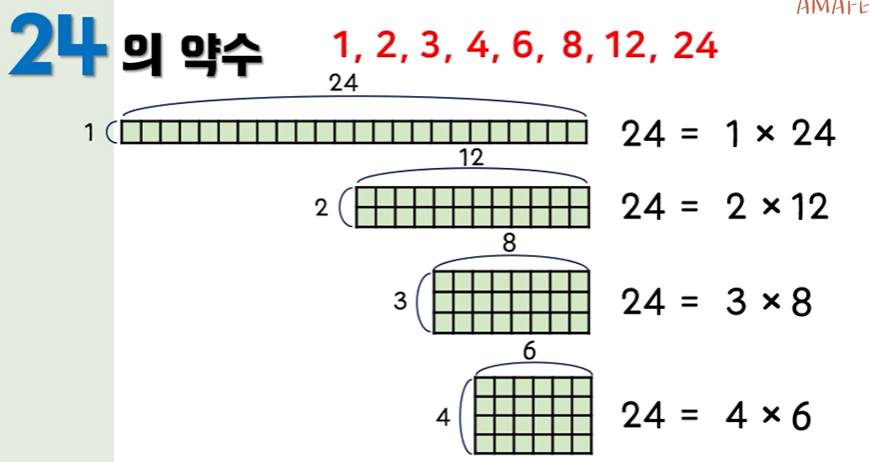
24의 약수 8개를 찾아보았다.

1부터 시작하여 차례대로 구해보았다.

하지만 위 과정에서 우리가 총 8 번의 연산을 하였을까 ? -> 아니다.

1, 2, 3, 4, 로는 나누어 보았지만 6, 8, 12, 24로는 나누어 보지 않았다.

이는 1, 2, 3, 4로 나눌때 그 몫이 각각 6, 8, 12, 24였기 때문이다.

세로의 길이에 따라 가로의 길이가 정해지는 것처럼 약수는 한 쌍씩 짝을 지어 찾을 수 있다.

여기서 핵심을 찾을 수 있다.

우리는 24를 소수판단할때 4까지만 나누어 보아도 된다는 의미이다.

우리가 24라는 수를 두개의 수로 곱하여 구하려면 a*b = 24형태로 나타낼 수 있다. 여기서 a와 b 중 하나는 무조건 24의 제곱근보다 같거나 크다.

(이는 잘 생각해보면 금방 그 이유를 알 수 있다.)

그러면 왜 4까지만 나눠보아도 되는걸까 ?

왜냐하면 제곱근을 넘어가는 순간 반복이 되기 때문이다.

위에서 24의 약수는 1, 2, 3, 4, 6, 8, 12, 24 라고 구하였다.

여기서 4를 넘어가는 순간 [6 * 4], [8 * 3], [24 * 1] 과 같이 처음 연산했던 것과 같은 연산을 반복하기 때문에 이미 이전에 찾았기 때문이다.

이는 우리가 제곱근까지 나누어보아도 된다는 의미를 나타낸다.

107이 소수인지 아닌지를 판단해보자

그럼 몇번째 수 까지 판단하면 될까 ?

그렇다 107의 제곱근보다 같거나 작은 자연수인 10이다.

하지만 10은 소수가 아니니 10보다 작은 소수는 7이다.

즉 2, 3, 5, 7 까지만 107과 나누어 보고 나누어지지 않는다면 107은 소수라는 것이다.

베르트랑 공준

문제 n이 주어졌을때 n 부터 2n까지의 소수를 구해라

소스코드는 아래와 같다.

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (true) {
            int n = sc.nextInt();
            if (n == 0) {
                break;
            }
            int cnt = 0;

            for(int i=n+1; i<=2*n; i++) {
                if(isPrime(i)) {
                    cnt ++;
                }
            }System.out.println(cnt);

        }
    }

    public static boolean isPrime(int Number) {
        if(Number == 1) {
            return false;
        }

        for (int i=2; i<=Math.sqrt(Number); i++) {
            if(Number%i == 0) return false;
        }
        return true;
    }
}