알고리즘 - BFS 너비 우선 탐색

Jake·2023년 7월 14일

알고리즘

목록 보기

16/16

너비 우선 탐색은 그래프를 완전 탐색하는 방법 중 하나로, 시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘이다

아래 사진을 통해 쉽게 이해해보겠습니다

DFS(깊이 우선 탐색) vs BFS(너비 우선 탐색)

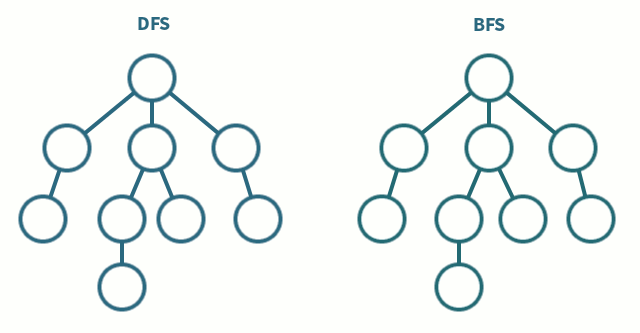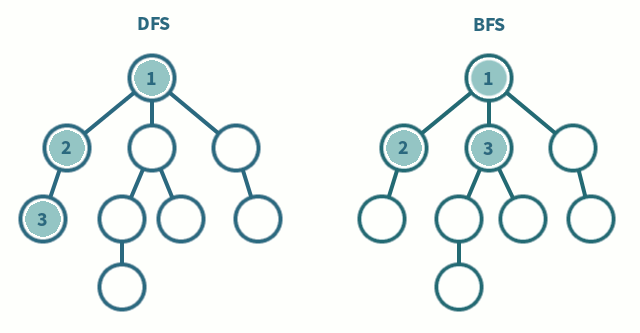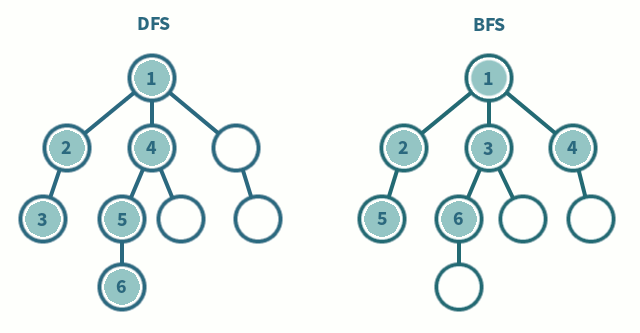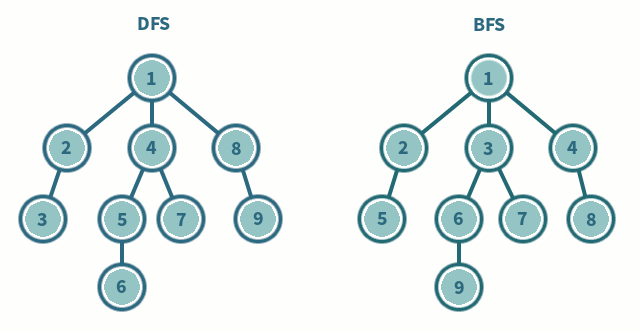
사진출처 - DFS

핵심이론

BFS도 DFS와 마찬가지로 한 번 방문한 노드는 다시 방문하면 안되므로 방문 여부를 체크할 배열이 필요하며, 그래프는 인접행렬, 인접 리스트 2가지 중 하나로 표현할 수 있습니다

BFS의 탐색 방식은 선입 선출 FIFO 특성을 가지므로 큐를 사용해서 설명합니다

너비 우선 탐색은 아래 순서로 진행되며 2번이 핵심이론입니다

BFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
큐에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 큐에 삽입하기
큐 자료구조에 값이 없을 때까지 반복하기

2번에서 꺼낸 노드의 인접한 노드를 다시 큐에 삽입할때 해당 노드가 이전에 탐색을 완료하였는지 여부를 체크하며 방문을 하였다면 큐에 삽입하지 않고 다음 인접노드를 탐색합니다

즉, BFS는 한 루트에서 해당 노드에 연결된 모든 노드들을 먼저 탐색하고, 그 다음, 다음 깊이로 넘어가서 탐색하는 형태입니다

최단 경로를 알 수 있는 특징이 있습니다

여기서 최단 경로란, 시작 노드에서 목표 노드까지 가는데 필요한 최소한의 간선 수를 의미합니다. BFS는 탐색을 넓게 진행하면서 시작 노드로부터 점차 멀어지는 순서로 노드를 탐색하기 때문에, 시작 노드와의 거리가 가까운 순서로 노드를 발견하게 됩니다.

BFS는 큐를 사용하여 탐색을 진행하기 때문에, 시작 노드에서 각 노드까지의 최단 경로를 계산할 수 있습니다. 탐색 과정에서 각 노드를 방문할 때, 해당 노드에 도달하는 최단 경로가 이미 계산되어 큐에 저장되어 있습니다. 따라서 BFS를 사용하여 모든 노드를 탐색하면서 최단 경로를 계산하게 됩니다.

BFS 알고리즘을 통한 최단 경로 계산 예시는 아래와 같습니다

		  A
        /   \
       B     C
      / \   / \
     D   E F   G

시작 노드 A에서 BFS 탐색을 시작합니다. 큐에는 처음에 시작 노드 A가 들어갑니다. 그리고 BFS 탐색이 진행되면서 큐의 상태와 방문한 노드 순서가 업데이트됩니다

아래는 시간 순서대로 쉽게 예시를 들어보았습니다

BFS 탐색 시작: 큐에 A가 들어가고, A를 방문했습니다.
```
lessCopy code
큐: A
방문한 노드: A
```
A를 큐에서 꺼내고 인접한 노드 B와 C를 큐에 넣습니다. B와 C를 방문했습니다.
```
lessCopy code
큐: B, C
방문한 노드: A, B, C
```
B를 큐에서 꺼내고 인접한 노드 D와 E를 큐에 넣습니다. D와 E를 방문했습니다.
```
mathematicaCopy code
큐: C, D, E
방문한 노드: A, B, C, D, E
```
C를 큐에서 꺼내고 인접한 노드 F와 G를 큐에 넣습니다. F와 G를 방문했습니다.
```
mathematicaCopy code
큐: D, E, F, G
방문한 노드: A, B, C, D, E, F, G
```
D를 큐에서 꺼냅니다. D의 인접한 노드가 없으므로 넘어갑니다.
```
mathematicaCopy code
큐: E, F, G
방문한 노드: A, B, C, D, E, F, G
```
E를 큐에서 꺼냅니다. E의 인접한 노드가 없으므로 넘어갑니다.
```
mathematicaCopy code
큐: F, G
방문한 노드: A, B, C, D, E, F, G
```
F를 큐에서 꺼냅니다. F의 인접한 노드가 없으므로 넘어갑니다.
```
mathematicaCopy code
큐: G
방문한 노드: A, B, C, D, E, F, G
```
G를 큐에서 꺼냅니다. G의 인접한 노드가 없으므로 넘어갑니다.
```
mathematicaCopy code
큐: -
방문한 노드: A, B, C, D, E, F, G
```

위와 같이 BFS 탐색을 진행하면서 큐의 상태와 방문한 노드 순서가 업데이트됩니다. BFS는 큐를 사용하여 시작 노드로부터 가까운 순서대로 노드를 방문하기 때문에, 방문한 노드 순서는 최단 경로를 나타냅니다

최단 경로 결과

A에서 A까지의 최단 경로: [A]
A에서 B까지의 최단 경로: [A, B]
A에서 C까지의 최단 경로: [A, C]
A에서 D까지의 최단 경로: [A, B, D]
A에서 E까지의 최단 경로: [A, B, E]
A에서 F까지의 최단 경로: [A, C, F]
A에서 G까지의 최단 경로: [A, C, G]

시간복잡도

O(N^2)

최악의 경우 N^2의 복잡도입니다

가지치기를 이용해서 잘라내기를 하면(백트래킹), 해당 노드의 자식이 모두 잘라지는 효과 있음 (복잡도를 줄일 수 있음)
그래프의 표현을 인접 행렬 O(V^2) 대신, 인접 리스트 사용시 O(V + E)로 줄일 수 있습니다V: 정점(Vector), E: 간선(Edge)

구현

필요 요소 3가지

그래프를 표현한 자료구조 ArrauList, Array[][]
방문 정보를 기록하기 위한 테이블 int visited[]
출발 노드와, 출발 노드에서 갈 수 있는 노드를 저장하기 위한 큐 (Queue queue)

인접 행렬


public boolean[] visited;
public int[][] graph;

public void bfs(int node) {
    Queue<Integer> queue = new <Integer>LinkedList();

    queue.add(node);
    visited[node] = true;

    while (!queue.isEmpty()) {
        int visitNode = q.poll();

        for (int i = 0; i < graph[visitNode].length; i++) {
            if (graph[visitNode][i] == 1 && visited[i] == false) {
                queue.add(i);
                visited[i] = true;
            }
        }
    }
}

// 그래프가 disconnected 이거나 방향그래프여서 모든 노드가 방문 불가능할때, 모든 노드 방문 시키기
public void bfsAll() {
    for (int i = 0; i < graph.length; i++) {
        if (visited[i] == false) {
            bfs(i);
        }
    }
}

인접 리스트


public boolean[] visited;
public ArrayList<ArrayList<Integer>> graph;

public void bfs(int node) {
    Queue<Integer> queue = new <Integer>LinkedList();

    queue.add(node);
    visited[node] = true;

    while (!queue.isEmpty()) {
        int visitNode = q.poll();

        for (int connectedNode : graph.get(visitNode)) {
            if (visited[connectedNode] == false) {
                queue.add(connectedNode);
                visited[connectedNode] = true;
            }
        }

        // 위 for문은 아래와 같은 의미이다.
        ArrayList<Integer> connectableNodeList = graph.get(visitNode);
        for (int i = 0; i < connectableNodeList.size(); i++) {
            int connectedNode = connectableNodeList.get(i);
            if (visited[connectedNode] == false) {
                queue.add(connectedNode);
                visited[connectedNode] = true;
            }
        }
    }
}

// 그래프가 disconnected 이거나 방향그래프여서 모든 노드가 방문 불가능할때, 모든 노드 방문 시키기
public void bfsAll() {
    for (int i = 0; i < graph.size(); i++) {
        if (visited[i] == false) {
            bfs(i);
        }
    }
}

의사코드

// 너비 우선

BFS (G, s) // 그래프 G와 출발 코드 s
    Q <= 0; // Q에는 현재 아무 노드들도 들어가 있지 않는 상태 (초기)
    Enqueue(Q, s); // Q에 출발 코드 S를 input
    while Q != 0 do // Q에 더이상 아무 노드들이 없을때까지 루프
        u <= Dequeue(Q) // Q에서 노드를 빼서
        for each v adjacent to u do // u의 인접한 노드 v들을 순회한다.
            if v is unvisited then // u의 인접한 노드 v가 방문하지 않았던 노드라면,
                mark v as visited; // v를 방문했다는 표시를 하고
                Enqueue(Q, v); // Q에 노드 v를 집어 넣는다.
            end.
        end.
    end.

참고 - gitbook

Jake

이전 포스트

알고리즘 - BFS 너비 우선 탐색

알고리즘

핵심이론

시간복잡도

구현

백준 1517 - 버블 소트

0개의 댓글

관련 채용 정보