깊이 우선 탐색 DFS 는 그래프 완전 탐색 기법 중 하나입니다 깊이 우선 탐색은 그래프의 시작노드에서 출발하여 탐색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘입니다
아래 사진을 통해 쉽게 이해해보겠습니다
DFS(깊이 우선 탐색) vs BFS(너비 우선 탐색)
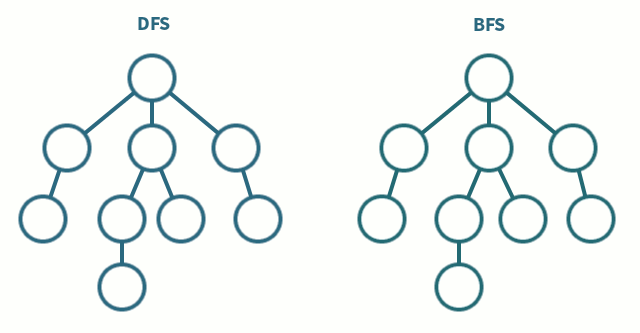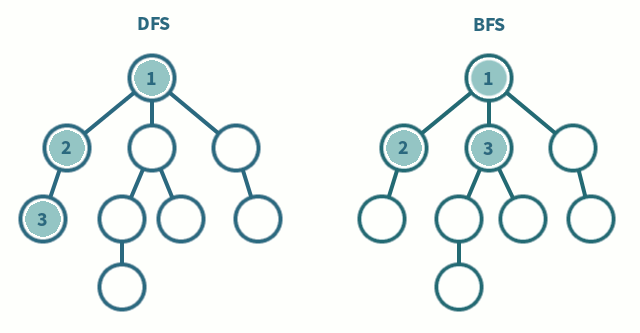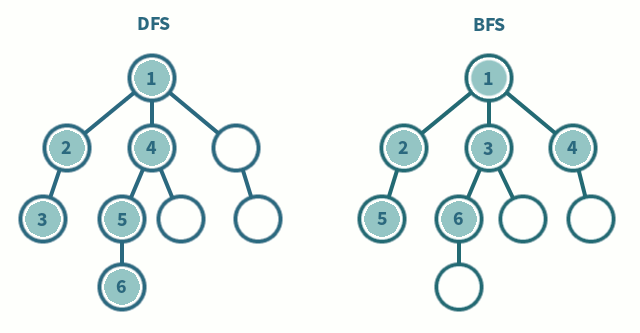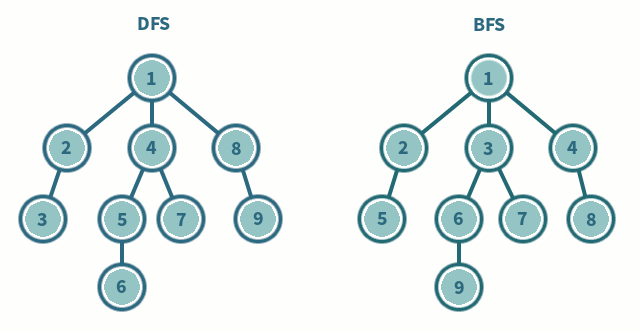
사진출처 - DFS
핵심이론
DFS는 한 번 방문한 노드를 다시 방문하면 안되므로 방문 여부를 체크할 배열이 필요하며, 그래프는 인접행렬, 인접 리스트 2가지중 하나로 표현할 수 있습니다
DFS의 탐색 방식은 후입선출LIFO 특성을 가지므로 스택을 사용해서 설명합니다
깊이 우선 탐색은 아래 순서로 진행되며 2번이 핵심 이론입니다
- DFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
- 스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 삽입하기
- 스택 자료구조에 값이 없을 때까지 반복하기
2번에서 꺼낸 노드의 인접 노드를 다시 스택에 삽입할 시 체크해야할 부분이 있습니다
스택에 노드를 삽입할 때는 해당 노드가 그 전에 방문하였는지를 방문배열을통해 체크하고, 스택에서 노드를 뺄 때 탐색 순서에 기록합니다
따라서 이전에 방문을 하였다면 스택에 삽입하지 않고 다음 인접노드를 탐색합니다
시간 복잡도
O(N^2)
최악의 경우 N^2의 복잡도입니다
- 가지치기를 이용해서 잘라내기를 하면, 해당 노드의 자식이 모두 잘라지는 효과 있음 (복잡도를 줄일 수 있음)
- 그래프의 표현을 인접 행렬 O(V^2) 대신, 인접 리스트 사용시 O(V + E)로 줄일 수 있습니다
- V: 정점(Vector), E: 간선(Edge)
깊이 우선 탐색은 실제 구현 시 재귀 함수를 이용하므로 stack overflow에 유의해야 합니다
깊이 우선 탐색을 응용하여 풀 수 있는 문제는 단절점 찾기, 단절선 찾기, 사이클 찾기, 위상정렬 등이 있습니다
구현코드
인접행렬
public boolean[] visited;
public int[][] graph;
public void dfs(int node) { // node == node index
visited[node] = true;
for (int i = 0; i < graph[node].length; i++) {
if (graph[node][i] == 1 && visited[i] == false) {
dfs(i);
}
}
}
// 그래프가 disconnected 이거나 방향그래프여서 모든 노드가 방문 불가능할때, 모든 노드 방문 시키기
public void dfsAll() {
for (int i = 0; i < graph.length; i++) {
if (visited[i] == false) {
dfs(i);
}
}
}
- 출발점이 정해져있을 경우 dfs(출발 index)로 호출 가능
- 그래프와 같이 여러 출발점이 있을 경우, visited[] 의 배열에서 탐색되지 않은 지점부터 다시 dfs()를 호출해야 모든 노드 탐색 가능
인접리스트
public boolean[] visited;
public ArrayList<ArrayList<Integer>> graph;
public void dfs(int node) { // node == node index
visited[node] = true;
ArrayList<Integer> connectNodeList = graph.get(node);
for (int i = 0; i < connectNodeList.size(); i++) {
int connectNode = connectNodeList.get(i);
if (visited[connectNode] == false) {
dfs(connectNode);
}
}
}
public void dfsSimple(int node) { // node == node index
visited[node] = true;
for (int connectNode: graph.get(node)) { // graph.get(node) => ArrayList가 나오고 이걸 for로 돔.
if (visited[connectNode] == false) {
dfs(connectNode);
}
}
}
// 그래프가 disconnected 이거나 방향그래프여서 모든 노드가 방문 불가능할때, 모든 노드 방문 시키기
public void dfsAll() {
for (int i = 0; i < graph.length; i++) {
if (visited[i] == false) {
dfs(i);
}
}
}참고 - gitbook
