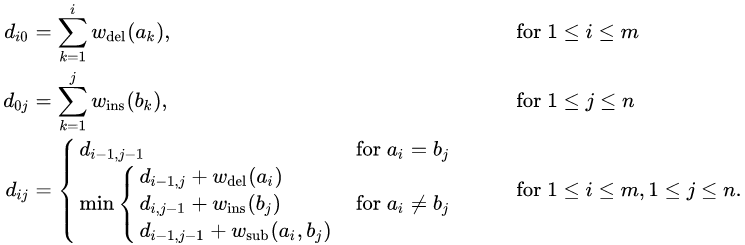편집 거리

개념

In computational linguistics and computer science, edit distance is a string metric(측정법), i.e. a way of quantifying how dissimilar two strings (e.g., words) are to one another, that is measured by counting the minimum number of operations required to transform one string into the other.
출처 : https://en.wikipedia.org/wiki/Edit_distance

편집거리는 말그대로 하나의 문자열을 다른 문자열로 '편집'하기 위한 거리=비용을 계산하므로써 두 문자열이 얼마나 다른지(=같은지)를 판단하는 알고리즘이다.

정의에서 알 수 있듯 문자열끼리의 유사성을 판단하기 때문에, 자연어 처리에서 스펠링 체크를 하거나, 생물정보학에서 염기서열의 유사성을 판단는데 쓰이기도 한다.

스펠링 체크의 좋은 예.

종류

편집의 종류에는 크게 3가지가 있다. 삽입(Insertion), 삭제(Deletion), 대체(Substitution).

1. Insertion of a single symbol.
   If $a = uv$, then inserting the symbol $x$ produces $uxv$.
   This can also be denoted $ε→x$, using $ε$ to denote the empty string.
2. Deletion of a single symbol changes $uxv$ to $uv (x→ε)$.
3. Substitution of a single symbol $x$ for a symbol $y ≠ x$ changes $uxv$ to $uyv (x→y)$.

이들 중에 어떤 편집연산을 허용하는 지에 따라 Edit Distance 알고리즘의 종류가 파생된다.

• The Levenshtein distance allows deletion, insertion and substitution.
• The longest common subsequence (LCS) distance allows only insertion and deletion, not substitution.
• The Hamming distance allows only substitution, hence, it only applies to strings of the same length.
• The Damerau–Levenshtein distance allows insertion, deletion, substitution, and the transposition of two adjacent characters.
• The Jaro distance allows only transposition.

이 글에서는 삽입, 삭제, 대체를 허용하는 Levenshtein distance의 알고리즘과,
삽입, 삭제만을 허용하는 longest common subsequence (LCS) distance 알고리즘을 알아본다.

예시

먼저 간단한 편집 예시를 통해 둘을 비교해보자.
일단 여기서는, 각각의 알고리즘을 통해 최소한의 편집횟수를 구하고자 한다.

The Levenshtein distance
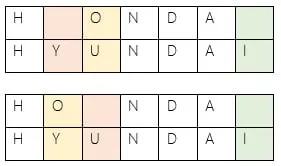
"kitten" ➡️ "sitting" distance is 3.

1. kitten → sitten (substitute "s" for "k")
2. sitten → sittin (substitute "i" for "e")
3. sittin($ε$) → sitting (insert "g" at the end)

LCS distance
"kitten" ➡️ "sitting" distance is 5.

1. kitten → ($ε$)itten (delete "k" at 0)
2. ($ε$)itten → sitten (insert "s" at 0)
3. sitten → sitt($ε$)n (delete "e" at 4)
4. sitt($ε$)n → sittin (insert "i" at 4)
5. sittin($ε$) → sitting (insert "g" at 6)

이처럼 두 알고리즘의 결과가 다른데, 쓰임새가 서로 조금씩 다르다.

• 리벤슈타인의 편집거리는 edit distance의 대표격으로 사용되는 경우가 많다.
  각 연산의 cost를 다르게 하여 가장 비용이 적게 드는 편집의 비용=거리을 구할 수도 있다.
• LCS 편집거리는 도출된 편집거리 그 자체보다는, 해당 과정을 통해 얻을 수 있는 두 문자열간의 '최장 공통 부분 수열'의 길이와 그 수열을 구할때 사용된다.

리벤슈타인의 편집거리를 먼저 알아보자.

Levenshtein distance

S = 'strong' ➡️ T = 'stone'의 경우를 예로 들어보자.
만일 각 접두부(prefix)에 대해 편집거리를 미리 알고 있다면,
예를 들어 'stro' ➡️ 'sto'의 편집거리를 미리 알고 있다면 남은 문자열('ng'와 'ne')에 대한 편집거리를 찾음으로써, 주어진 입력값 전체에 대한 편집거리를 구할 수 있을 것이다.

예상대로 DP 를 통해 부분문제를 해결해 나가면서 계산된다. 부분문제의 정의는 다음과 같다.

$E[i,j]$ 는 $S$의 앞에서부터 $i$개의 문자를, $T$의 앞에서부터 $j$개의 문자로 변환시키는 데 필요한 최소 편집거리이다.

$E[4,3]$ ('stro' ➡️ 'sto') 를 구하려고 한다면 다음의 3가지 경우를 살펴볼 수 있다.

1. $E[4,2]$ ('stro' ➡️ 'st')의 값을 알고있다면, 다시 말해 'stro'를 'st'로 바꾸는 최소의 편집거리를 이미 알고있다면, 그 편집거리에 삽입 연산의 비용 하나만 추가해주면 된다.
   'stro' ➡️ 'st' 한 후, T쪽에 'o'하나만 삽입해 주면 되기 때문이다.
   
   
2. $E[3,3]$ ('str' ➡️ 'sto')의 값을 알고있다면, 다시 말해 'str'를 'sto'로 바꾸는 최소의 편집거리를 이미 알고있다면, 그 편집거리에 삭제 연산의 비용 하나만 추가해주면 된다.
   S쪽 'stro'의 'o'하나만 빼준 상태에서 'str' ➡️ 'sto' 하면 되기 때문이다.
   
   
3. $E[3,2]$ ('str' ➡️ 'st')의 값을 알고있다면, 기존 S의 끝문자를 기존 T의 끝문자로 대체하는 편집 비용을 추가해주면된다. 'str' ➡️ 'st' 하고 해당 대체를 진행하면 되기 때문이다. 여기서는 'o'를 'o'로 대체하는 비용, 즉 0을 추가하게 된다. 가만히 둬도 되기 때문.

이를 도식화 해보면 아래와 같다.

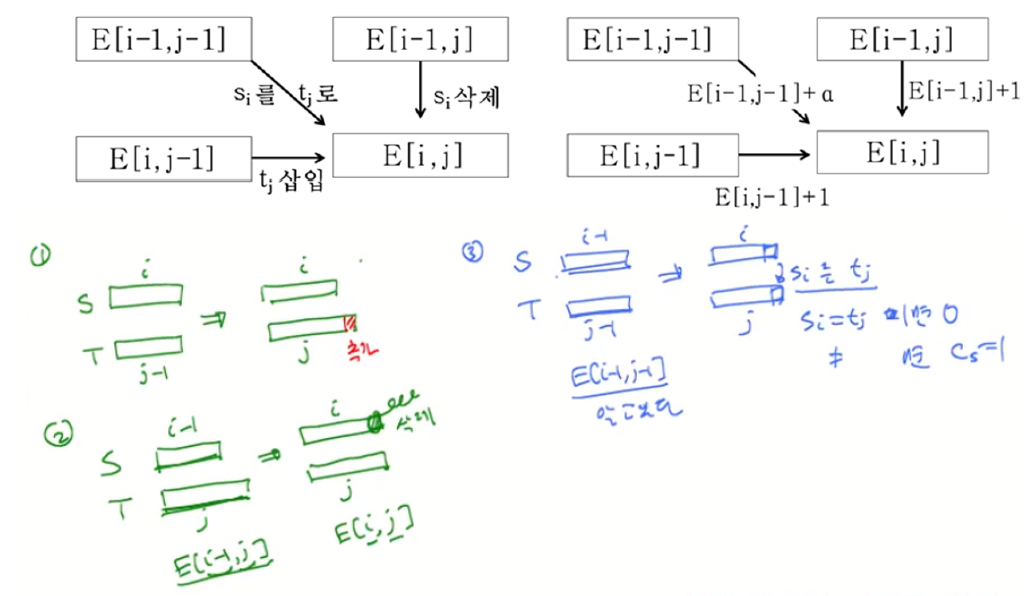
이제 이러한 특성을 이용해 dp테이블을 채워 나가면서 전체 입력에 대한 해를 구해보자.
아래는 점화식과 전체적인 코드의 진행이다.
처음 테이블의 초기화는 다음과 같이 하면 된다.

S = 기존 문자열, T = 목표 문자열, m = S의 길이, n = T의 길이

• 𝐸[𝑖,0] = 𝑖, 𝐸[0,𝑗] = 𝑗 for 𝑖 = 0,1,…,𝑚 and 𝑗 = 0,1,…,𝑛
• For 𝑖 = 1,2,…,𝑚 and 𝑗 = 1,2,…,𝑛
  𝐸[𝑖, 𝑗] = min{ 𝐸[𝑖 - 1, 𝑗] + 1, 𝐸[𝑖, 𝑗 - 1] + 1, 𝐸[𝑖 − 1, 𝑗 − 1] + 𝛼}
  where 𝛼 = 1 if $S_𝑖=T_𝑗$ 0 otherwise
  
  (아래는 대체연산이 가능하다면 다른 방향들과의 비교 없이 무조건 대체연산으로 진행하는 점화식. 이 방식을 사용하면 LCS와의 호환이 가능하다. 즉 리벤슈타인으로 계산을 하고 back-tracing으로 LCS의 길이를 오답없이 구할 수 있다.)
  

for i 0 to m E[i, 0] = i 	// 0 번 열의 초기화
for j= 0 to n E[0 ,j] = j 	// 0 번 행의 초기화

for i 1 to m
	for j= 1 to n
		E[i, j] = min{E[i,j-1] + 1 , E[i-1 ,j] + 1 , E[i-1,j-1] + a}
        									
return E[m, n]

dp

m*n 크기의 테이블을 하나씩 채워나가야 하므로 시간 복잡도는 $Θ(mn)$이 된다.

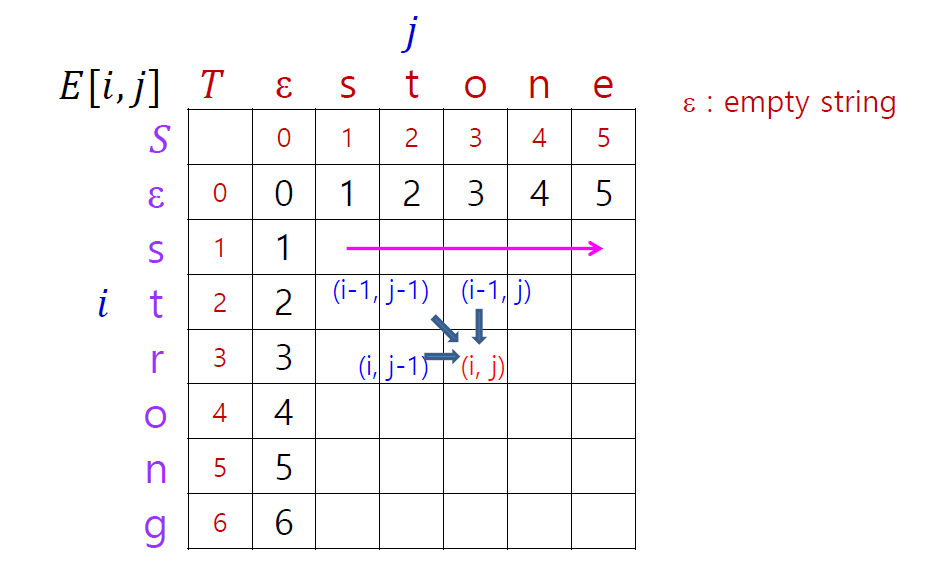
$ε$에서 T의 각 부분 문자열('s','st, ... ,'stone')로 편집하는 비용은 그냥 그 문자열의 길이만큼 삽입해주는 비용이다. 따라서 j = 1,2,...,T의 길이 일때 E[0,j] = j 이다.
마찬가지로 S의 각 부분 문자열에서 $ε$로 편집하는 비용은 그 문자열의 길이만큼 삭제 해주는 비용이다. 따라서 i = 1,2,...,S의 길이 일때 E[i,0] = i 이다.

이후에 점화식에 따라 테이블을 채워나가다보면, dp[m][n]이 전체 입력값에 대한 최소 편집 거리가 된다.

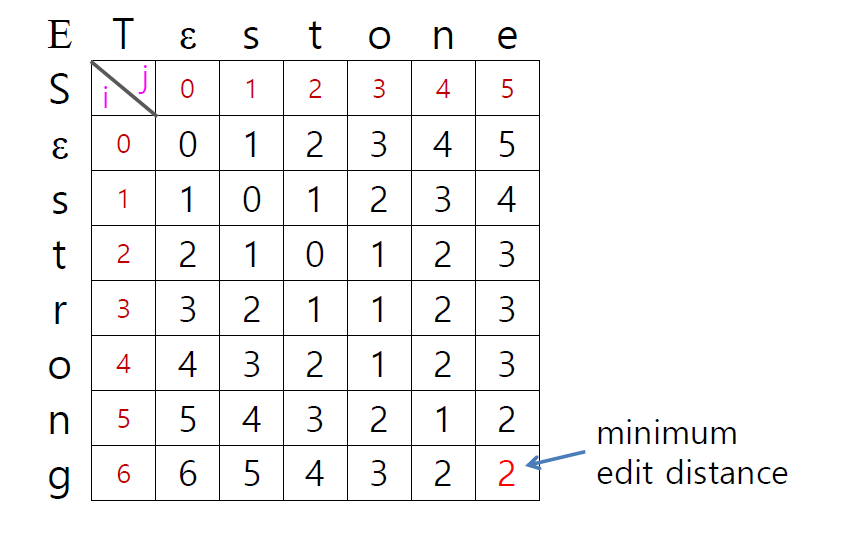
back-tracing

최소 편집거리 값 뿐만 아니라, 각 과정에서의 연산의 종류도 확인할 수 있다. 다만 최종 결과를 구한 후 계산 과정을 거슬러 올라가면서(back-tracing) 각 연산의 종류를 파악해야 한다.

최종 인덱스 (m,n)부터 시작해 이전의 세 방향 중에서 최소값이 어느 방향으로부터 왔는지를 체크하면서 연산의 종류를 알아낸다.

아래는 이와 같은 방법으로 여러 테스트케이스의 최소 편집 비용과 연산 과정을 나타낸 결과이다.

LCS(Longest Common Subsequence) distacne

리벤슈타인의 편집거리 계산과의 차이점은 대체연산을 허용하지 않는다는 점이다.
하지만 대체연산을 허용하지 않는 것이 연산의 종류를 한정시키기 위함이라기 보다,
LCS distacne를 통해 얻고자 하는 결과를 위해 대체연산을 특별취급 하는 것이다.
LCS distacne를 통해 얻고자 하는 것은 '최장 공통 부분 수열의 길이'와 그 '수열'이다.
따라서 리벤슈타인 편집거리의 과정과 매우 유사하게 동작하면서도,
'비용이 들지 않는 대체연산'의 개수와, 해당 연산의 대상이 되었던 문자를 알아내고자 하는 것이 이 알고리즘의 목표라고 할 수 있다.

점화식을 먼저 살펴보자.

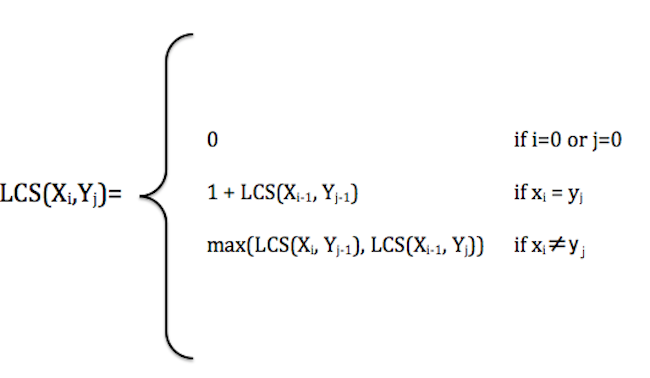
위에서 언급했듯, 편집거리 자체를 계산하는 것이 주 목적이 아니므로, 허용된 연산(삽입, 삭제)에 대한 비용 계산이 없다. 다만 $x_i = y_i$의 경우, 즉 '비용이 들지 않는 대체연산'이 가능한 경우에 1을 더해줌으로써 공통 부분 수열의 길이를 1늘리고, $x_i = y_i$의 경우 해당 연산이 불가능 하므로, 삽입 삭제 중에서 하나를 고르는데, 이 중 max값을 선택해 공통 부분 수열의 길이가 최장으로 유지될 수 있도록 하는 것이다.
아래는 이에 대한 의사코드.

function LCSLength(X[1..m], Y[1..n])
    C = array(0..m, 0..n)
    for i := 0..m
        C[i,0] = 0
    for j := 0..n
        C[0,j] = 0
    for i := 1..m
        for j := 1..n
            if X[i] = Y[j]
                C[i,j] := C[i-1,j-1] + 1
            else
                C[i,j] := max(C[i,j-1], C[i-1,j])
    return C[m,n]

dp

이러한 원리로 R = 'GAC', C = 'AGCAT' 에 대한 LCS를 구한다고 했을 때,
완성된 dp테이블은 다음과 같다.

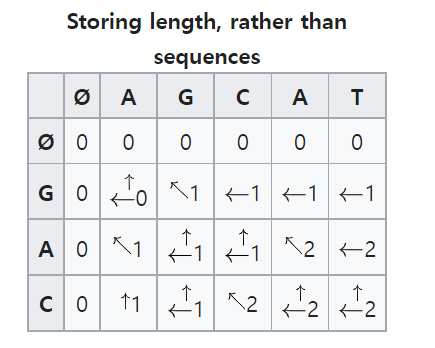
테이블 마지막 셀에 있는 2가 LCS의 길이가 된다.

back-tracing

그 수열을 직접 구하고자 할때는, 역시 back-tracing을 이용한다.

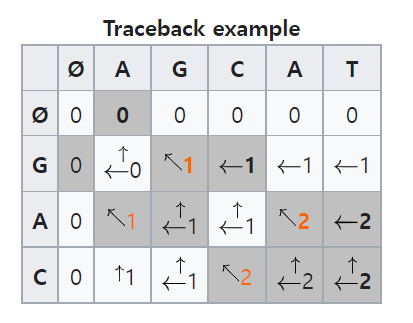
'비용이 들지 않는 대체 연산'이 현재 인덱스에서 가능한지 확인한다. 위에서는 주황색으로 표시된 인덱스가 해당된다.
가능하다면 LCS에 추가하고, 불가하다면 삽입(한칸 왼쪽), 삭제(한칸 위)중 최대값을 찾아 다시 진행한다.
단, LCS가 여러개 일 수도 있기 때문에 하나의 LCS를 읽어낼 때와, 모든 LCS를 전부 찾을 때의 코드가 다르다.

• 하나만 읽어내는 경우
  현재 인덱스의 두 문자 (X[i]와 Y[j])가 같다면( = '비용이 들지 않는 대체 연산'이 현재 인덱스에서 가능하다면) 그 문자는 LCS안에 포함되어 있을 것이다. 따라서 결과 값에 추가해준다.
  두 문자가 같지 않다면, 위쪽 값과 아랫쪽 값 중 큰 값을 찾아서 LCS의 길이가 최대가 되게 유지해주면서 이동한다. 위쪽 값과 아랫쪽 값이 같다면 LCS가 여러개 존재한다는 신호인데, 지금은 하나만 읽어내는 경우 이므로 아무거나 선택하면 된다. 위의 그림에서는 bold처리된 path가 현재 읽어내는 하나의 LCS이다.

function backtrack(C[0..m,0..n], X[1..m], Y[1..n], i, j)
    if i = 0 or j = 0
        return ""
    if  X[i] = Y[j]
        return backtrack(C, X, Y, i-1, j-1) + X[i]
    if C[i,j-1] > C[i-1,j]
        return backtrack(C, X, Y, i, j-1)
    return backtrack(C, X, Y, i-1, j)

• 모든 LCS를 읽어내는 경우
  하나만 읽어내는 경우와 유사하지만,
  X[i]와 Y[i]가 같지 않은 상황에서 위쪽 값과 아랫쪽 값이 같다면, 둘다 탐색하러 들어감으로써 모든 LCS를 읽어낸다. 지수시간이 걸릴 수 있다.

function backtrackAll(C[0..m,0..n], X[1..m], Y[1..n], i, j)
    if i = 0 or j = 0
        return {""}
    if X[i] = Y[j]
        return {Z + X[i] for all Z in backtrackAll(C, X, Y, i-1, j-1)}
    R := {}
    # C[i-1,j] == C[i,j-1]인 경우 아래의 a,b 둘다 만족해 둘다 실행된다.
    # 한쪽이 클경우 a와 b 중 하나만 실행된다.
    if C[i,j-1] ≥ C[i-1,j]						# a
        R := backtrackAll(C, X, Y, i, j-1)
    if C[i,j-1] ≤ C[i-1,j]						# b
        R := R ∪ backtrackAll(C, X, Y, i-1, j)	# a가 실행되었을 때를 대비하여 R과 합쳐준다.
        									
    return R

참고사이트

https://en.wikipedia.org/wiki/Edit_distance
https://en.wikipedia.org/wiki/Longest_common_subsequence_problem