MST (Minimum Spanning Tree)

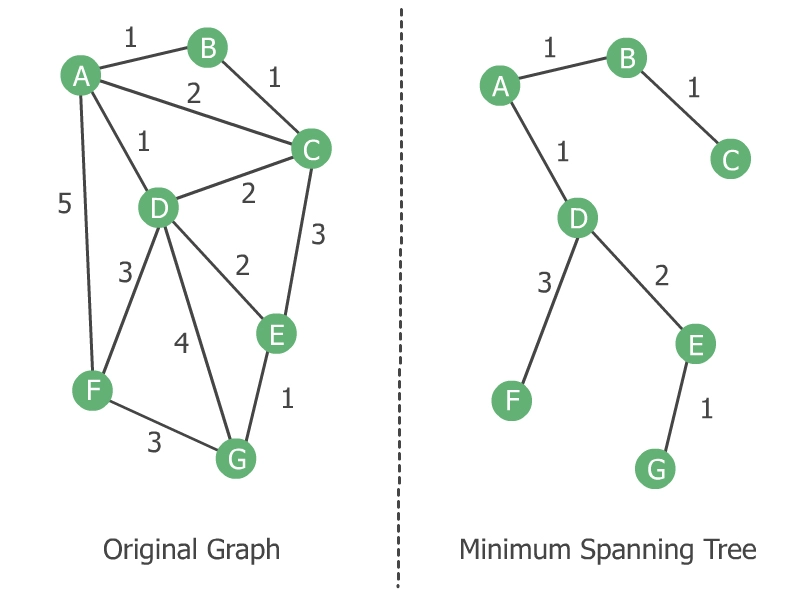
Given an undirected weighted graph, a minimum spanning tree (MST) is a subgraph that connects all the vertices with the lowest possible sum of its edge weights.

방향성이 없고 가중치가 있는 그래프에서, 가장 최소한의 가중치로 모든 정점을 연결할수 있는 subgraph를 의미.

Shortest Path

Given a weighted graph, the shortest path (or geodesic path) between two vertices is a path with the lowest possible sum of edge weights.

방향성은 무관. 가중치가 있는 그래프에서, 두 정점 사이를 잇는 가장 적은 가중치의 경로를 의미.

위의 그림과 같이, Shortest path는 그래프의 모든 정점을 포함하지 않을 수도 있다.

Prim vs Dijkstra

세 가지 정도의 차이점으로 요약할 수 있다.

1. Dijkstra’s algorithm finds the shortest path, but Prim’s algorithm finds the MST.
   Dijkstra는 최단경로를, Prim은 최소 신장 트리를 찾아준다.
   어느 한 쪽이 다른 한 쪽을 보장해 줄 수 없다.
   
   
2. Dijkstra’s algorithm can work on both directed and undirected graphs, but Prim’s algorithm only works on undirected graphs.
   Prim은 무방향 그래프에서만 동작한다. Dijkstra는 상관없다.
   
   
3. Prim’s algorithm can handle negative edge weights, but Dijkstra’s algorithm may fail to accurately compute distances if at least one negative edge weight exists.
   Prim은 음의 가중치를 가진 간선에서도 잘 동작한다. Dijkstra는 이상한 결과가 나올 수도 있다.

구현에서

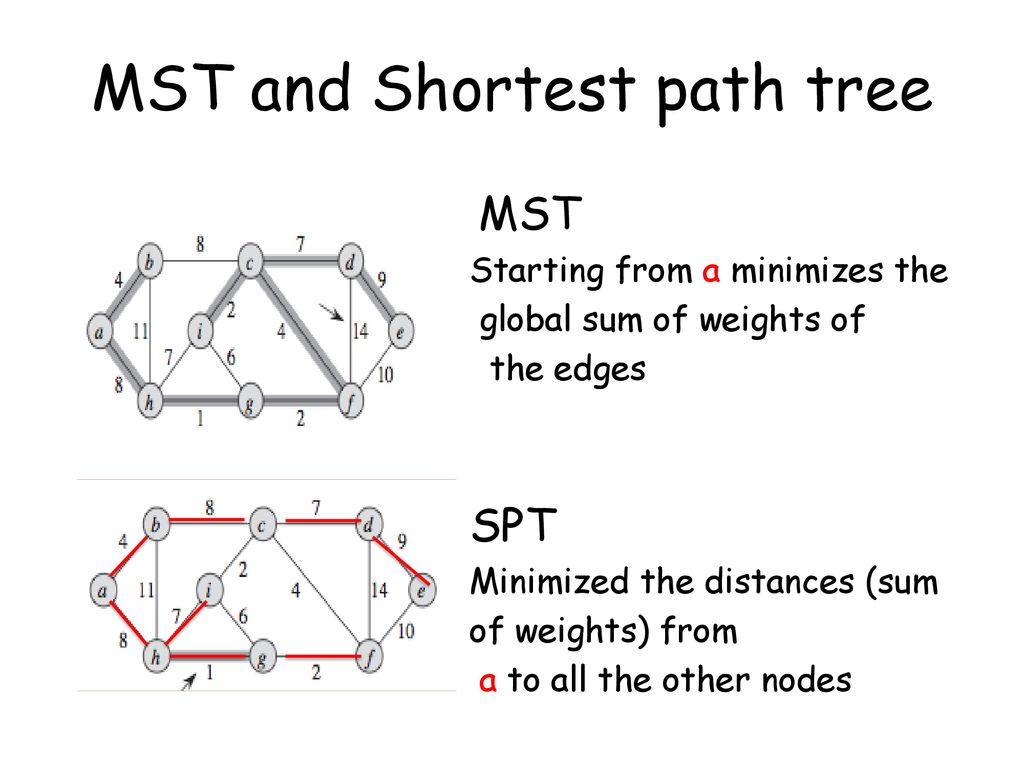
다음 그림을 보자. Dijkstra 알고리즘을 설명하는 그림이다.

지금 Y(완료된 정점 집합)에 정점 E 까지 추가된 상황. 그 이후의 B 정점에 대한 distance의 갱신을 하고자 한다.

• Prim -> 기존 distance = 7 과, 새로운 distance = 2 (E와 인접하게 됨으로써 얻어지는) 와의 비교.
• Dijkstra -> 기존 distance = 7 과, 새로운 distance = 5 (E를 거쳐서 올 수 있는 것으로 부터 얻어지는) 와의 비교.

이 차이의 근본적 원인은 prim은 그저 스패닝 트리를 최소한의 거리 만큼씩만 확장하려고 하는 것이고,
dijkstra는 어떠한 출발점(source)으로부터 각 정점에 대한 최소 거리를 구하려고 하는 것이기 때문이다.

참고로 알아둘 것은, Prim 이든 Dijkstra든 heap을 통해 최소값을 얻고자 할 때는
heap에 이전 distance에 대한 정보들이 죽지 않고 남아있다는 점을 조심해야 한다는 것.

배열로 distance 정보를 저장하고 갱신한다면 이전 distance들이 새로운 distance로 대체되기 때문에 살아남지 못하지만, 힙은 최소값만 뽑아오는 원리라서 이전 정보가 남아있을 수 있다.

위의 그림에서는 B를 Y에 넣고 나서(Prim)/최소거리가 확정되고 나서(Dijk.),
A와 B를 연결한 가중치 7의 간선이 heap에 계속 남아있게 된다.

따라서 아래의 코드와 같이 heappop을 해줄 때 조건을 주어야 한다.

Dijkstra

# Dijkstra
#
# distance 배열은 항상 distance에 대한 최신 정보를 가지고 있다.
# heap을 따로 쓰는 이유는 distance 배열을 선형탐색해 최소값을 찾는 번거러움을 덜기 위해.
# 그래서 distance_heap은 distance 배열의 최신 정보를 가지면서도, 이전 단계의 distance정보도 남아 있을 수 있다.
# 그래서 a에서 최신의 정보인지 확인을 해준다. distance는 생각해보면 줄어들면 줄어들었지 늘진 않는다. (항상 최소값으로 갱신하려고 함.)
# 따라서 distance_heap에서 꺼낸 v에 대한 dist정보가, distance배열의 해당 값보다 '크다면' 이미 이전 단계의 정보인 (visited된) 것이다.
# 그래서 continue를 통해 heap의 다음 최소값으로 넘어간다.
while distance_heap:
    dist, v = heappop(distance_heap)
    if distance[v] < dist:        # (a) visited check.
        continue
    # visited check를 통과한 정보의 v는 최신의 distance정보(Y 에서 다른 정점의 거리)에서 최소값을 가진 정점이다.
    # 이제 v는 Y에 들어온 것이다.
    ...

Prim

# Prim
while distance:
        if (e := heappop(distance))[1] not in Y:    # 이전 distance정보들이 heap에 계속 남아있기 때문에
                                                    # Y집합을 향하지 않는 엣지가 나올 때 까지 pop 한다.
                                                    # 배열을 쓴다면 배열은 배열 값 자체를 갱신해주기 때문에 이전 distance정보가 남을 수 없을 것.
            Y.add(e[1])  #  vertex
            cost += e[0] #  weight
            next = e
            break
       ...

참고사이트

https://www.baeldung.com/cs/prim-dijkstra-difference