선형 회귀 (Linear Regression)

우리는 위의 표와 같은 데이터를 가지고 있으면 이 표를 그래프로 표시할 수 있습니다.

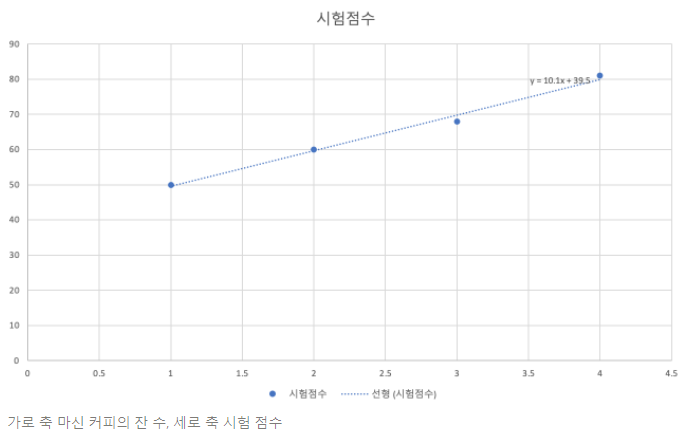
중요)

우리는 이 그래프를 보고 가설을 세울 수 있습니다. 임의의 직선 1개로 이 그래프를 비슷하게 표현할 수 있다고 가설을 세울 수 있습니다. 이 선형 모델은 수식으로 아래와 같이 표현할 수 있습니다.(직선 = 1차함수)

중요)

우리는 정확한 시험 점수를 예측하기 위해 우리가 만든 임의의 직선(가설)과 점(정답)의 거리가
가까워지도록 해야합니다. (=mean squared error)

[개인 메모]정확한 점수를 예측하기 위해 내가 만든 가설과 정답의 거리가 가까워 져야합니다.

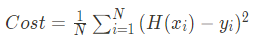
중요)

여기서 H(x)는 우리가 가정한 직선이고 y는 정답 포인트라고 했을 때 H(x)와 y의 거리(또는 차의 절대값)가 최소가 되어야 이 모델이 잘 학습되었다고 말할 수 있습니다.

중요)

여기서 우리가 임의로 만든 직선H(x)를 가설(Hypothesis)이라고 하고 Cost를 손실 함수(Cost or Loss function)라고 합니다.

다중 선형 회귀(Multi-variable linear regression)

위에서는 마신 커피 잔 수만 입력값으로 들어갔지만 만약 입력값이 2개 이상이 되는 문제를 선형 회귀로 풀고 싶을때 다중 선형 회귀를 사용합니다.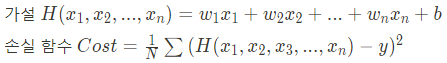

후기

처음 배워보는 머신러닝이였습니다. 처음에는 이게 무슨 소리지.. 하고 이해가 하나도 안되어서
힘들었지만 이해를 하기위해서 강의를 계속 돌려보고 이렇게 작성을 해보니 선형 회귀에 대해서는
이해가 된거같습니다. 제일 생각 나는 부분은 제가 임의로 만든 가설과 정답의 거리가 최소가 될수록 학습이 잘 되었다는걸 알 수 있었습니다. 이부분은 꼭 기억하면서 가야겠습니다.
앞으로도 공부하고 자기개발을 해서 발전하는 개발자가 되겠습니다. 감사합니다.