컴퓨터에서 실수를 표현하는 방법은 크게 Fixed Point와 Floating Point 두 가지가 존재한다. float이라는 자료형에서 알 수 있듯이 float과 double은 floating point를 사용한다. fixed point는 소수점의 위치를 고정시켜놓고 실수를 표현하는 방식이다. 반면 floating point는 소수점의 위치를 고정시키지 않는다. 다르게 표현해서 float 즉 띄어놓고 사용하는 방식이다. 이렇게 함으로서 fixed point보다 더 넓은 범위의 수를 표현할 수 있다. 반면 fixed point는 floating point보다 속도가 빠르다는 장점이 있다.

Floating Point

부동소수점을 표현하는 방식은 IEEE 754에서 표준화 되었다.

IEEE 754 표준

이 표준에서 실수는 과학적 표기법에 의해 표현된다.

$±f\ \times\ b^e$

이 때 f는 가수 b는 밑 e는 지수이다. 컴퓨터에서는 2진수 체계를 사용하기 때문에 b는 2로 고정되어 있다. 여기서 f, e와 부호비트를 저장함으로서 컴퓨터는 실수를 표현한다.

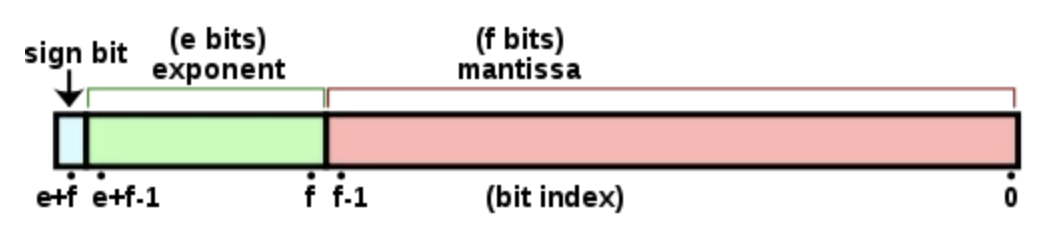
우리가 자주 쓰는 float의 경우 대략 지수부는 8비트 가수부는 23비트 부호비트로 1비트를 사용합니다. 한편 double의 경우는 가수부분이 52비트이고 지수부분이 11비트를 차지합니다. 물론 이는 시스템마다 다릅니다.

실수 표현하기

1. 우선 수의 부호를 보고 0이상이면 0 아니라면 1로 표현합니다.
2. 이후 수를 정규화합니다. 수를 정규화한다는 것은 1.xxxx형태로 만든다는 것을 의미합니다.
3. 이때 정규화 작업을 할때 얼만큼 shift되었는지를 지수부에 저장하고 정규화된 수를 가수부에 저장합니다.
4. 마지막으로 지수부에 bias처리를 해줍니다.
   1. bias 처리를 해주는 이유는 해당 지수부가 매번 양수가 아닐 수 있기 대문이다.
   2. 0.001의 경우에는 지수부가 음수가 나온다.
   3. 이렇게 모든 수를 bias 처리를 해줌으로서 해당 지수부의 크기비교를 쉽게 수행할 수 있다.
   4. 이때 bias된 지수의 범위는 1에서 254까지인데 0과 255는 특수한 상황을 나타내기 위해 사용된다.

종류	지수부	가수부
비정상수	0	0이 아님
무한대	2^e - 1	0
NaN	2^e - 1	0이 아님

비정상수

이 수들은 bias처리를 해도 해당 지수부가 양수가 되지 않은 수를 의미합니다.

무한대

부호비트 덕분에 양의 무한대와 음의 무한대를 파악할 수 있다. 연산과정에서 표현할 수 있는 수보다 큰 수가 들어갔을 때 발생함. 즉 가수부의 값을 nomalize할 때 해당 가수부를 표현할 수 있는 비트로 표현할 수 없는 경우 발생하게 된다. 즉 지수부의 최대 값을 곱해도 normalize가 불가능한 경우이다.

NaN

무한대 % 무한대, 수 % 0과 같이 엄밀하게 값을 정할 수 없는 경우 발생한다.

이렇게 하면 어떤 장점이 있을까?

이렇게 실수를 floating 한다면 어떤 장점이 있을까? 바로 굉장히 넒은 범위의 수를 표현할 수 있다는 것이다. 흔히 실수표현을 위한 자료형이라고 하지만 나는 그보다 더 넓은 범위의 표현을 가능하게 하는 자료형이라고 생각한다.
1. 정수형은 0과 1사이의 숫자를 표현하지 못한다.
- floating point를 사용함으로서 0과 1사이의 범위의 숫자를 표현해줄 수 있다.
2. 정수형이 표현해주지 못하는 굉장히 큰숫자도 표현해줄 수 있다.
- 지수부를 따로 가지고 있기 때문에 굉장히 큰 숫자도 표현해 줄 수 있다.

그렇다면 단점은?

단점은 말 그대로 숫자의 Acurracy가 낮아지게 된다. 즉 1.2라는 값이 정말 1.2와 같은 값일 수도 있지만 이와 매우 근사된 값이 있을 수 있다. 반면 precision이 높아지게 된다. 1.5라는 숫자를 int는 1혹은 2로 표현해야 하지만 float/double은 1.5에 매우 근사한 숫자로 표현할 수 있다.