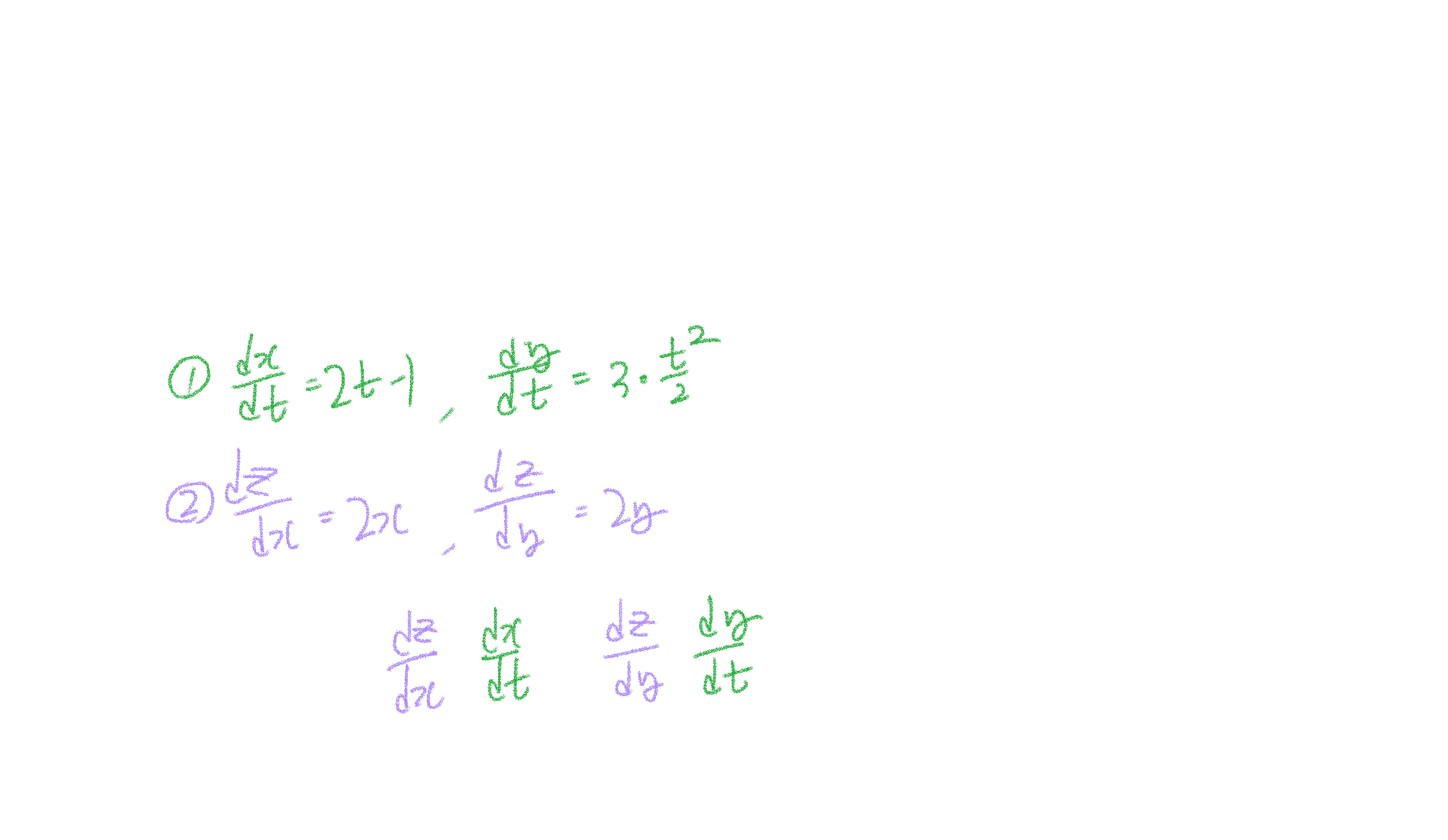Keywords

Gradient Descent (경사하강법)은 예측값과 타겟값의 차이를 최소 또는 0으로 만들기위해 사용되는 테크닉중 하나이다. (머신러닝의 기본은 최적값, Optimization을 하는 과정) 아래 키워드는 Gradient Descent를 이해하기위한 키워드를 정리한것이다.

• Objective Function
• MSE (Mean Squared Error)
• Limit of Function (함수의 극한)
• Derivative (도함수)
• Partial Derivative (편미분)
• Chain Rule (다변수 함수의 편미분, 연쇄법칙)
• Learning Rate

Objective Function

설계한 모델의 학습 성능을 평가하는 지표.

MSE

예측값과 실제값 차이를 구하는 수학적 표현.

${1\over N}\sum\limits_{n=1}^{N}(\hat y-y)^2$ | $\hat y$: 예측값, $y$: 실제값

Derivative

Partial Derivative

편미분은, 다변수 함수 $\nabla f(x)= ( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n} )$를, 각 입력에 대해 미분을 수행한다.

$z(x,y) = 2x + 3y + y^3$일때, z(x,y)를 x와 y에 대해 편미분을 해보자.

1. 함수 z를 변수 x에 대해 미분하기:
   $\frac{\partial z}{\partial x} = \frac{\partial}{\partial x}2x + \frac{\partial}{\partial x}3y + \frac{\partial}{\partial x}y^3$ = 2

2. 함수 z를 변수 y에 대해 미분하기:
   $\frac{\partial z}{\partial y} = \frac{\partial}{\partial y}2x + \frac{\partial}{\partial y}3y + \frac{\partial}{\partial y}y^3 = 0 + 3+ 3y^2 = 3y^2 +3$

미분하고자 하는 변수를 제외하고, 나머지 변수는 전부 상수 취급한다. (상수는 미분값이 0)

Chain Rule

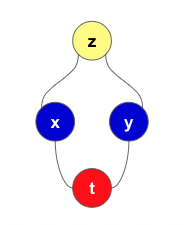
z가 x와 y에 대한 Multivariable 함수이며, x와 y가 t에 대한 함수(i.e, $z(x,y), x(t), y(t)$일때 Chain Rule이 적용된다.

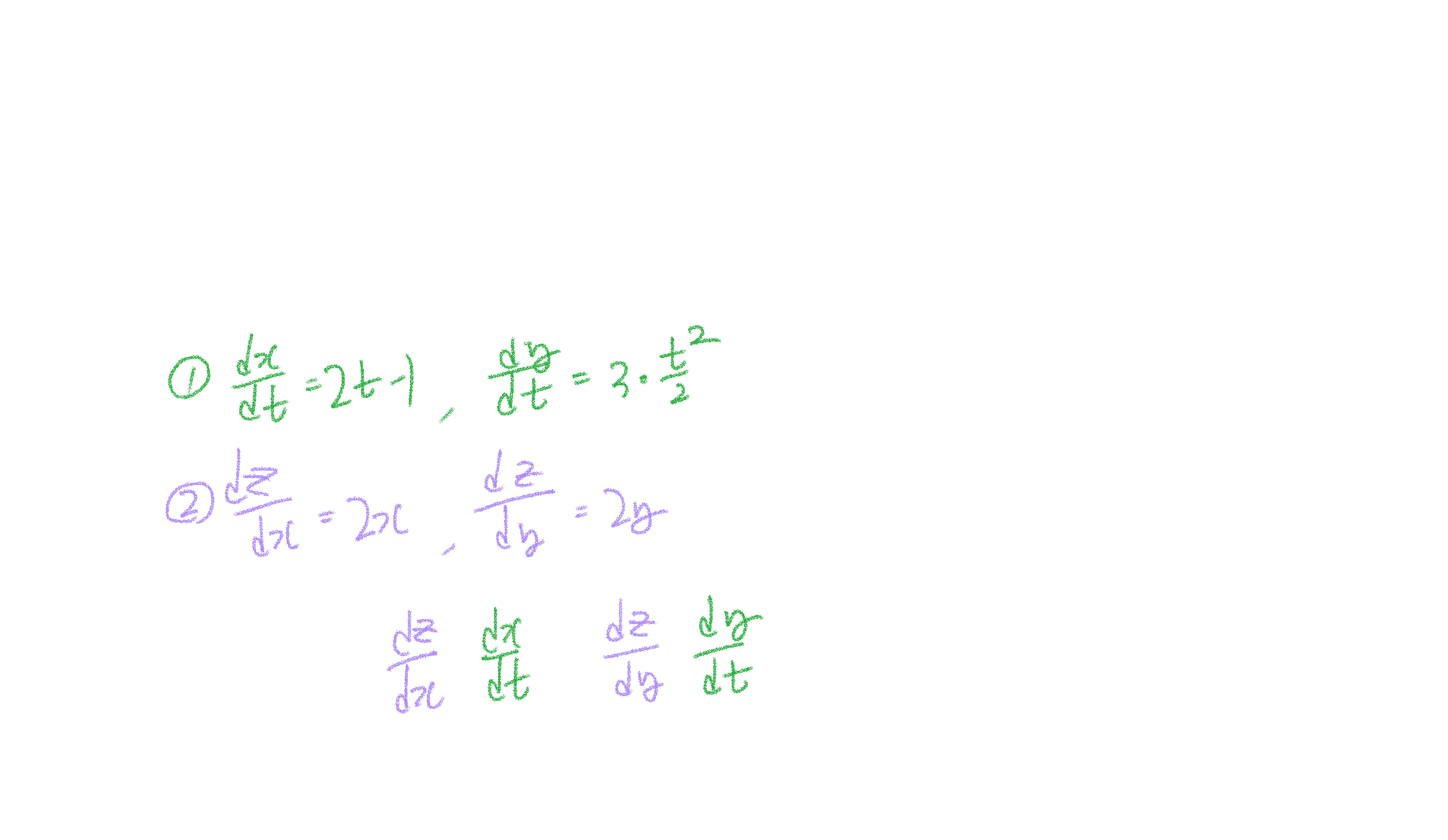
아래는 다변수 함수 z(x,y)를 t에 대해 미분 시, 관계도이다.

Gradient Descent

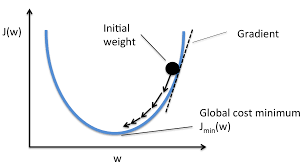
Gradient Descent는 손실함수의 국소값(Local Minimum)을 찾기위해 사용된다.

Gradient descent is based on the observation that if the multi-variable function $f(x)$ is defined and differentiable in a neighborhood of a point $a$ , then $f(x)$ decreases fastest if one goes from $a$ in the direction of the negative gradient of $F$ at $a$ ,$-\nabla f(x)$

출처: https://towardsdatascience.com/gradient-descent-demystified-bc30b26e432a#:~:text=Gradient%20descent%20is%20based%20on,F%20at%20the%20point%20x.

경사 하강법은, 다변수 함수 $f(x)$ 가 임의의 점 a에서 미분가능하며 해당 $a$지점에서 $F(x)$의 음의 경사방향으로 이동한다면($-\nabla f(x)$) $f(x)$는 가장 빠르게 감소할것이다라는 관측에 기반한 것이다.

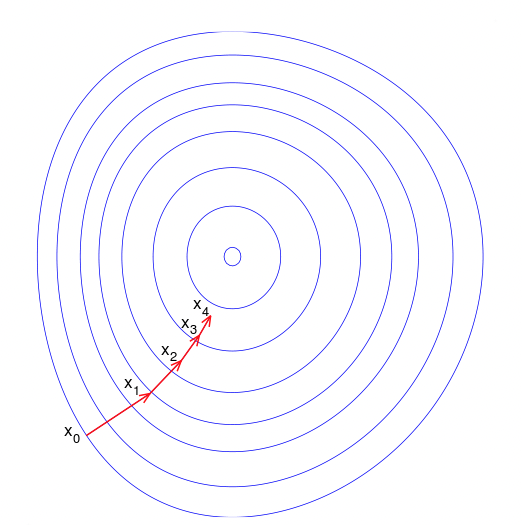
출처: https://en.wikipedia.org/wiki/Gradient_descent

해당 등고선 그래프에서 $x_i$는 그래프의 중앙값(손실 함수의 국소값)에 접근하고 있다. 빨간색 화살표는 임의의 점 a에서 기울기의 반대 방향으로 이동하는것을 보여준다.

아래는, Gradient Descent의 수학적 표기이다.

$x_{n+1} = x_n -\gamma \nabla f(x)$

$\nabla f(x)$: Gradient at $a$ (Direction and Gradient)

Gradient

각 점에서의 기울기를 구하기 위해서는, 각 점의 순간 변화량을 뜻하는 미분값을 알아야한다. 다음 직선의 방정식을 살펴보자.

$y = ax + b$

한점의 기울기를 구하기위해 다음과 같이 x에 대한 미분을 취한다.

$\frac{\partial y}{\partial x} = \frac{\partial }{\partial x}ax + \frac{\partial }{\partial x}b = a$

참고: 직선의 방정식에서, $a$ = 기울기 $b$ 는 y절편이다.

다변수 함수$f(x_1, x_2, ..x_n)$의 기울기를 구하려면, 모든 변수에 대해 미분을 해줘야하고 이때 편미분의 개념이 들어간다.

이를 $\nabla f(x)= ( \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n} )$ 으로 표현한다.

임의의 점 a에서 구한 기울기의 방향과 크기를, 해당 a 점에서 빼주게되면 그 기울기의 반대 방향만큼 이동하게 되어 결국 국소점에 도달한다는 개념이다.

MSE에 Gradient Descent 적용하기

결국, Regression문제의 최적값을 찾는 방법은 MSE의 국소점을 찾는 방법과 동일한 방법이된다.

오차함수인, MSE에서 경사하강 알고리즘을 적용하면, 아래와 같이 국소점으로 접근한다.

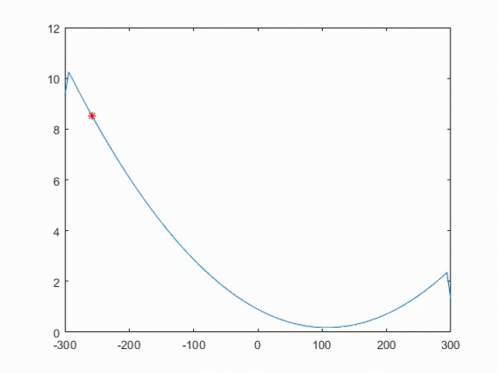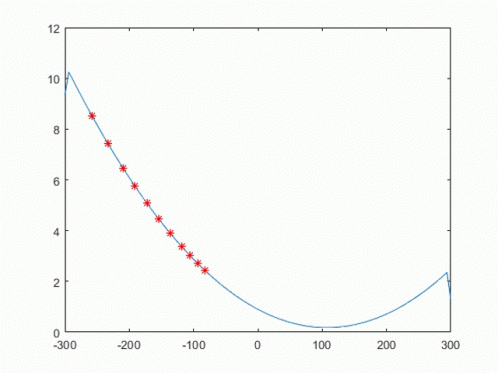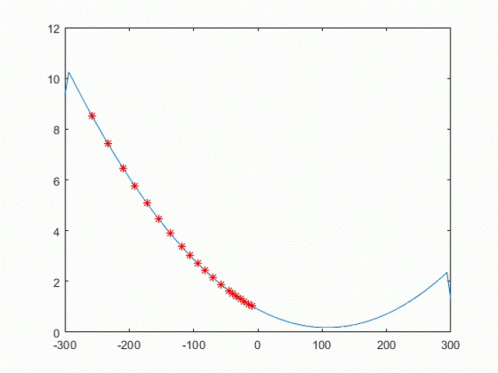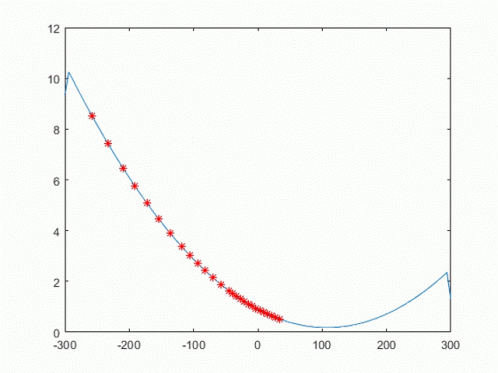
여기서 Step Size를 나타내는 $\gamma$ 또는 $\alpha$가 나오는데, 값의 국소값 근처에서 Overshooting을 억제하기 위해 사용된다.

$y = wx + b$ 라는 선형 회귀식에서 w와 b의 최적값을 찾기 위한 공식은 아래와 같다.

1. $w_{n+1} = w_n - Gradient(w)$ | n+1 번째 가중치
2. $b_{n+1} = b_n - Gradient(b)$ | n+1 번째 편차

Gradient (w) 구하기

현재 기울기($w_n$에서 기울기인 $w_{n + 1}$을 구하기 위해서, 현재 가중치인 $w_n$에서 $Gradient(w_n)$만큼 빼야한다.

1. $w$에 대해 미분한다.

   $Gradient(w_n) = \nabla {1 \over N}\sum\limits_{n=1}^{N}(error)^2$

2. $Error = y- \hat y$

   $Gradient(w_n) = \frac{\partial}{\partial w} {1 \over N}\sum\limits_{n=1}^{N}(y- \hat y)^2$

3. $y = w_nx +b_n$ 으로 치환.

   $Gradient(w_n) = \frac{\partial}{\partial w}{1 \over N}\sum\limits_{n=1}^{N}((w_n+b_n)- \hat y)^2$

4. Chain Rule 적용.

   $Gradient(w_n) = {1 \over N}\sum\limits_{n=1}^{N} 2* ((w_n+b_n)- \hat y) * x$

5. $y = w_n + b_n$이기 때문에, 식을 보기 쉽게 정리한다

   $Gradient(w_n) = {2 \over N}\sum\limits_{n=1}^{N}(y- \hat y) * x$

6. $w_{n+1}$에 적용한다.

   $w_{n+1} = w_n - \alpha*{2 \over N}\sum\limits_{n=1}^{N}(y- \hat y) * x$

즉 현재의 가중치인 $w_n$ 에서, 그에 대한 기울기 Gradient(w)를 조금씩 빼면서 MSE가 최소가되는 국소점을 찾아나간다.
여기서 $\alpha$는 앞서 말했듯이 Learning Rate로 값이 경사 하강시, 국소점 근처에서 Overshooting 을 막기위해 사용된다. 통상 1 이하의 값을 가진다.

Gradient(b) 구하기

회귀식이, $wx+b$로 정의 되기때문에 w에 대한 기울기 뿐 아니라, 편차인 b에 대한 정보도 새롭게 업데이트 해줘야한다.

Gradient(w)를 구하는 것과 마찬가지로 n+1번째 Bias를 구하기 위해서, 현재 $b_n$에서 Bias(b) 만큼 빼줘야한다.

1. $b$에 대해 미분한다.

   $Gradient(b_n) = \nabla {1 \over N}\sum\limits_{n=1}^{N}(error)^2$

2. $Error = y- \hat y$

   $Gradient(b_n) = \frac{\partial}{\partial b} {1 \over N}\sum\limits_{n=1}^{N}(y- \hat y)^2$

3. $y = w_nx +b_n$ 으로 치환.

   $Gradient(b_n) = \frac{\partial}{\partial b}{1 \over N}\sum\limits_{n=1}^{N}((w_n+b_n)- \hat y)^2$

4. Chain Rule 적용.

   $Gradient(b_n) = {1 \over N}\sum\limits_{n=1}^{N} 2* ((w_n+b_n)- \hat y)$

5. $y = w_n + b_n$이기 때문에, 식을 보기 쉽게 정리한다

   $Gradient(b_n) = {2 \over N}\sum\limits_{n=1}^{N}(y- \hat y)$

6. $w_{n+1}$에 적용한다.

   $b_{n+1} = w_n - \alpha*{2 \over N}\sum\limits_{n=1}^{N}(y- \hat y)$

MSE

새롭게 구한 $w_{n+1}$과 $b_{n+1}$에 대한, 회귀 식($y = w_{n+1} + b_{n+1}$) 에대한 Cost Function이 최적값인지 확인하고, 최적값을 찾을때까지 Gradient Descent 를 반복한다.