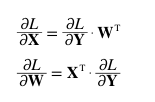
입력 신호가 행렬이고, 다음의 뉴런으로 순전파 될 때 행렬의 곱은 어떻게 처리되는지 그리고 주의해야할 점은 무엇인지 알아보도록 하자.
Affine 계층
딥러닝에서 Affine 계층은 순전파시 행렬 곱을 수행하는 계층을 의미한다. 아래는 Affine 계층에서 행렬곱이 어떻게 순전파 / 역전파가 수행되는지 보여주는 계산 그래프이다.
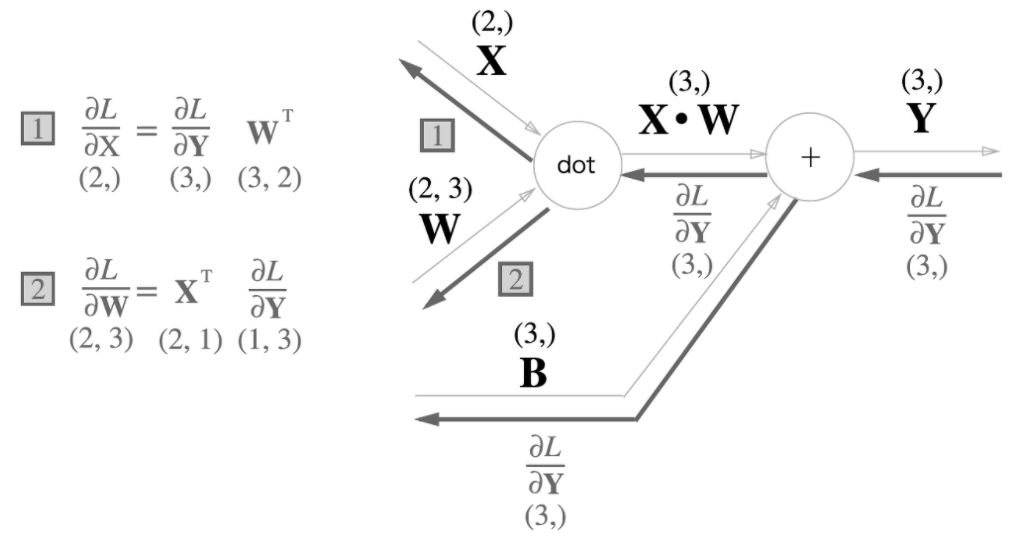
행렬의 형상(Shape)
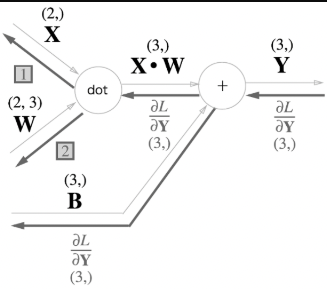
행렬 곱을 수행할 때는, 피연사자간의 형상 (Shape)을 일치시켜야 한다. 아래 이미지를 보면, 의 Shape은 (2,) 이며, 의 Shape은 (2,3)으로, 열(Column)과 행(Row)의 원소가 서로 일치한다.
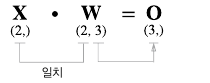
Numpy를 통해, 행열의 Shape에 대한 규칙을 자세히 알아보자.
-
numpy 행렬 정의 for X, W, B.
import numpy as np X = np.random.rand(2) W = np.random.rand(2,3) B = np.random.rand(3) -
를 출력했을 때, Row = 1 Column = 2, Shape = (2,)가 되는 것을 알 수 있다.
print(X) print(X.shape)[0.057618 0.04088931] (2,) -
를 출력했을 때, Row=2, Column=3, Shape = (2,3)이 나온다. 서로간의 차원(Dimension)이 불일치 하기에 행렬 곱을 수행할 수 없다는 에러가 출력되었다.
print(W) print(W.shape)[[0.07086644 0.71153285 0.0462262 ] [0.35796734 0.58845011 0.47938425]] (2, 3) -
와 의 행렬 곱을 수행할 때, Shape을 일치시키는 경우와 일치시키지 않는 경우이다.
print(X.dot(W)) # (2,) * (2,3) = (1,3) print(X.dot(W).shape)[0.25628222 0.68173574 0.66850759] (3,)print(W.dot(X)) # (2,3) * (2,) = Shape Error--------------------------------------------------------------------------- ValueError Traceback (most recent call last) <ipython-input-7-80d107281bb5> in <module>() ----> 1 print(W.dot(X)) ValueError: shapes (2,3) and (2,) not aligned: 3 (dim 1) != 2 (dim 0)
Affine 계층의 역전파
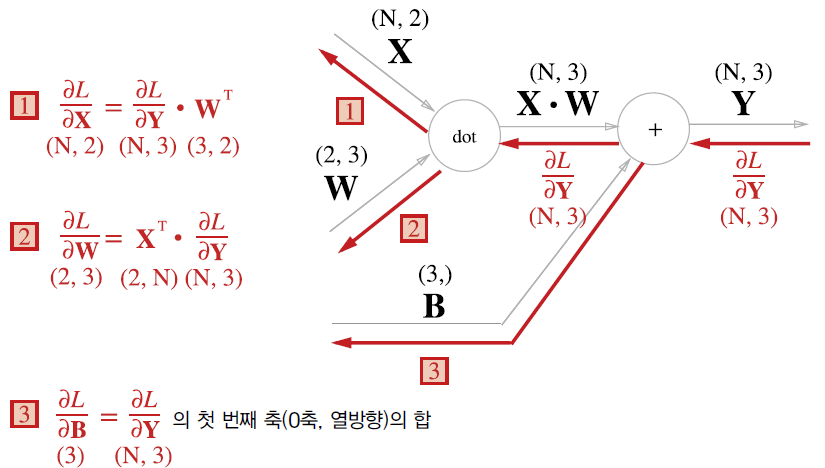
Affine 계층에서 행렬 곱에 대한 역전파는, 순전파시 입력 신호를 서로 Switch하여 곱한다 (순전파 입력신호의 Shape과 일치시키기위해, X와 W의 위치와 전치행렬을 사용한다.)
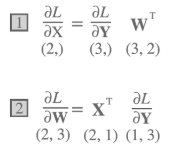
입력신호를 N개의 Batch로 전달할 때는, 차원의 형상이 (N, #)으로만 변형된다.
Affine 계층 구현하기
Affine 계층을 클래스로 구현할 때,
# Affine 계층 구현 하기
class Affine:
def __init__(self, W, b): # 가중치와 바이어스
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x): #
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T) # Shape을 고려하여, 역전파의 이전 입력신호 dout과 W의 전치행렬을 내적한다.
self.dW = np.dot(self.x.T, dout) # Shape을 고려하여, x의 전치행렬과 역전파의 이전 입력신호 dout을 내적한다.
self.db = np.sum(dout, axis = 0) # Bias는 역전파의 입력신호를, 순전파의 입력신호의 형상과 일치시키기위해 Sum을 통해 원소수를 일치시킨다.
return dx Softmax-with-Loss 계층
아래는 모델이, 전달된 다범주 입력 신호를 어떻게 정답을 찾는지 보여주는 그래프이다.
입력 신호는 (이미지) Affine / ReLu 계층을 거쳐 Score를 추론하고, Score는 Softmax 함수를 통해 정규화 되어 확률값으로 반환한다.
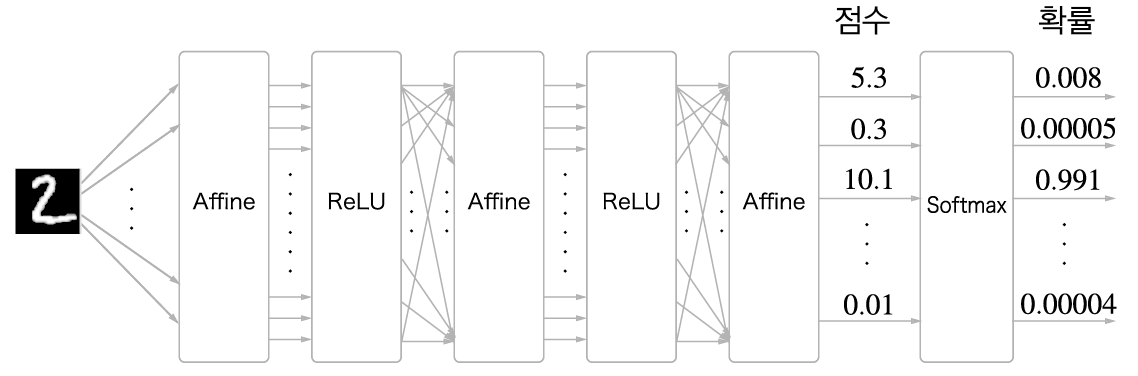
그리고 추론한 확률 분포와 정답 분포를 비교하기위해 손실함수 계층을 추가한다. 아래는 Softmax함수와 Cross Entropy 손실함수의 계층을 구현한 과정을 표현한다.
- t: 정답 분포
- y: Softmax 함수를 거친 확률 분포
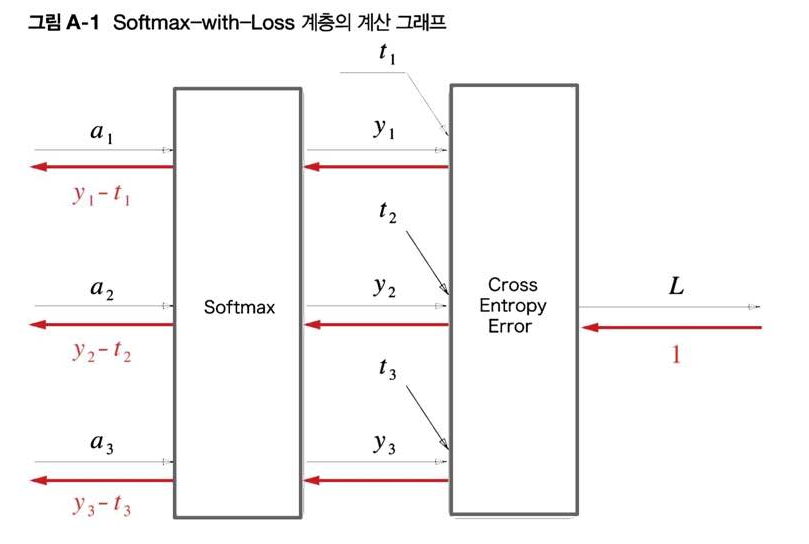
Loss 계층에서 발생한 오차는 앞 계층에 역전파를 통해 기울기 값을 구하여 가중치와 편향을 업데이트 (학습)하는 과정을 거치게 된다.
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 손실
self.y = None # y: Softmax 결과
self.t = None # t: 정답 레이블
def forward(self, x, t): # 입력 x와 정답레이블 t를 인자로 받는다.
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size
return dx swl = SoftmaxWithLoss()
a = np.array([1,8,3])
t = np.array([0,1,0])
print(swl.forward(a,t))
print(swl.backward())0.007620616629495912
[ 0.00030165 -0.00253058 0.00222893]여기 까지가, 입력 신호의 순전파와 역전파의 과정이다. 다음 포스팅에서는, Two Affine Layer를 구현하고 역전파를 통해 가중치와 매개변수를 업데이트하는 코드를 살펴보자.
