신경망의 구조
신경망은 다음과 같이, 입력층, 은닉층, 출력층으로 나눌 수 있다.
입력층에서 출력층까지 순방향(foward)으로 신호가 전달되는 구조이다.
최종적으로, 가중치 w를 학습하고 최적화된 w를 찾는것이 목적이다.
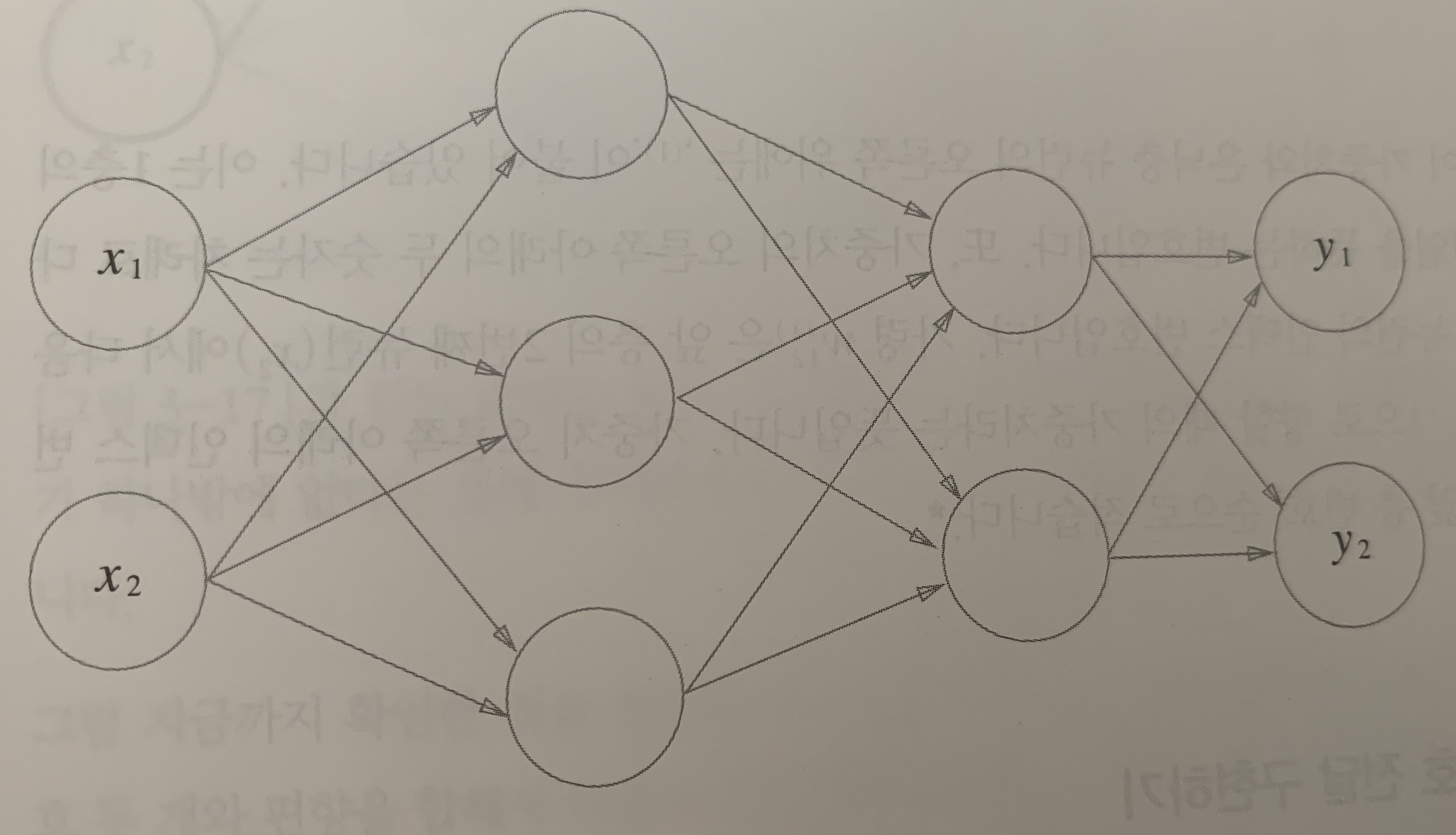
아래는, 입력층 은닉층 출력층 까지 신호전달이 어떻게 진행되는지 확인하고, 이를 간단히 구현하자.
1층: 입력층에서 은닉층(1)으로 !
편향(bias)가 포함된, 3층 신경망 구조이다.
-
입력신호 , 는 첫번째 은닉층의 뉴런으로 각각 전달된다. 이때 각 신호는 가중치 와 가중합 한다.
- = + +
- = + +
- = + +
참고: 의 인덱스는, 다음 뉴런(a) 이전 뉴런(x).
-
각 뉴런의 가중합된 는 활성화 함수 를 거쳐 출력 을 결정한다.
1층 코드 구현
활성화 함수중 하나로 Sigmoid 함수를 사용하여 구현한다.
import numpy as np
def sigmoid(x):
return 1 / (1+ np.exp(-x))
X = np.array([1.0,0.5]) # 입력층 신호
W1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]]) # 1층 가중치
B1 = np.array([0.1,0.2,0.3]) # 1층 편향
print(X.shape)
print(W1.shape)
print(B1.shape)
A1 = np.dot(X,W1) + B1 # 가중합
print(A1)
Z1 = sigmoid(A1) # 활성화 함수
print(Z1)(2,)
(2, 3)
(3,)
[0.3 0.7 1.1]
[0.57444252 0.66818777 0.75026011]2층: 은닉층(1)에서 은닉층(2)로 !
1층과 동일하지만, 입력신호가 활성화 함수를 거친 이라는 점만 차이가 있다.

2층 코드 구현
W2 = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]]) # 2층 가중치
B2 = np.array([0.1,0.2]) # 2층 편향
A2 = np.dot(Z1,W2) + B2 # 2층 가중합
print(A2)
Z2 = sigmoid(A2) # 활성화 함수
print(Z2)[0.51615984 1.21402696]
[0.62624937 0.7710107 ]3층: 출력층
은닉층을 거친 신호들을 3층의 출력으로 보낸다. 과정은 동일하지만, 활성화 함수에서 차이가 있다. (출력층의 함수는, 해결하고자 하는 문제에 따라 선택한다.)

코드구현
출력층의 활성화 함수는 sigmoid가 아닌, 항등함수를 써서 그대로 출력으로 내보냈다.
def identity_func(X):
return X
W3 = np.array([[0.1,0.3],[0.2,0.4]]) # 3층 가중치
B3 = np.array([0.1,0.2]) # 3층 편향
A3 = np.dot(Z2,W3) + B3 # 2층의 신호를 3층 가중치와 가중합
Y = identity_func(A3) # 출력
print(Y)전체코드 구현
간단한 3층 신경망 구조를, 코드 구현했을때 다음과 같다.
def init_network():
network = {}
network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
network['b1'] = np.array([0.1,0.2,0.3]) # 1층 편향
network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]]) # 2층 가중치
network['b2'] = np.array([0.1,0.2]) # 2층 편향
network['W3'] = np.array([[0.1,0.3],[0.2,0.4]]) # 3층 가중치
network['b3'] = np.array([0.1,0.2]) # 3층 편향
return network
def foward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x,W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1,W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2,W3) + b3
y = identity_func(a3)
return y
network = init_network() # 가중치 / 편향 정의
x = np.array([1.0, 0.5]) # 입력 신호
y = foward(network, x) # 순방향 신호 전달
print(y)
[0.31682708 0.69627909]