이진 탐색 트리 (Binary Search Tree)

• 왼쪽 자식노드의 키는 부모 노드의 키보다 작음
• 오른쪽 자식 노드의 키는 부모 노드의 키보다 큼
• 각각의 서브 트리도 이진 탐색 트리를 유지
• 중복된 키를 허용하지 않음

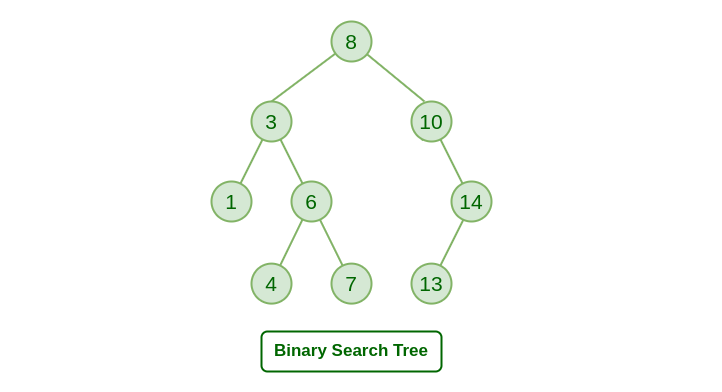
특징

• 데이터가 잘 정렬됨
• 이진트리에 비해 탐색 빠름 (균형 유지가 필요)
  - 균형상태: $O(logn)$
  - 불균형 상태: $O(n)$

구현

탐색

• 찾고자하는 데이터를 루트 노드부터 비교 시작
• 대소 비교를 하여 찾는 데이터가 작으면 왼쪽, 크면 오른쪽 노드로 이동
• 찾는 데이터가 없으면 null 반환
• 어떤 데이터를 찾더라도 최대 트리 높이 만큼의 탐색이 이루어짐

삽입

• Root 부터 비교 시작(중복 키 발견시 노드 추가하지 않고 종료)
• 삽입할 키가 현재 노드의 키보다 작으면 왼쪽으로 이동
• 삽입할 키가 현재 노드의 키보다 크면 오른쪽으로 이동
• Leaf 노드에 도달후 키 비교하여 작으면 왼쪽, 크면 오른쪽에 삽입

public void addNode(int key) {
    if(this.head == null){
        this.head = new Node(key, null, null);
    } else {
        Node cur = this.head;

        while(true){
            Node pre = cur;
            if(key < cur.key){
                cur = cur.left;
                if(cur == null){
                    pre.left = new Node(key, null, null);
                    break;
                }
            } else {
                cur = cur.right;
                if(cur == null){
                    pre.right = new Node(key, null, null);
                    break;
                }
            }
        }
    }
}

삭제

public void removeNode(int key) {
    Node parent = null;
    Node sucessor = null;
    Node predecessor = null;
    Node child = null;

    Node cur = this.head;
    while(cur != null){
        if(key == cur.key){
            break;
        }
        parent = cur;
        if(key < cur.key){
            cur = cur.left;
        } else {
            cur = cur.right;
        }
    }

    if(cur == null){
        System.out.println("key에 해당하는 노드가 없습니다.");
        return;
    }

삭제 대상 노드가 Leaf노드인 경우

• 삭제 대상 노드 삭제
• 부모 노드의 해당 자식 링크 null로 변경

    if(cur.left == null && cur.right == null){ // leaf 노드인 경우
        if(parent == null){
            this.head = null;
        } else{
            if(parent.left == cur){
                parent.left = null;
            } else {
                parent.right = null;
            }
        }
    } 

삭제 대상 노드에 자식 노드가 하나 있는 경우

• 자식 노드를 삭제 대상 노드의 부모노드에 연결
• 삭제 대상 노드 삭제

    else if(cur.left != null && cur.right == null || cur.left == null && cur.right != null){ // 자식 노드가 하나인 경우
        if(cur.left != null){
            child = cur.left;
        } else{
            child = cur.right;
        }
        if(parent == null){
            this.head = child;
        } else {
            if(parent.left == cur){
                parent.left = child;
            } else {
                parent.right = child;
            }
        }

    }

삭제 대상 노드에 자식노드가 둘인 경우

• i 삭제 대상 노드의 왼쪽 서브트리에서 가장 큰 노드 선택
• ii 삭제 대상 노드의 오른쪽 서브트리에서 가장 작은 노드 선택
• i, ii에서 선택한 노드를 삭제대상 노드 위치로 올림
• 위로 올리는 과정에서 다른 자식 노드들의 링크 연결작업 진행
• 삭제 대상 노드 삭제

    else{ // 자식 노드가 둘인 경우
        predecessor = cur;
        sucessor = cur.left;
        while(sucessor.right != null){
            predecessor = sucessor;
            sucessor = sucessor.right;
        }
        predecessor.right = sucessor.left;
        sucessor.left = cur.left;
        sucessor.right = cur.right;
        if(parent == null){
            this.head = sucessor;
        } else{
            if(parent.left == cur){
                parent.left = sucessor;
            } else{
                parent.right = sucessor;
            }
        }
    }
}

재귀함수로 구현

삽입

public Node addNodeRecursive(Node cur, int key) {
    if(cur == null){
        return new Node(key, null, null);
    }
    if( key<cur.key){
        cur.left = addNodeRecursive(cur.left,key);
    } else {
        cur.right = addNodeRecursive(cur.right, key);
    }
    return cur;
}

삭제

public Node removeNodeRecursive(Node cur, int key) {
    if(cur == null){
        return null;
    }
    if(key< cur.key){
        cur.left = removeNodeRecursive(cur.left, key);
    } else if(key> cur.key){
        cur.right = removeNodeRecursive(cur.right, key);
    } else{
        if(cur.left == null){
            return cur.right;
        } else if(cur.right == null){
            return cur.left;
        } else{
            Node predecessor = cur;
            Node succesor = cur.left;
            while(succesor.right != null){
                predecessor = succesor;
                succesor = succesor.right;
            }
            predecessor.right = succesor.left;
            cur.key = succesor.key;
        }
    }
    return cur;
}