[ML] Math Function

1. 다항함수

• $y = 3x^2 + 2$

1) 다항함수 그래프 그려보기

import matplotlib as mpl

plt.figure(figsize=(12,8))
plt.plot(x,y)

# plt.grid()
mpl.style.use('seaborn-whitegrid')

plt.xlabel('$x$', fontsize= 15)
plt.ylabel('$3x^2+2$', fontsize= 15)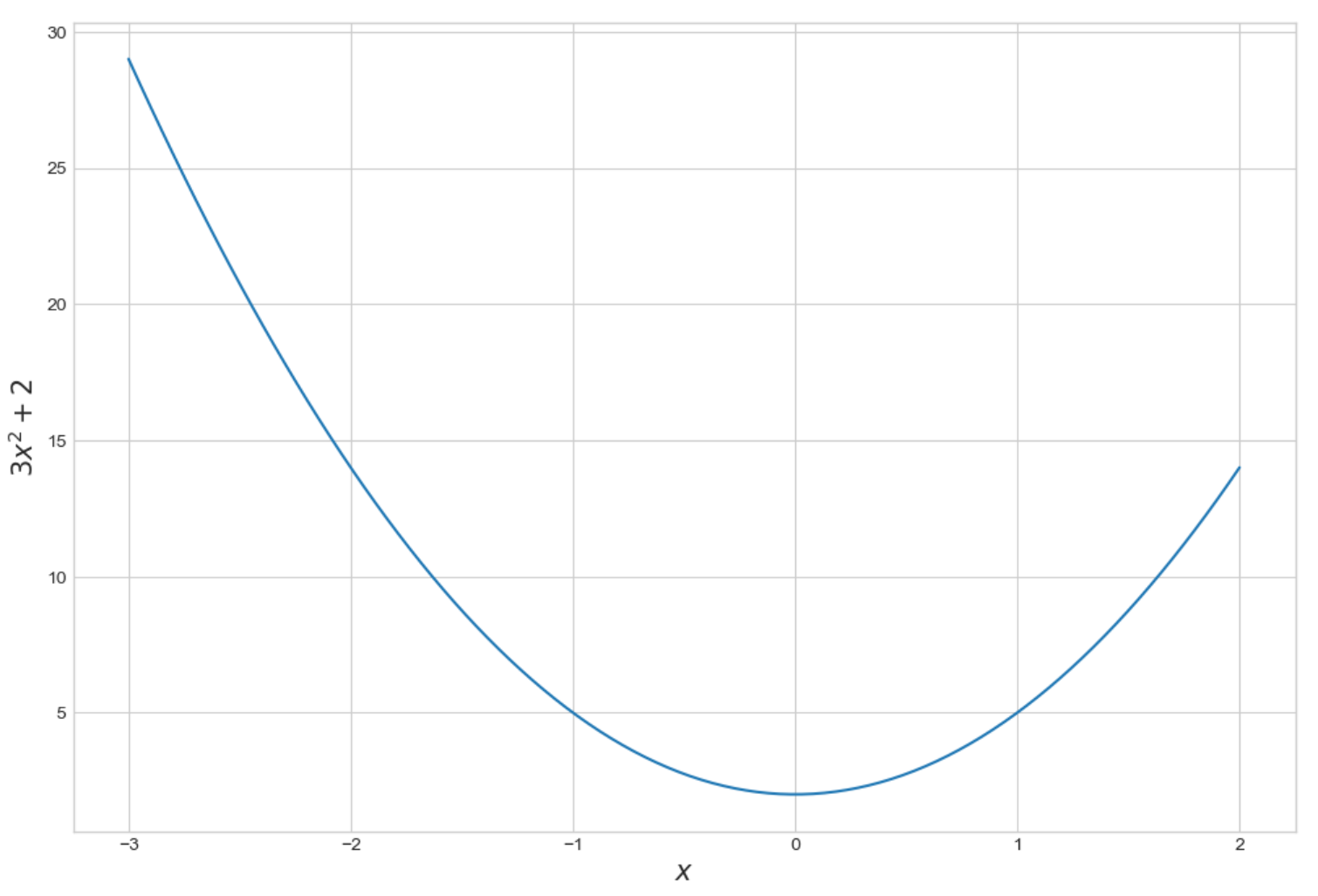

2) 다항함수의 x 축 방향 이동

x = np.linspace(-3, 2, 100)
y1 = 3 * x**2 + 2
y2 = 3 * (x+1)**2 + 2

plt.figure(figsize=(12,8))
plt.plot(x,y1, lw=2, ls='dashed', label = '$3x^2+2$')
plt.plot(x,y2,label = '$3(x+1)^2+2$')
plt.legend(fontsize=15)

# plt.grid()
mpl.style.use('seaborn-whitegrid')

plt.xlabel('$x$', fontsize= 15)
plt.ylabel('$y$', fontsize= 15) 

plt.show()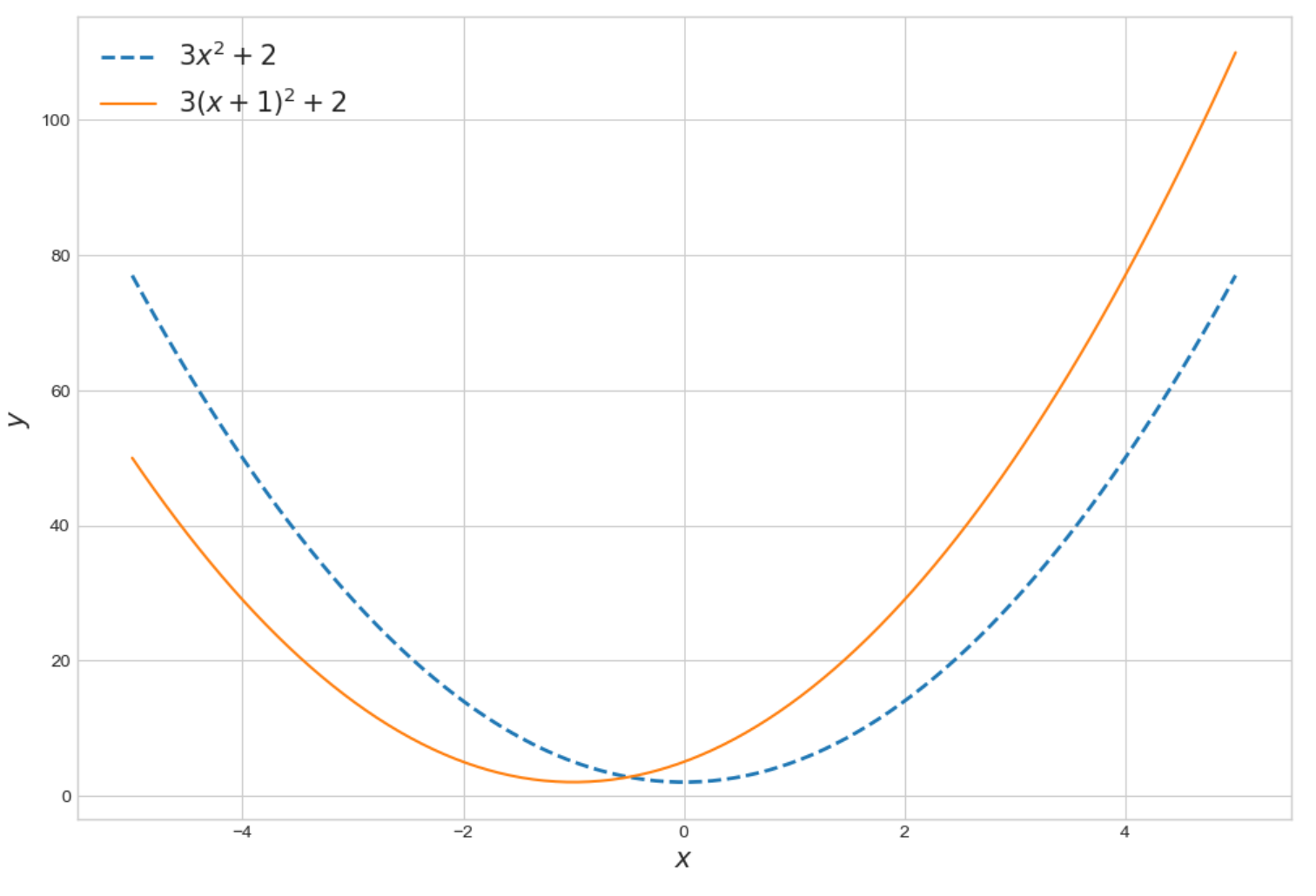

2. 지수 함수

• $f(x) = a^x$

1) 지수함수 그래프 그려보기

x = np.linspace(-2, 2, 100)

a11, a12, a13 = 2,3,4
y11, y12, y13 = a11**x, a12**x, a13**x

a21, a22, a23 = 1/2, 1/3, 1/4
y21, y22, y23 = a21**x, a22**x, a23**x

fig, ax = plt.subplots(1,2, figsize = (12,6))

ax[0].plot(x, y11, color='k', label='$2^x$')
ax[0].plot(x, y12, '--',color='k', label='$3^x$')
ax[0].plot(x, y13, ':',color='k', label='$4^x$')
ax[0].legend(fontsize= 15)

ax[1].plot(x, y21, color='k', label='$(1/2)^x$')
ax[1].plot(x, y22, '--',color='k', label='$(1/3)^x$')
ax[1].plot(x, y23, ':',color='k', label='$(1/4)^x$')
ax[1].legend(fontsize= 15)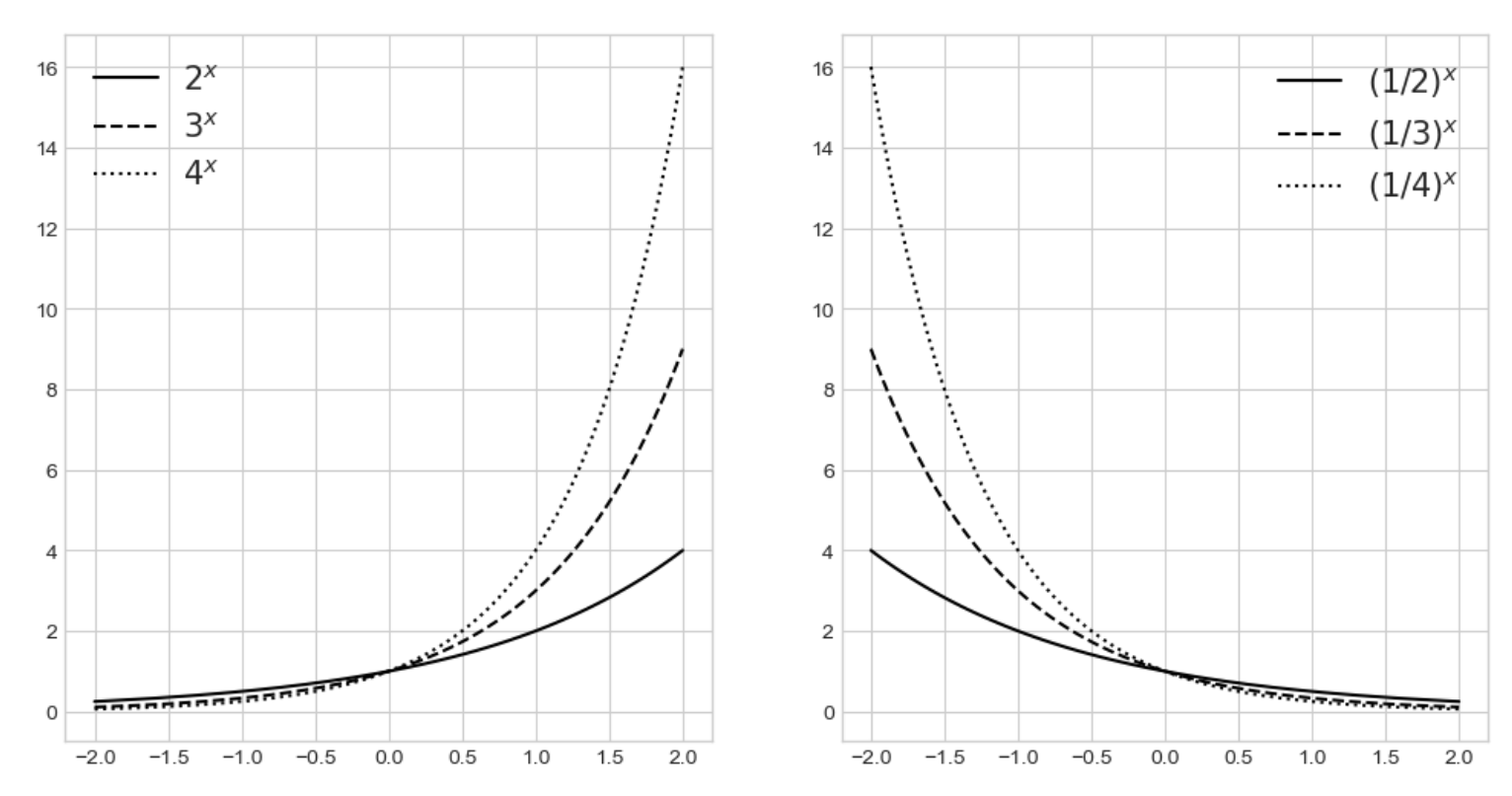

2) 지수 증가

x = np.linspace(1,10)

plt.figure(figsize=(12,6))
plt.plot(x, x**2, '--', color='k', label= '%x^2%')
plt.plot(x, 2**x, color='k', label= '%2^x%')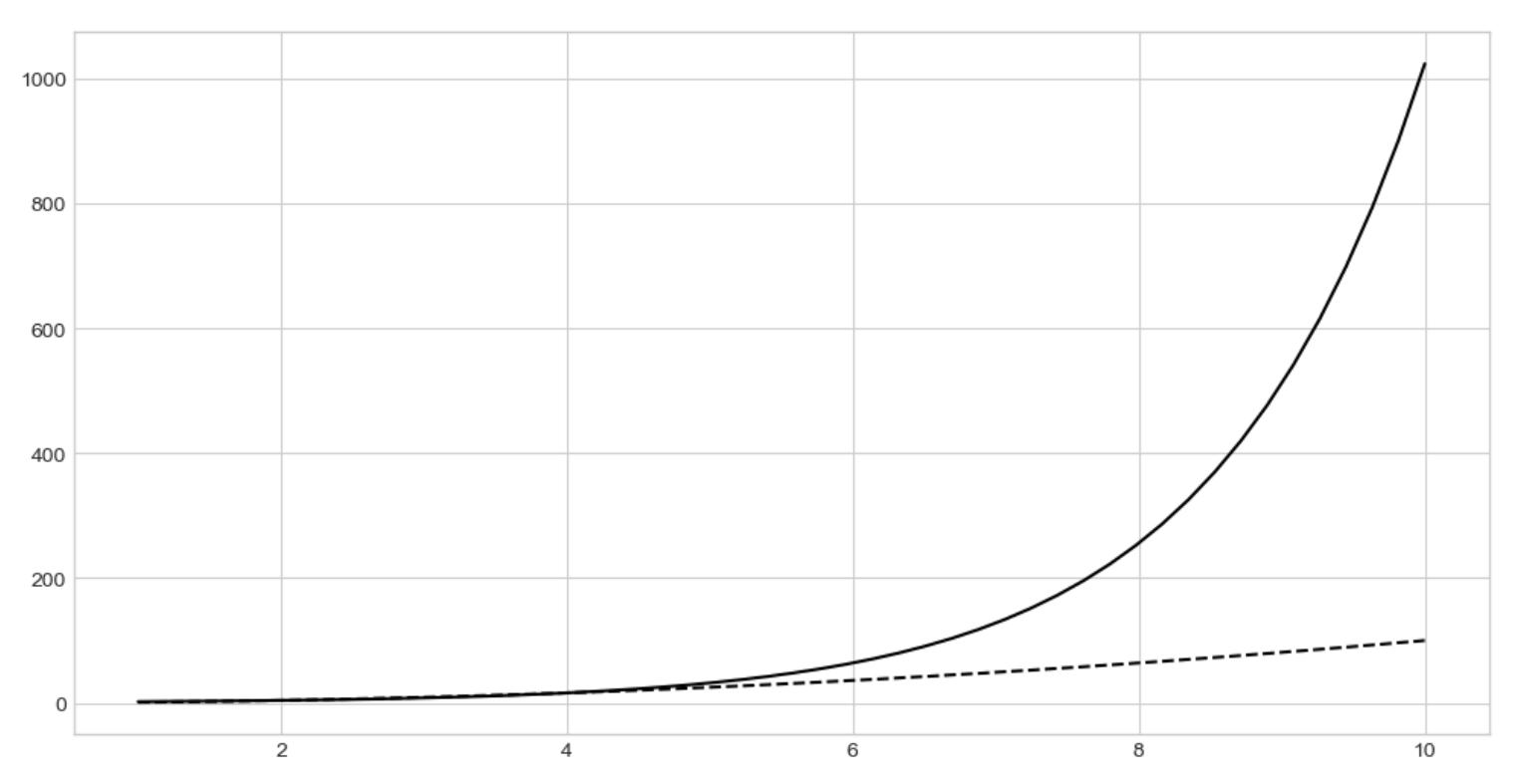

3) 자연상수 $e$

• $(1 + 1/x)^x$

x = np.array([10,100,1000,10000,100000,1000000,10000000])

(1 + 1/x)**x
# array([2.59374246, 2.70481383, 2.71692393, 2.71814593, 2.71826824,
       2.71828047, 2.71828169])

• 어떤 큰 값을 넣어도 2.718281828459045에 수렴
  

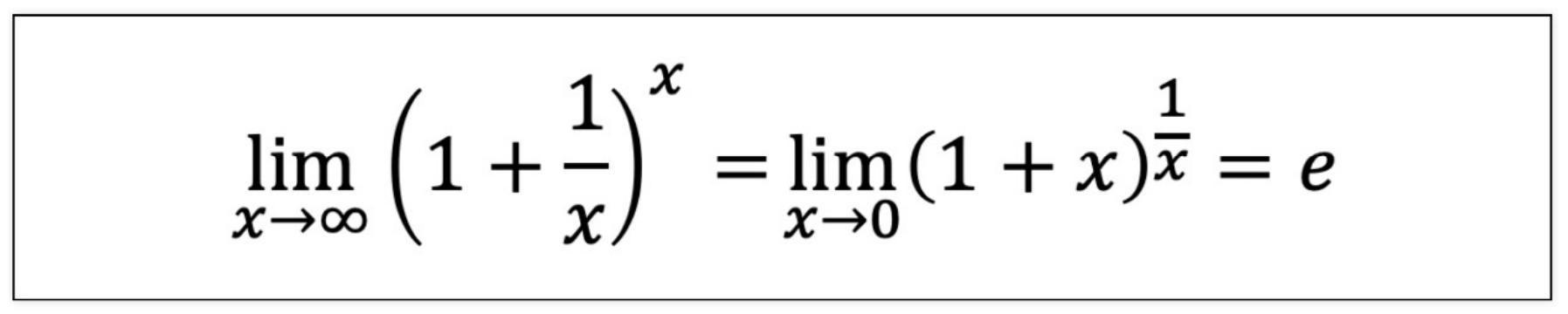
3. 로그함수

• $f(x) = log_ax$

1) 로그함수 법칙

• $2^x = 16$ / $x = log_216$

2) 로그함수 그래프 그려보기

• $log_ax$ = $logx / loga$

def logF(x, base): 
    return np.log(x)/np.log(base)

x1 =  np.linspace(0.0001,5,1000)
x2 =  np.linspace(0.01,5,100)

y11, y12 = logF(x1, 10), logF(x2, np.e)
y21, y22 = logF(x1, 1/10), logF(x2, 1/np.e)

fig , ax = plt.subplots(1,2, figsize=(12,6))

ax[0].plot(x1, y11, label='$\log_{10}x$', color='k')
ax[0].plot(x2, y12, '--',label='$\log_{e}x$', color='k')

ax[0].set_xlabel('$x$', fontsize=15)
ax[0].set_ylabel('$y$', fontsize=15)
ax[0].legend(fontsize=15, loc='lower right')

ax[1].plot(x1, y21, label='$\log_{1/10}x$', color='k')
ax[1].plot(x2, y22,'--', label='$\log_{1/e}x$', color='k')

ax[1].set_xlabel('$x$', fontsize=15)
ax[1].set_ylabel('$y$', fontsize=15)
ax[1].legend(fontsize=15, loc='upper right')

plt.show()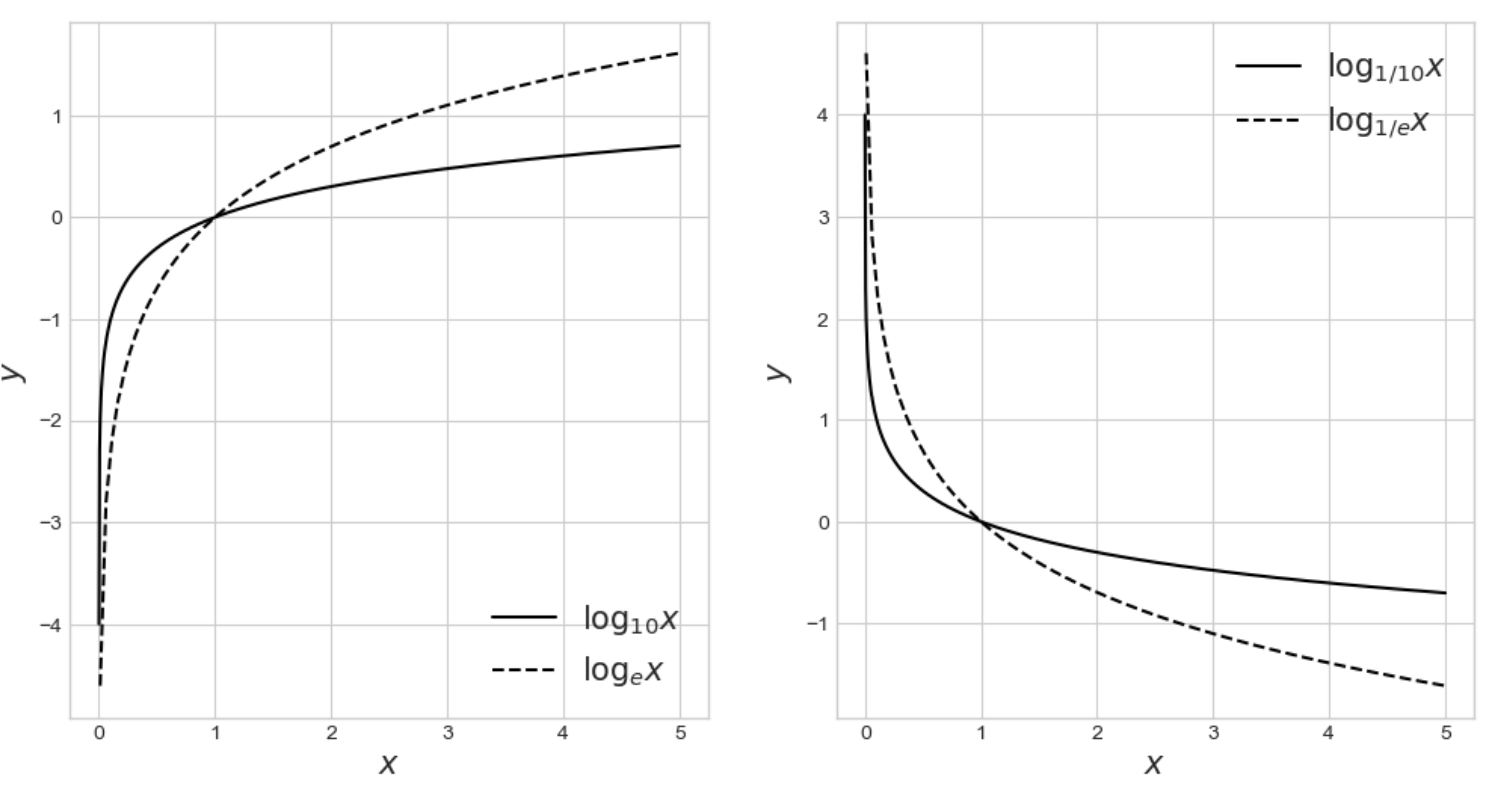

4. 시그모이드 (Sigmoid)

• 1에 수렴, 0의 수렴(0과 1사이의 값을가진다)
  

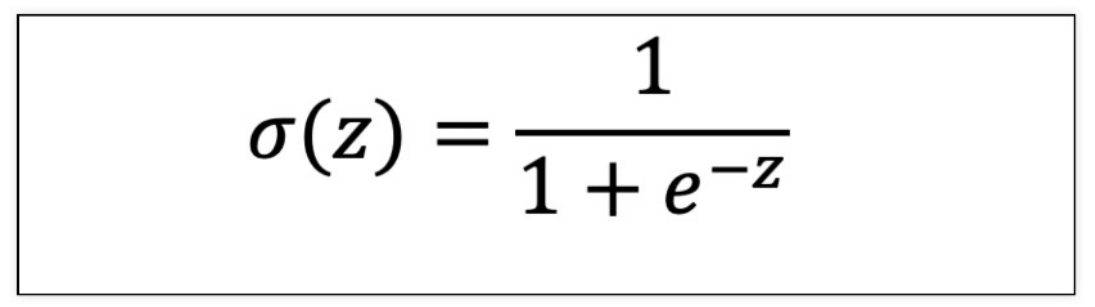
1) 시그모이드 그래프 그려보기

z = np.linspace(-10,10,100)
sigma = 1/(1+np.exp(-z))

plt.figure(figsize=(12,8))
plt.plot(z, sigma)
plt.xlabel('$z$', fontsize= 15)
plt.ylabel('$\sigma(z)$', fontsize= 15) 

plt.show()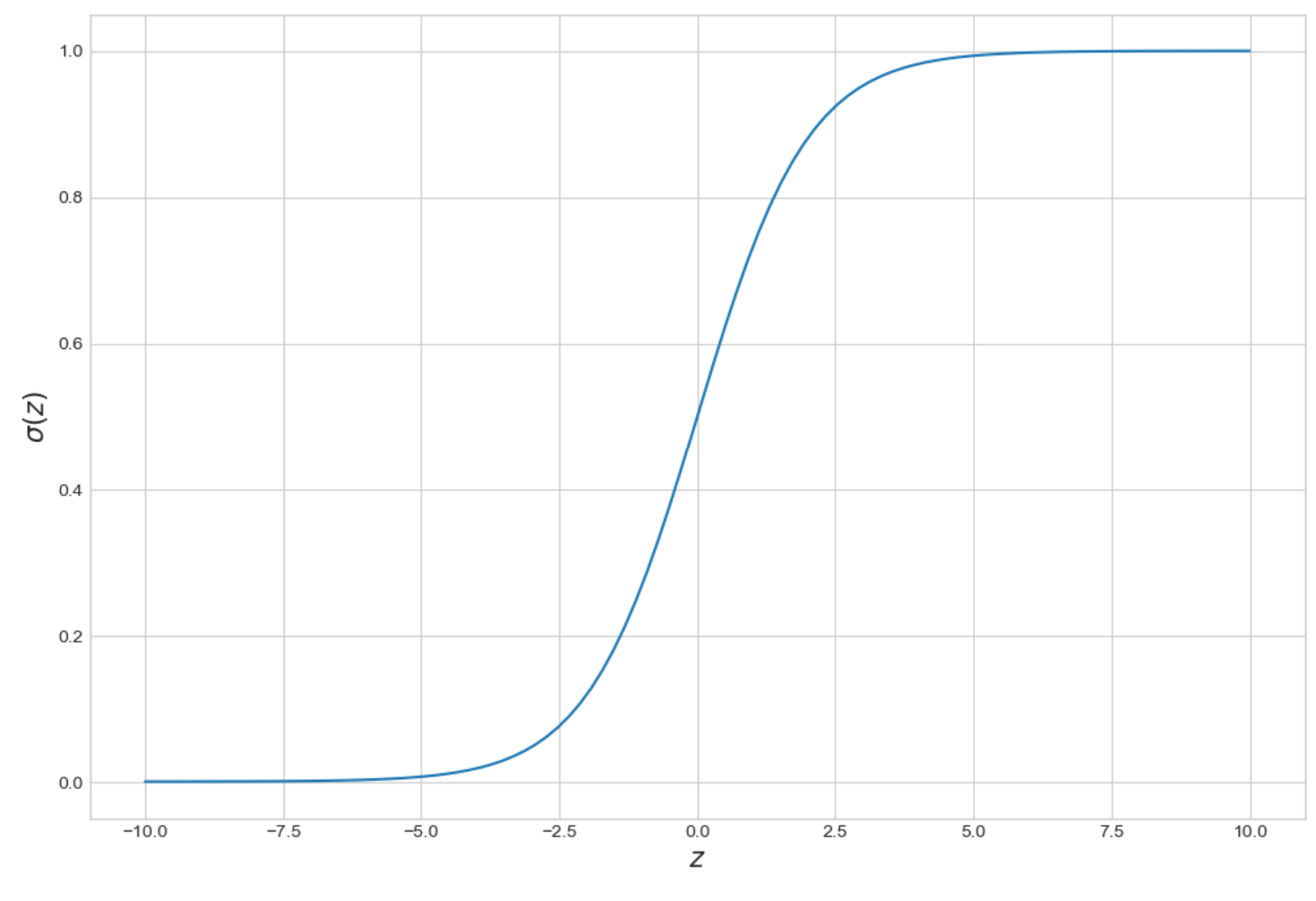

5. 함수의 표현

1) 백터의 표현

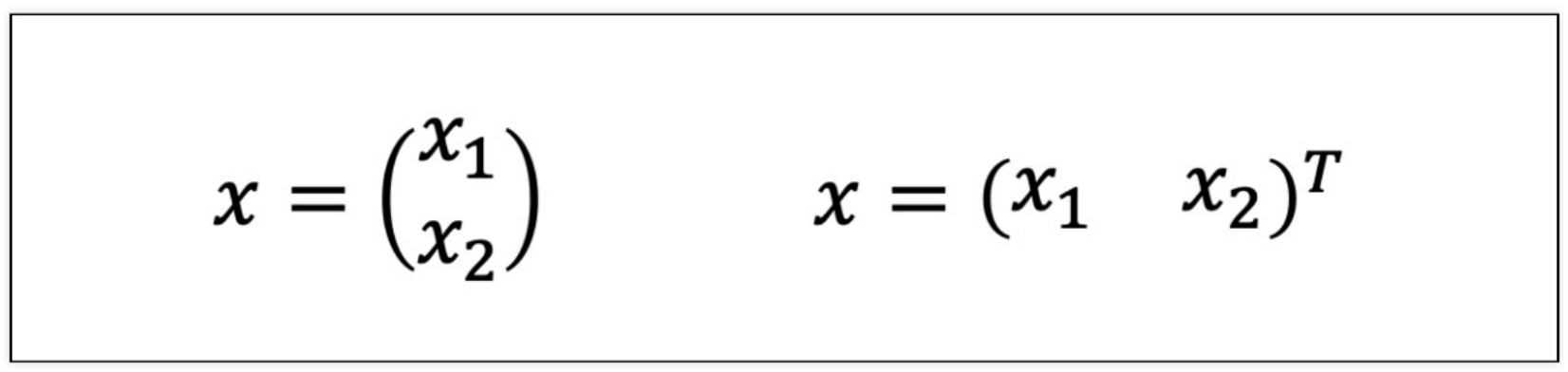
2) 단일 변수 스칼라 함수

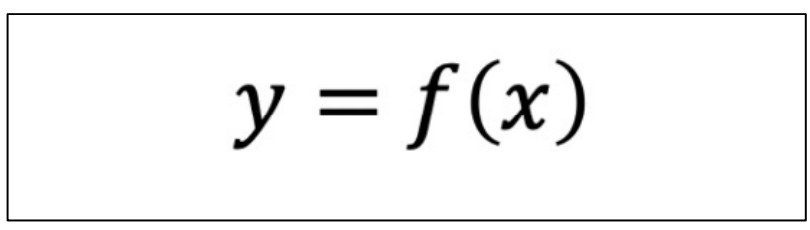
3) 다중 변수 스칼라 함수

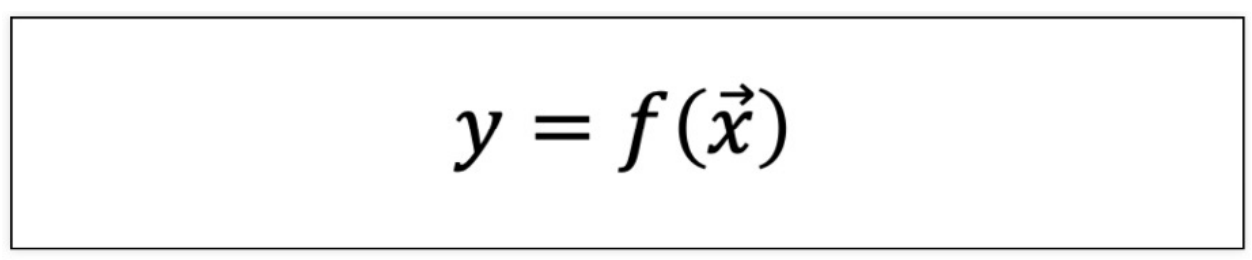
4) 다변수 벡터 함수

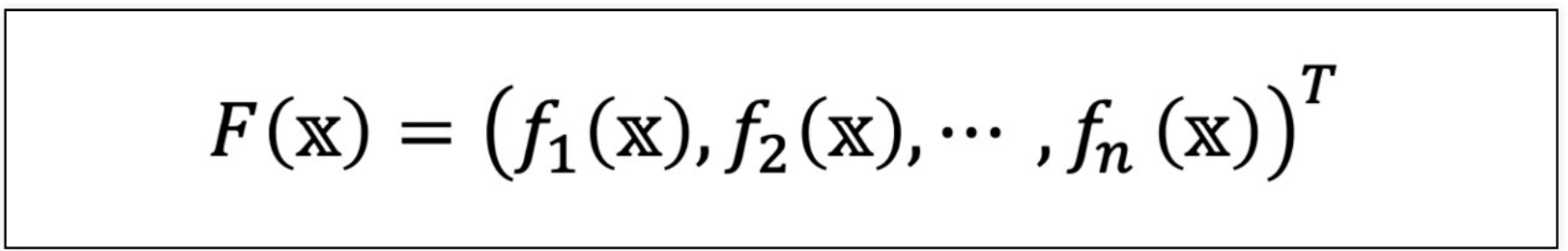
• 다변수 벡터 함수의 예제 그래프 그리기
  

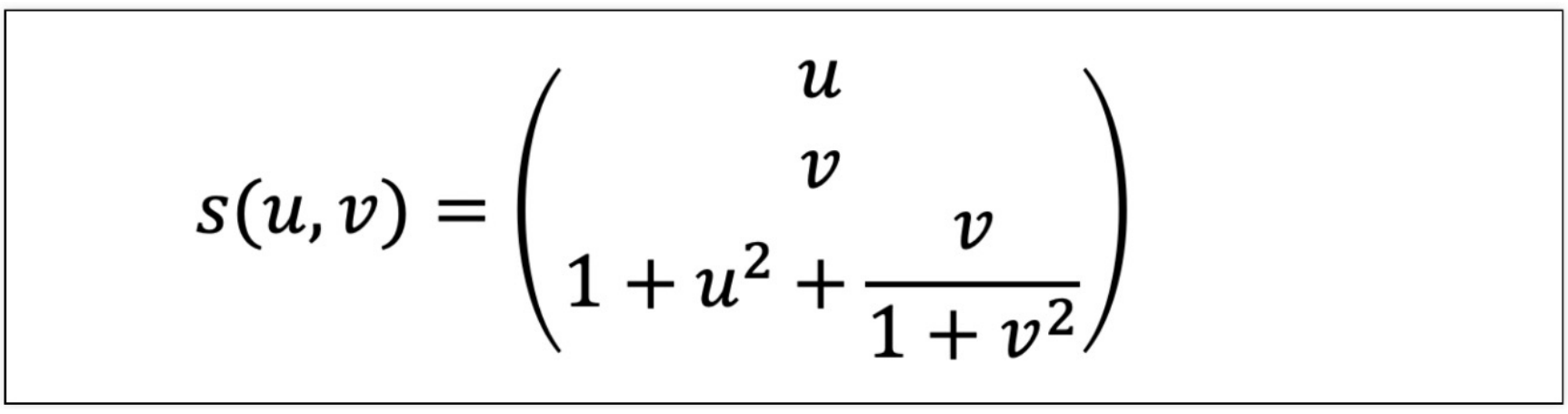
u = np.linspace(0,1,30)
v = np.linspace(0,1,30)

U,V = np.meshgrid(u, v)

X = U
Y = V
Z = (1+U**2) + (V/(1+V**2))

fig = plt.figure(figsize=(7,7))
ax = plt.axes(projection = '3d')

ax.xaxis.set_tick_params(labelsize=15)
ax.yaxis.set_tick_params(labelsize=15)
ax.zaxis.set_tick_params(labelsize=15)

ax.set_xlabel('$x$', fontsize=15)
ax.set_ylabel('$y$', fontsize=15)
ax.set_zlabel('$z$', fontsize=15)

ax.scatter3D(X,Y,Z, marker= '.', color= 'gray')
plt.show()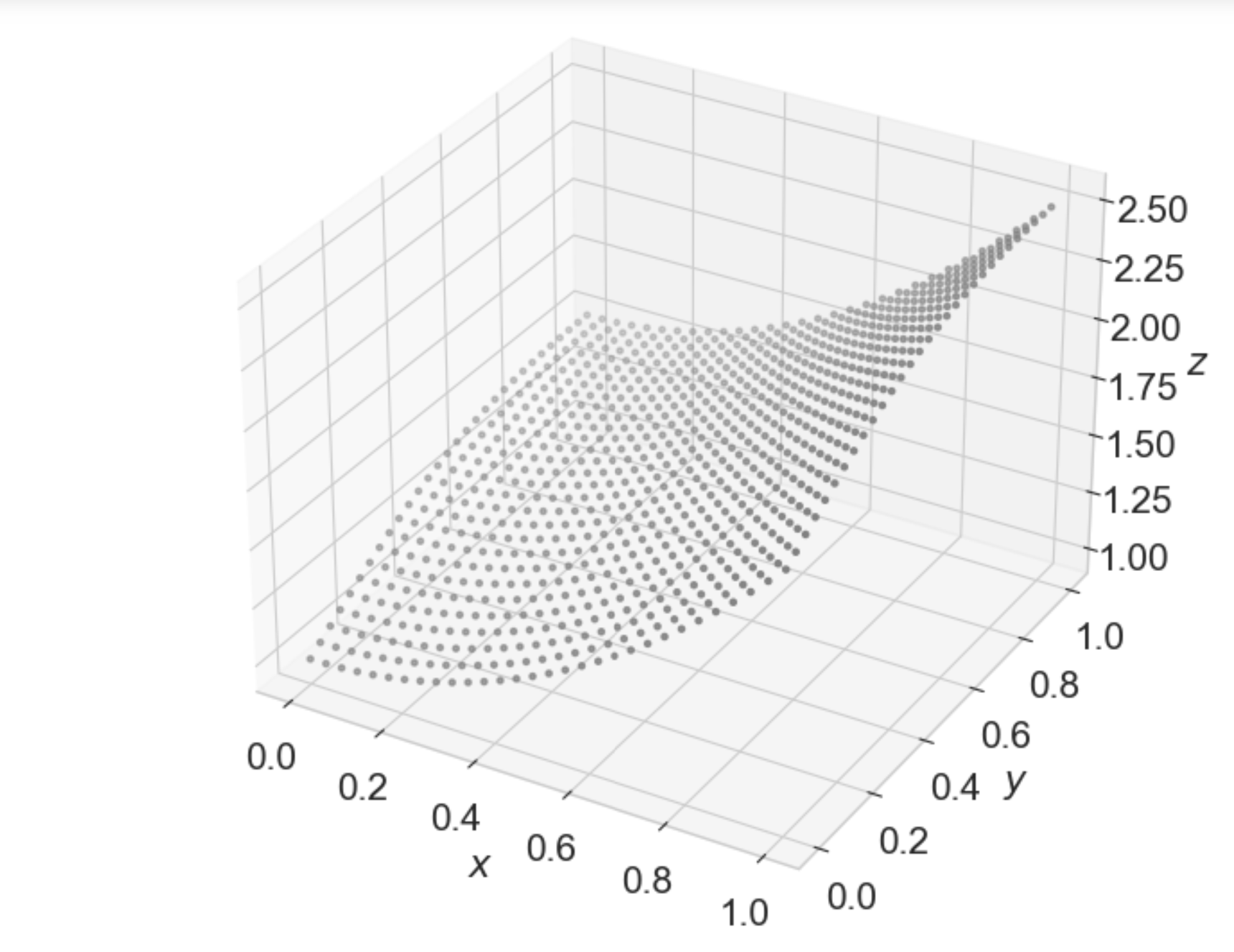

6. 함수합성

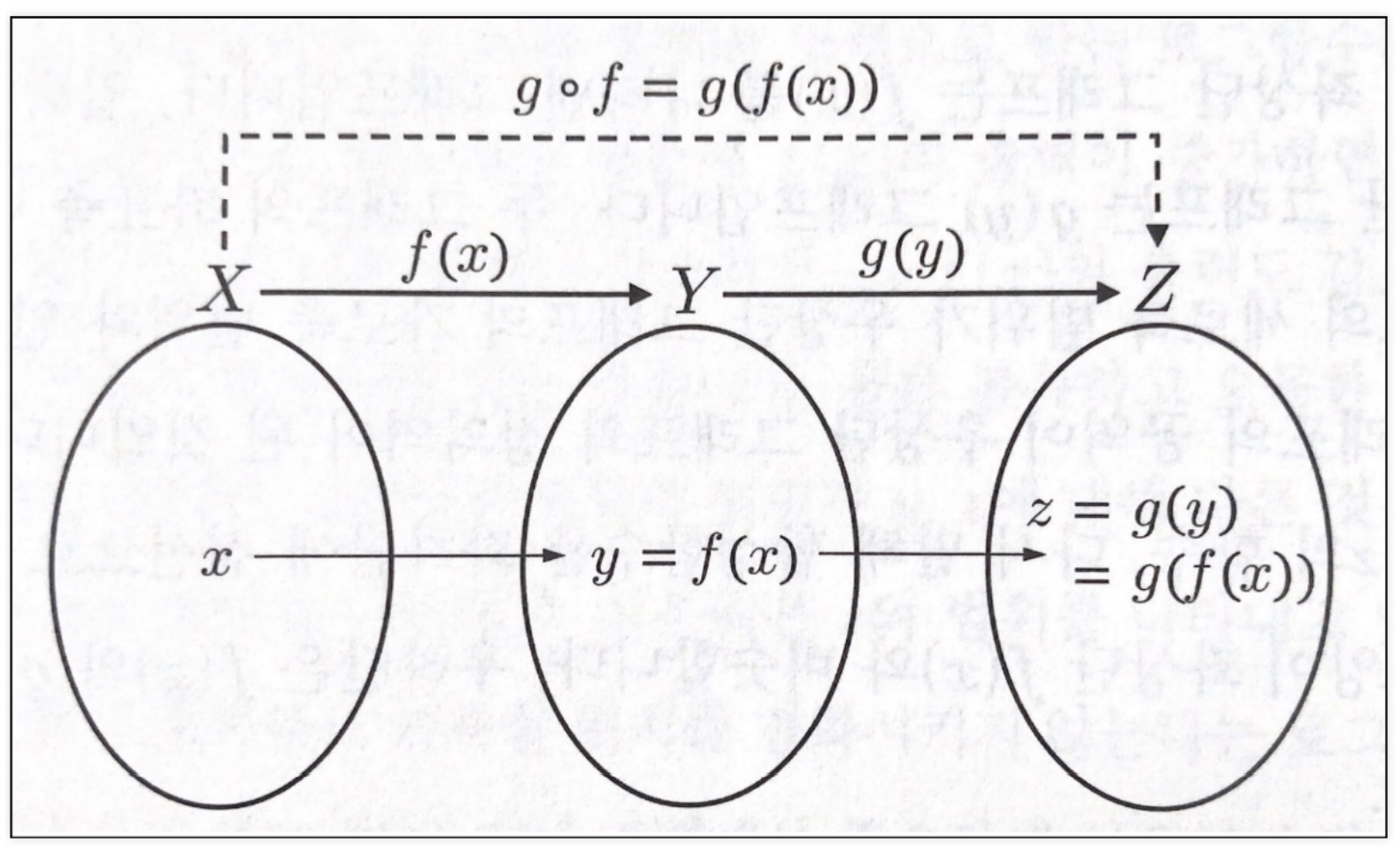
1) 합성을 위한 함수 두개

x = np.linspace(-4,4,100)
y = x**3 - 15*x + 30
z = np.log(y)

fig, ax = plt.subplots(1,2, figsize= (12,6))

ax[0].plot(x,y, label='$x^3 - 15x + 30$', color = 'k')
ax[0].legend(fontsize=15)

ax[1].plot(y,z, label='$\logy$', color = 'k')
ax[1].legend(fontsize=15)

plt.show()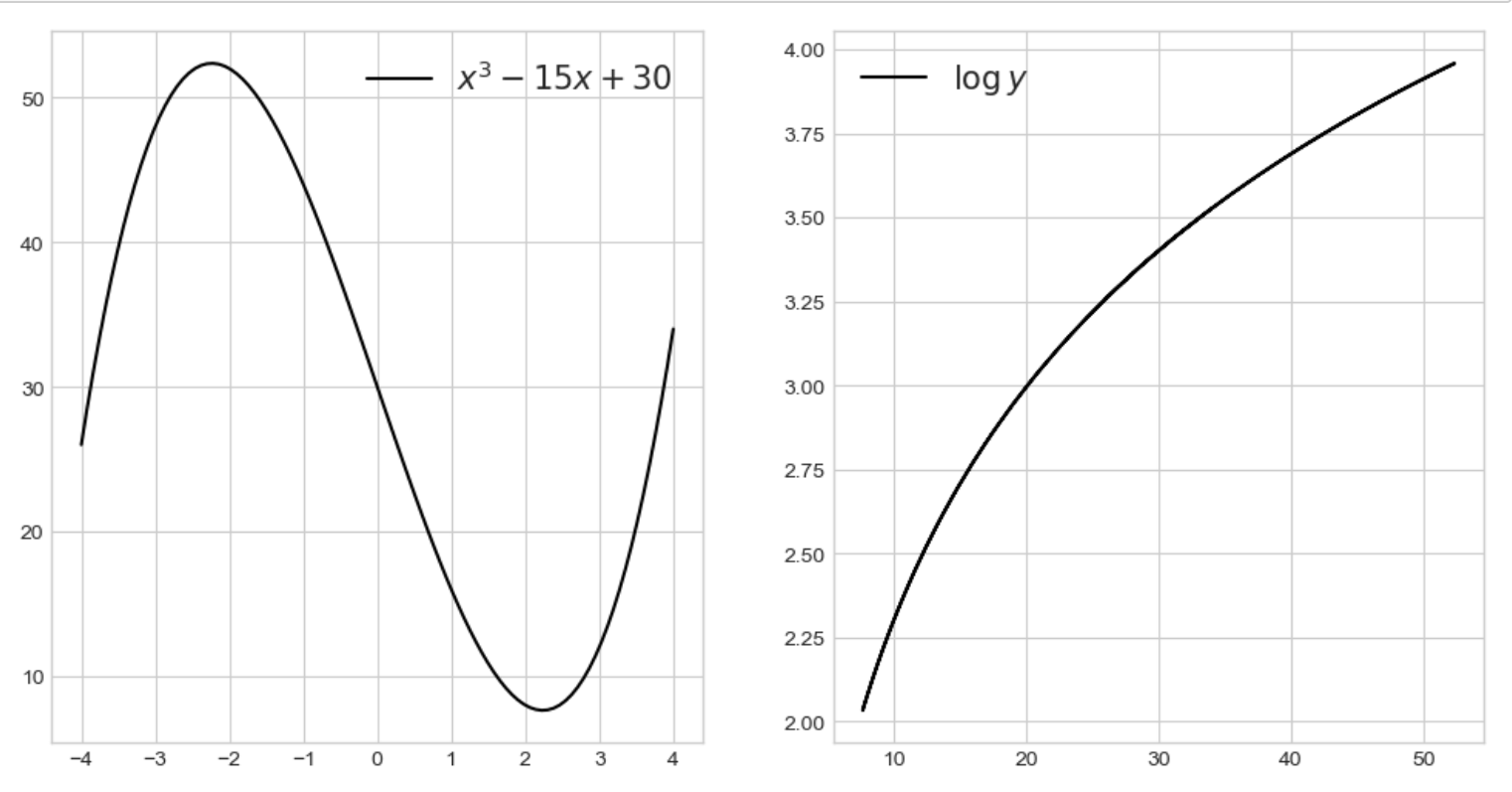

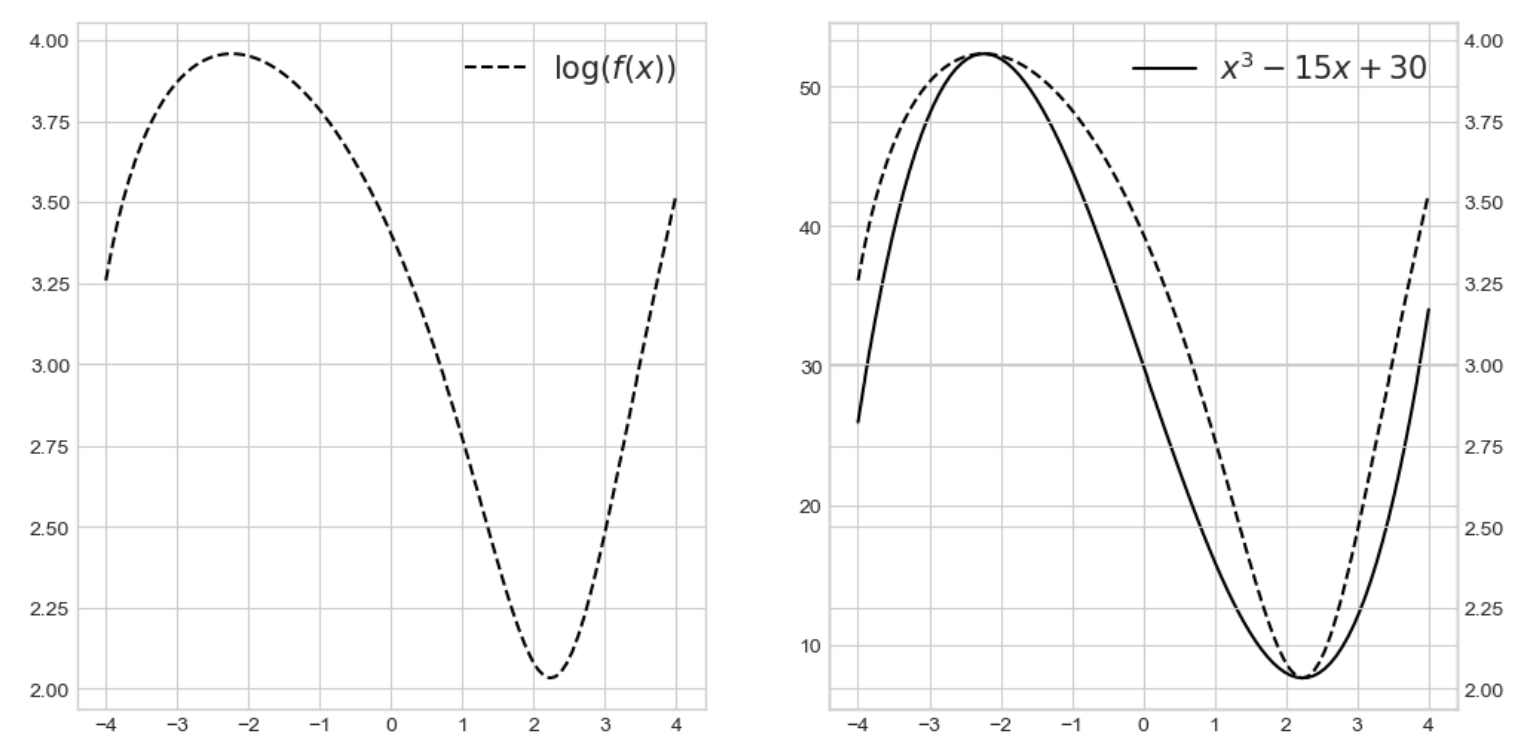
2) 함수 합성 그래프

fig, ax = plt.subplots(1,2, figsize= (12,6))

ax[0].plot(x,z,'--', label='$\log(f(x))$', color = 'k')
ax[0].legend(fontsize=15)

ax[1].plot(x,y, label='$x^3 - 15x + 30$', color = 'k')
ax[1].legend(fontsize=15)

ax_tmp = ax[1].twinx()
ax_tmp.plot(x,z,'--', label=r'$\log(f(x))$', color='k')

plt.show()