시작
머신러닝 개념을 잡기위해 저번 포스팅때는 회귀에 대해 공부해보았다. 이번 포스팅에서는 두번째로 기본이 되는 분류에대해 포스팅 해보겠다.
분류란 ?
분류는 말그대로 특정한 값으로 분류하는것이다. 예시로 특정 요인에 따라 어떤 행동을 했는지 / 안했는지를 분류하는 상황등이 있고 분류값이 2개면 2진분류 , 분류가 여러개이면 다중분류라고 한다.
Logistic Regression (로지스틱 회귀)
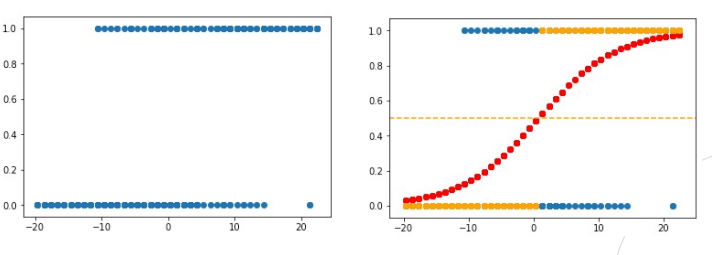
이진 분류를 하는경우 대표적으로 로지스틱 회귀가 있다. 출력값은 시그모이드 함수를 통과시켜지고 0과 1 사이의 값을 갖도록 만들어 이진 분류에 적합하게 조정된다. 로지스틱 회귀는 새로운 입력에 대한 예측을 수행하는데, 예측 확률이 0.5보다 크면 한 클래스로, 그렇지 않으면 다른 클래스로 예측하게된다.
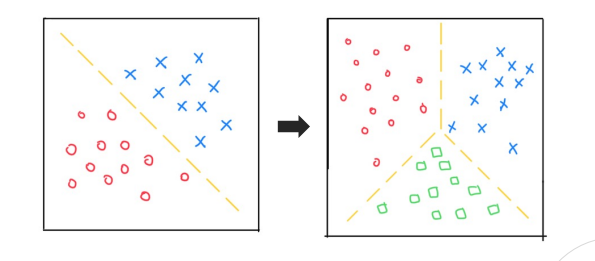
다중 분류
다중 분류인 경우는 소프트맥스 함수를 통해 입력값을 각 클래스에 대한 확률 값으로 변환한다.
우도 확률
-
모델 파라미터 값을 잘 모르지만 안다고 가정했을 경우, 주어진 데이터의 분포
-
우도 확률은 모델의 파라미터 (w)에 대한 함수로 데이터의 분포를 표현
최대 우도 추정법 (Maximum Likelihood Estimation, MLE)
- 현재의 데이터 분포가 나올 확률이 가장 높은 파라미터 == 우도 확률을 최대로 만드는 파라미터
시그모이드 , 소프트 맥스 설명

로지스틱 회귀 , 다중분류 사진
SVM
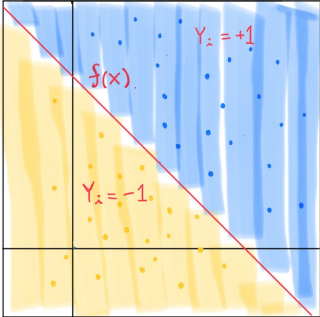
- SVM은 주어진 데이터로 두 클래스 간의 경계를 찾아내고, 이 경계를 최대화하는 방향으로 학습.
- 예측값이 0보다 크면 yR = 1로, 0보다 작으면 yR = −1로 분류
- 아래 사진은 Hyperplane 예시
SVM vs 로지스틱 회귀(LR)
- 클래스가 거의 분리가능(separable)하면, SVM > LR / 아닐 경우 , SVM == LR
- 확률값을 측정하고 싶으면, LR을 사용
- 비선형 바운더리에서는 SVM이 계산적인 면에서 더 좋음
Tree-based Methods
- 예측을 위해 여러 region으로 세분화 하는 방법론
- 회귀,분류 모두 사용가능
- 분류에서는 대표적으로 Decision Tree
Greedy tree-building
- Greedy 방식은 일정 기준(각 region에 5개 이하의 샘플) 만족 시 멈춤
- Top-down, greedy 방법론 보통 사용
- Over-fitting 이슈 발생 (Bias ↓, Variance ↑)
over-fitting이슈를 해결하기 위해 교차 검증 (cross validation)을 통해 optimal subtree 찾거나 , RSS 값이 일정 threshold 만큼 떨어지지 않으면 tree 성장을 멈춰서 해결
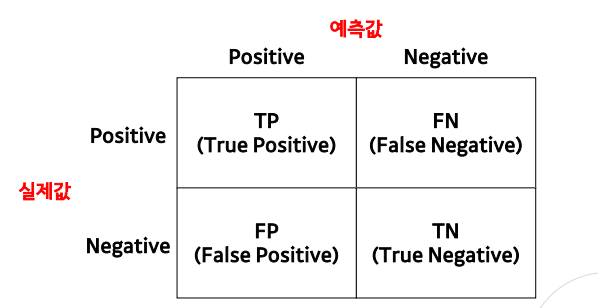
오차 행렬
- 분류모델 성능 측정을 위해 예측값과 실제값을 비교한 표
- 정확도 , 정밀도 , 재현도 , F1 score 도출 가능
평가지표
정확도 (Precision)
- n개의 데이터 샘플 중 예측에 성공한 샘플의 비율
- TP+TN / TP+FN+FP+TN
정밀도 (recall)
- 모델이 Positive로 예측한 것 중 실제값 또한 Positive인 비율
- TP / TP+FP
재현도 (recall)
- 실제값이 Positive인 것 중 모델이 Positive로 예측한 비율
- TP / TP+FN
F1 Score
- 정밀도와 재현도의 조화 평균
- 2 precision recall / precision+recall
후기
머신러닝 분류 관련 강의를 들으면서 깊은 수학적인 내용이 아닌 , 가벼운 이론 위주로 포스팅 해보았다. 메타코드 덕분에 이전에 학습했던 내용들을 오랜만에 정리할 수 있었고 앞으로도 끊임없이 공부해 나갈것이다.
- 메타코드 공식 사이트 : https://mcode.co.kr/
- 강의 유튜브 링크 : https://youtu.be/oyzIT1g1Z3U?feature=shared
#메타코드 #메타코드M #머신러닝 #데이터분석 #분류 #기초 #이론 #데이터
