통계적 가설 검정에서 유의 확률 또는 p-값은 귀무가설이 맞다고 가정할 때 얻은 결과보다 극단적인 결과가 실제로 관측될 확률이다. 실험의 유의확률은 실험의 표본 공간에서 정의되는 확률변수로서, 0~1 사이의 값을 가진다. -위키백과-
우선 위키백과에 따르면 p-value란 위의 의미를 지닌다. 하지만 위의 글을 읽어보면 쉽게 받아들이긴 힘들것이다. 따라서 이것을 조금 더 쉽게 내가 이해한 대로 펼쳐보겠다.
우선 p-value란 귀무가설이 참일 때 극단 적인 값이 나올 확률이다.
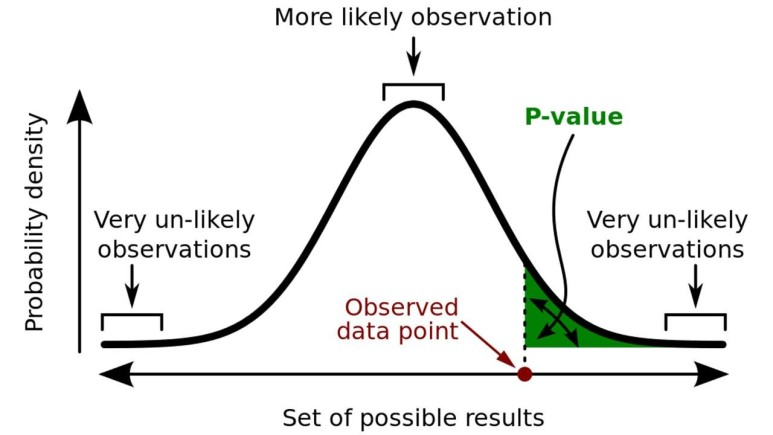
이 말을 이해하려면 일단 귀무가설과 대립가설에 대해 알아야 할것이다. 이전 포스팅에서 정리해 두었지만 다시 한번 간단히 되짚고 넘어가자면, 귀무가설이란 ( 일반적인 것, 평균값과 비슷한 것, 변화가 없는 것) 이라고 할 수 있다. 가령 예를 들어 '사람의 기분은 날씨에 따라 변화가 있을것이다' 라는 가설을 검정하려고 한다.
그렇다면 여기서 귀무가설은 변화가 없다, 일반적이다 가 되어야 하니 '사람의 기분은 날씨에 따라 변화가 없다' 가 될 수 있다.
반대로 대립가설은 연구자가 밝혀내고자 하는 사실이기 때문에, '사람의 기분은 날씨에 따라 변화가 있다' 가 될 것이다.
이를 바탕으로, p-value를 다시 이해해보자면, 귀무가설 즉 변화가 없다라는 주장에서 극단적인 값 즉 날씨에 따른 사람의 기분이 변화가 있는 통계량이 나올 확률을 뜻하게 되는 것이다.
그렇기 때문에, 귀무가설에서는 변화가 없다고 하였지만, 변화가 있다고 나온 통계량이 나올 확률이 일정 % 이하이면 대립가설이 채택 되게 된다.
조금 더 쉽게 풀어 얘기하자면, 귀무가설에서 내가 연구해서 나온 추정치 값(극단적인 값)이 나올 확률(p-value)가 너무 작으므로, 다른 분포에 위치 가능할 것이라고 추론 가능한 것이다.
반대로 p-value가 높에 되면 현재 귀무가설이 참인 분포에서도 p-value(극단적인 값이 나올확률)이 높으니깐 귀무가설이 채택되게 되는 것이다.
따라서 지정된 알파(유의수준)값 보다 p-value가 높으면 귀무가설이 채택되는 것이고, 낮으면 반대로 대립가설이 채택되게 된다.