문제
N개의 수로 이루어진 수열이 주어집니다.
이 수열에서 연속부분수열의 합이 특정숫자 M이하가 되는 경우가 몇 번 있는지 구하는 프로그 램을 작성하세요.
만약 N=5, M=5이고 수열이 다음과 같다면
13123
합이 5이하가 되는 연속부분수열은 {1}, {3}, {1}, {2}, {3}, {1, 3}, {3, 1}, {1, 2}, {2, 3}, {1, 3, 1}로 총 10가지입니다.
[입력설명]
첫째 줄에 N(1≤N≤100,000), M(1≤M≤100,000,000)이 주어진다. 수열의 원소값은 1,000을 넘지 않는 자연수이다.
[출력설명]
첫째 줄에 경우의 수를 출력한다.
입력예제 1
5 5
1 3 1 2 3
출력예제 1
10
문제
예습 이론
- 부분수열의 갯수: rt-lt+1
코드
투포인터를 활용한 문제이다. lt=0, rt=0으로 시작하여 lt는 고정되어있고 rt가 움직인다. arr[rt]를 계속 누적한다. 만약, 누적값이 m보다 더 커진다면, lt의 값을 빼주고 인덱스의 위치를 옮긴다(lt++). 이후, 부분수열의 갯수를 answer에 누적한다.
<html>
<head>
<meta charset="UTF-8">
<title>출력결과</title>
</head>
<body>
<script>
function solution(m, arr){
let answer=0, sum=0, lt=0;
for(let rt=0; rt<arr.length; rt++){
sum+=arr[rt];
while(sum>m){
sum-=arr[lt++];
}
answer+=(rt-lt+1); //부분수열 갯수
}
return answer;
}
let a=[1, 3, 1, 2, 3];
console.log(solution(5, a));
</script>
</body>
</html>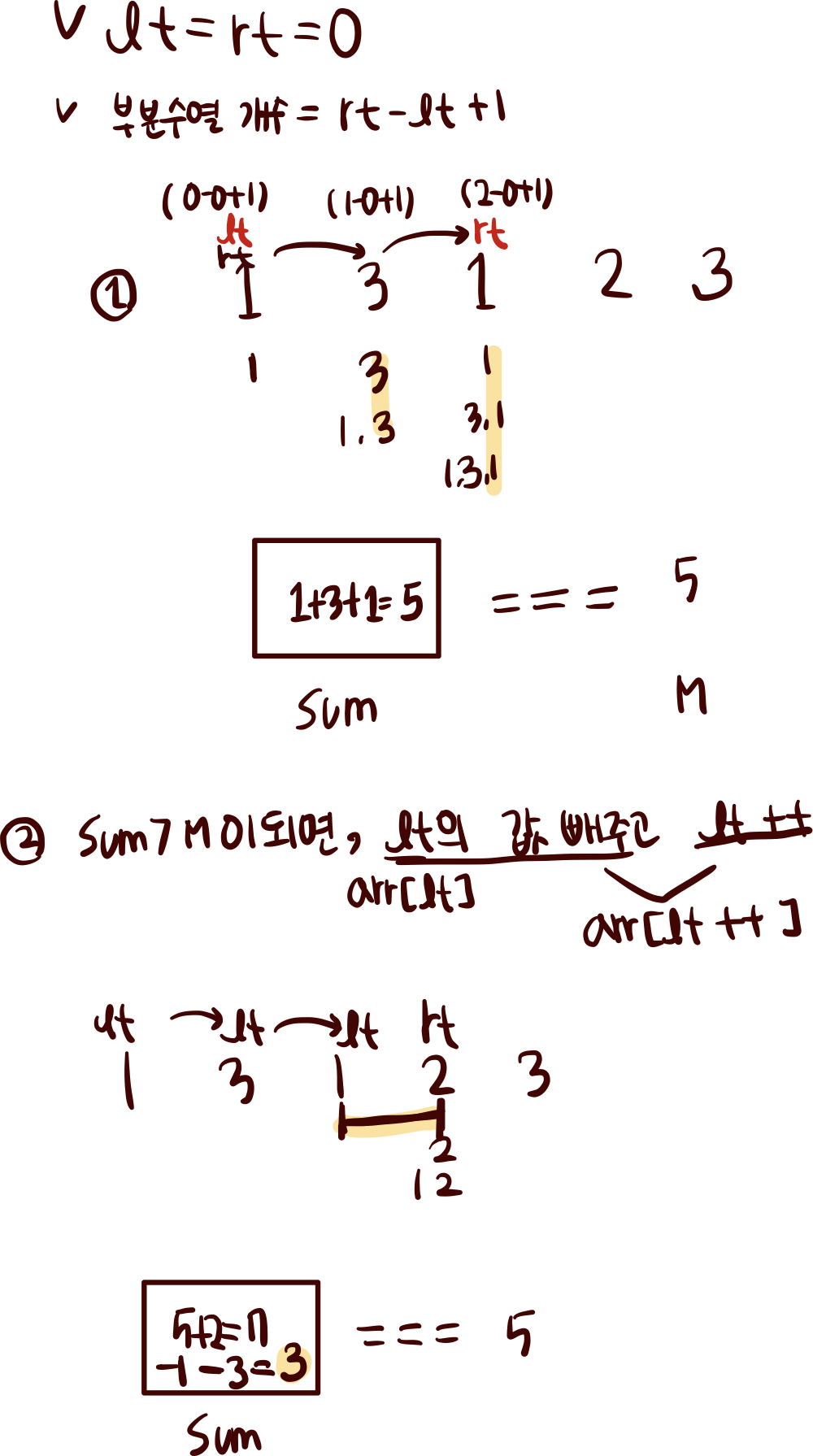
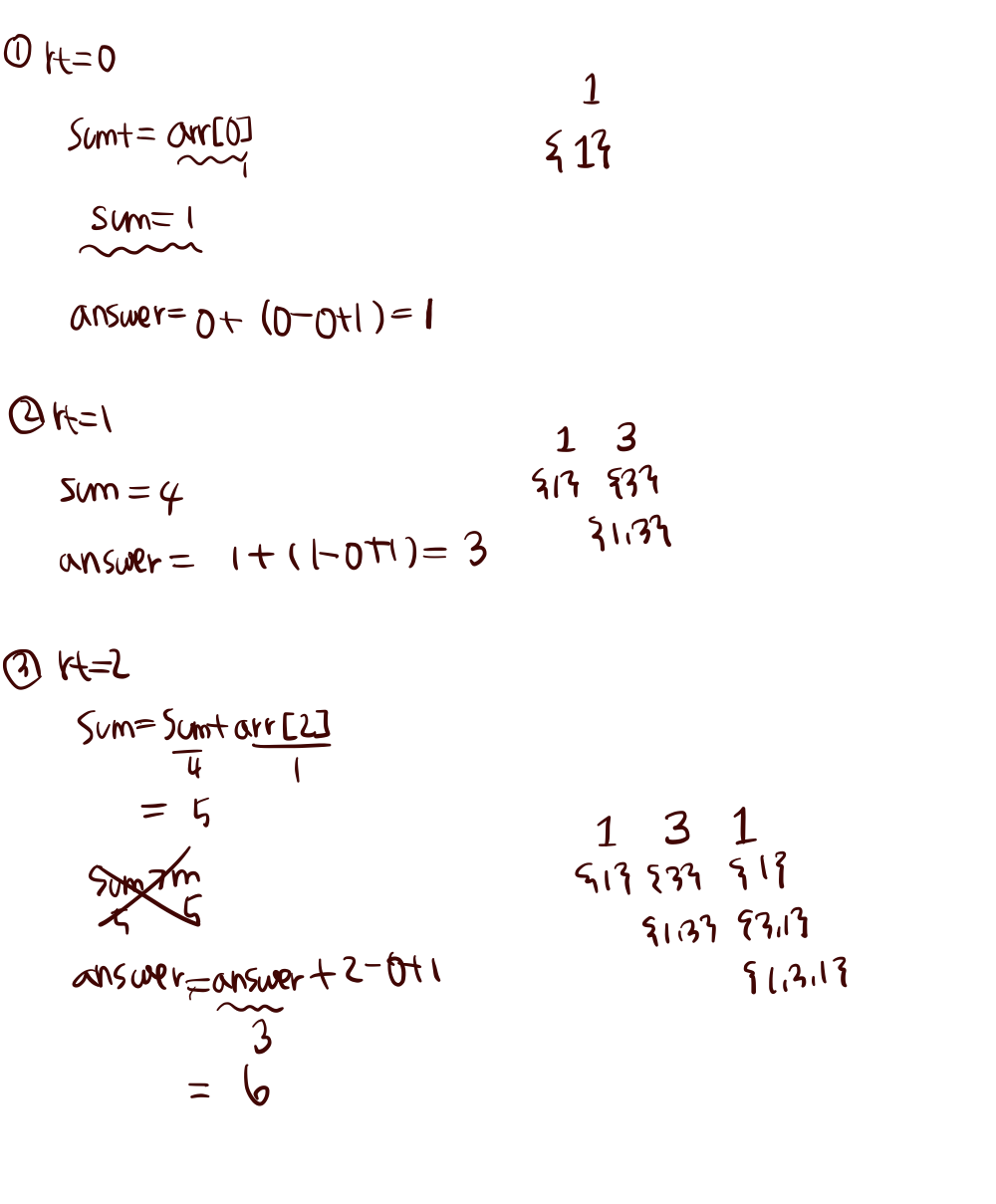

9/12
부분수열의 갯수: rt-lt+1