이 문제는 순열(8-10), 조합의 경우수(8-12)의 응용문제이다. 이해가 안되면 해당 챕터를 다시보고오자!
문제
가장 윗줄에 1부터 N까지의 숫자가 한 개씩 적혀 있다. 그리고 둘째 줄부터 차례대로 파스칼 의 삼각형처럼 위의 두개를 더한 값이 저장되게 된다. 예를 들어 N이 4 이고 가장 윗 줄에 3 1 2 4 가 있다고 했을 때, 다음과 같은 삼각형이 그려진다.

N과 가장 밑에 있는 숫자가 주어져 있을 때 가장 윗줄에 있는 숫자를 구하는 프로그램을 작성하 시오. 단, 답이 여러가지가 나오는 경우에는 사전순으로 가장 앞에 오는 것을 출력하여야 한다.
[입력설명]
첫째 줄에 두개의 정수 N(1≤N≤10)과 F가 주어진다. N은 가장 윗줄에 있는 숫자의 개수를 의 미하며 F는 가장 밑에 줄에 있는 수로 1,000,000 이하이다.
[출력설명]
첫째 줄에 삼각형에서 가장 위에 들어갈 N개의 숫자를 빈 칸을 사이에 두고 출력한다. 답이 존재 하지 않는 경우는 입력으로 주어지지 않는다.
입력예제 1
4 16
출력예제 1
3 1 2 4
문제 풀이
코드
-
b배열에 콤비네이션값을 미리 저장해놓고, p배열에 조합을 넣는다. 이후 b와 p를 곱한 후, 누적된 sum의 값이 f인지 확인한다.
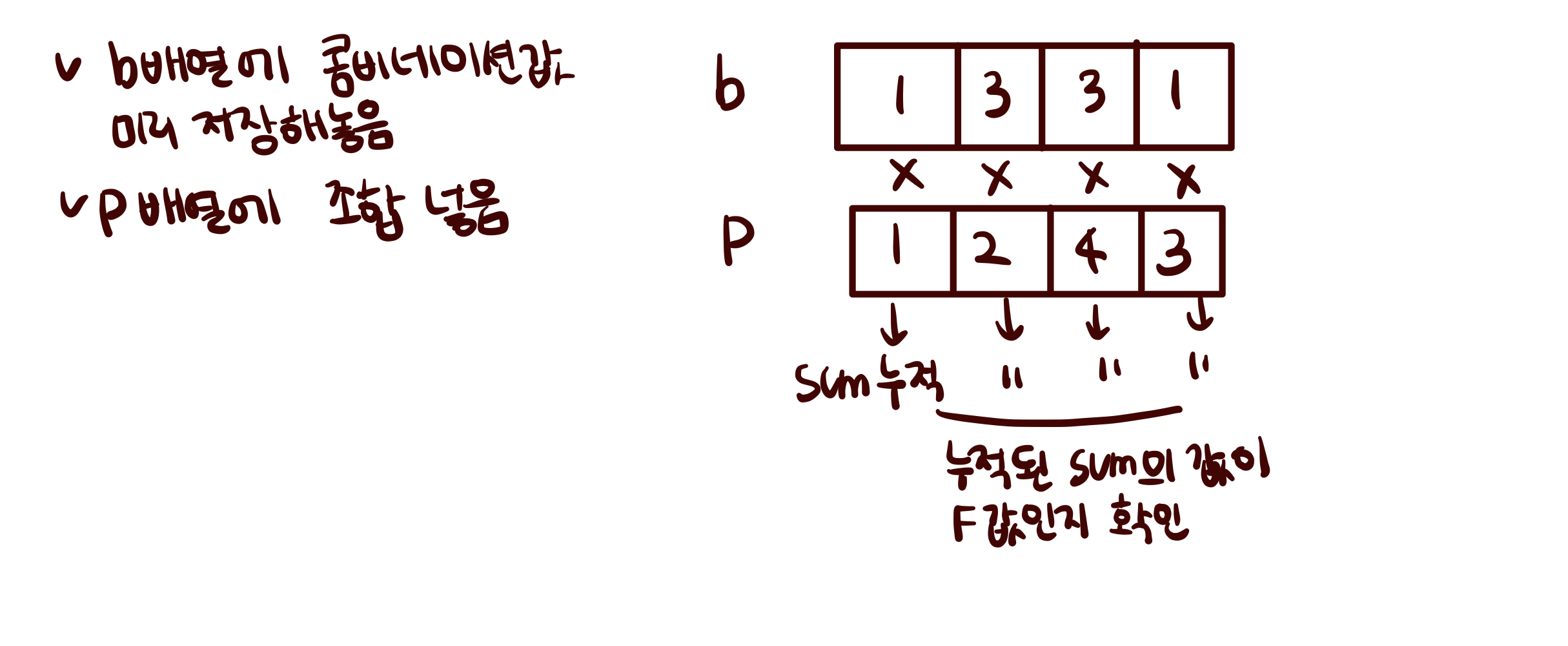
-
콤비네이션값은 N=4일 때 3C0(1) + 3C1(3) + 3C2(3) + 3C3(1)이다. 마찬가지로 N=5일 때는 4C0+4C1+4C2+4C3+4C4로 구할 수 있다.
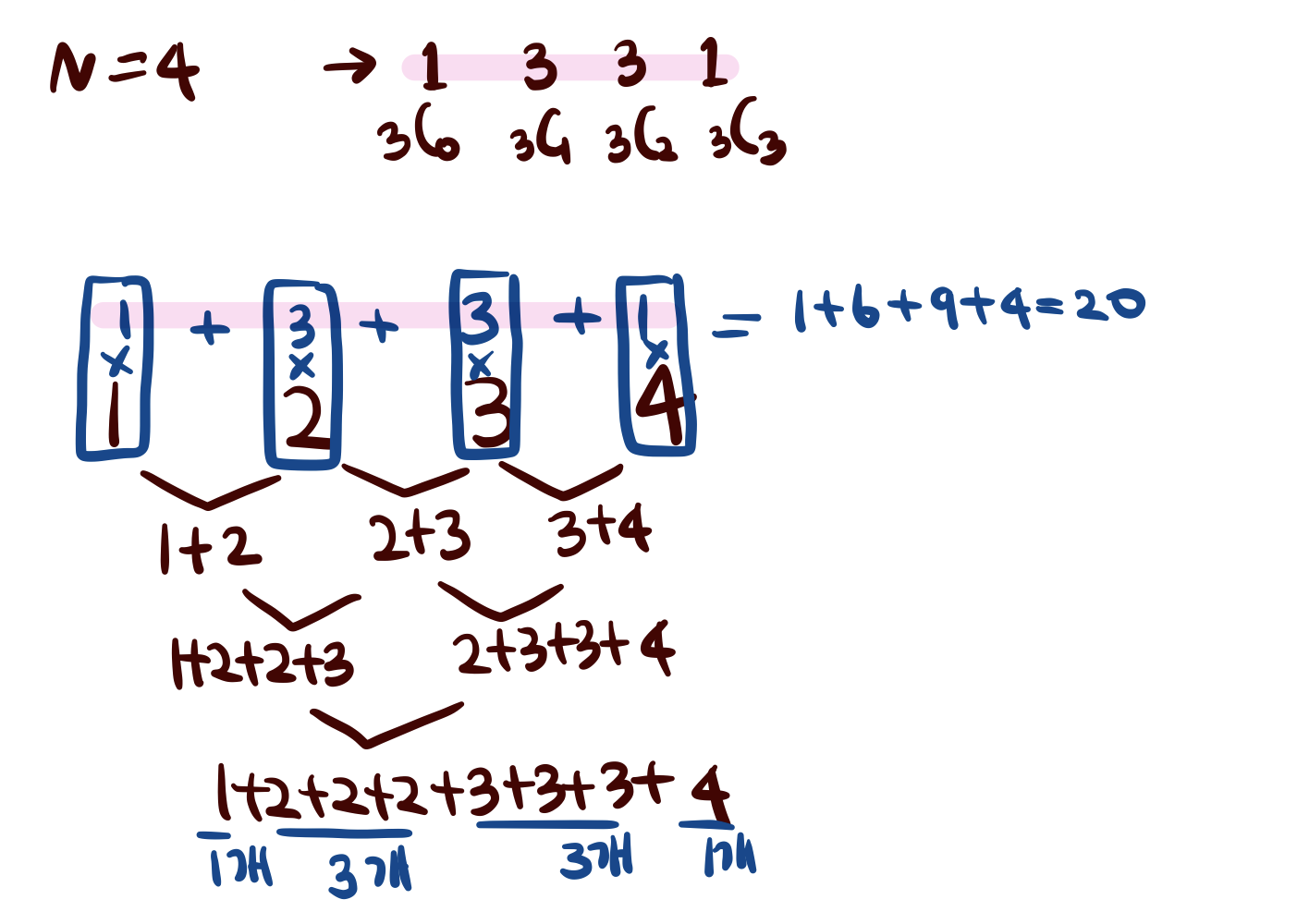
<html>
<head>
<meta charset="UTF-8">
<title>출력결과</title>
</head>
<body>
<script>
function solution(n, f){
let answer, flag=0;
let dy= Array.from(Array(11), ()=>Array(11).fill(0)); //1<=n<=10
let ch=Array.from({length:n+1}, ()=>0); //중복 허용 안될때 만들어주기
let p=Array.from({length:n}, ()=>0); //조합
let b=Array.from({length:n}, ()=>0); //콤비네이션값 미리 저장
//조합 수
function combi(n, r){
if(dy[n][r]>0) return dy[n][r];
if(n===r || r===0) return 1;
else return dy[n][r]=combi(n-1, r-1)+combi(n-1, r);
}
function DFS(L, sum){
//답이 있을 때 stop
if(flag) return;
// 순열 완성 되었을 때
if(L===n && sum===f){
answer=p.slice(); //깊은 복사
flag=1;
}
else{
for(let i=1; i<=n; i++){
//순열 돌아감
if(ch[i]===0){
ch[i]=1;
p[L]=i;
DFS(L+1, sum+(b[L]*p[L]));
ch[i]=0; //체크 풀어주기
}
}
}
}
//b배열 만들어줌(콤비네이션 값)
for(let i=0; i<n; i++){
b[i]=combi(n-1, i);
}
DFS(0, 0);
return answer;
}
console.log(solution(4, 16));
</script>
</body>
</html>
<!-- 방법2) push, pop 사용-->
<!--
<html>
<head>
<meta charset="UTF-8">
<title>출력결과</title>
</head>
<body>
<script>
function solution(n, f){
let answer, flag=0;
let dy= Array.from(Array(11), () => Array(11).fill(0)); //1<=n<=10
let ch=Array.from({length:n+1}, ()=>0);
let p=[];
let b=Array.from({length:n}, ()=>0);
//조합 수
function combi(n, r){
if(dy[n][r]>0) return dy[n][r];
if(n===r || r===0) return 1;
else return dy[n][r]=combi(n-1, r-1)+combi(n-1, r);
}
function DFS(L, sum){
// 순열 완성 되었을 때
if(L===n && sum===f){
if(flag) return;
answer=p.slice(); //깊은 복사
flag=1;
}
else{
for(let i=1; i<=n; i++){
//순열 돌아감
if(ch[i]===0){
ch[i]=1;
p.push(i); //push
DFS(L+1, sum+(b[L]*p[L]));
ch[i]=0; //체크 풀어주기
p.pop(); //pop(반드시 해줘야함)
}
}
}
}
for(let i=0; i<n; i++){
b[i]=combi(n-1, i);
}
DFS(0, 0);
return answer;
}
console.log(solution(4, 16));
</script>
</body>
</html>
-->

9/17
앞 문제 응용,
전체적인 그림그려가면서 생각해보고 문제풀기