프로그래머스에서 효율성 테스트를 통과하기 위해서는 시간복잡도도 신경써줘야한다. 아직까지는 낮은 레벨을 풀고있기 때문에 효율성 테스트를 통과하지 못해서 헤맸던 경험은 없지만, 나중을 대비해서 정리해둔다✍🏻
시간복잡도 개념을 찾다가 잘 설명된 영상 by 엔지니어대한민국이 있어서, 그내용을 정리한다.
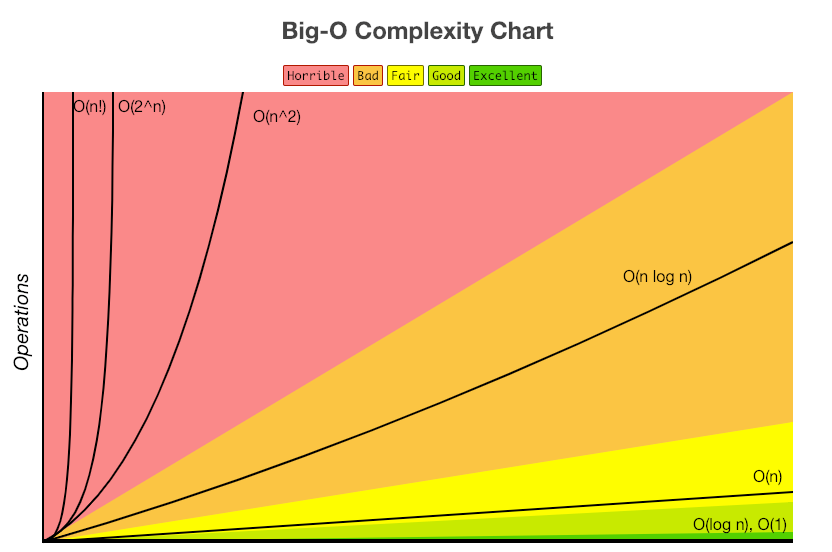
Big-O란?
- Big-O는 알고리즘의 성능(효율성)을 수학적으로 표현해주는 표기법이다. (algorithm efficiency)
- Big-O를 통해 알고리즘의 시간과 공간 복잡도를 표현할 수 있다. (Time & Space complexity)
- Big-O표기법은 알고리즘의 실제 러닝타임을 표시하는것이라기 보다는 데이터나 사용자의 증가율에 따른 알고리즘의 성능을 예측하는 것이 목표이기 때문에, 상수와같은 숫자는 모두 1회로 친다. (Describes the growth rate of algorithms)
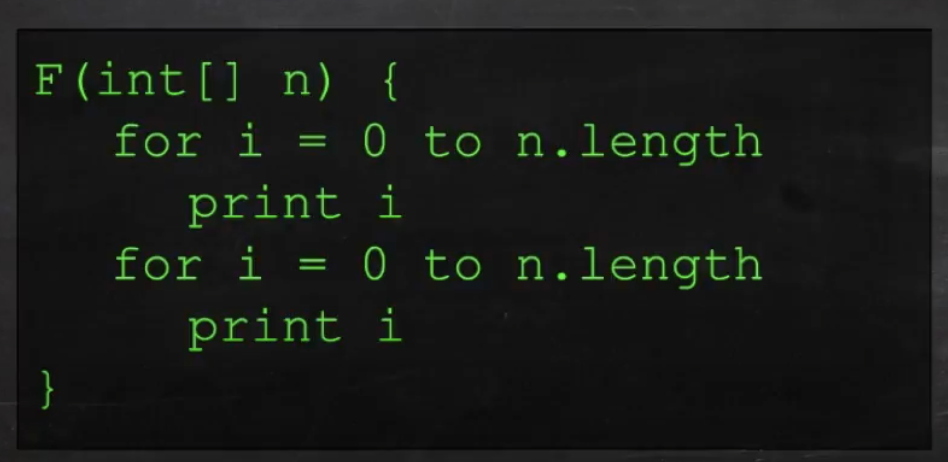
즉, 위 코드의 정확한 복잡도는 O(2n)이지만, big o 표기법에 따라 2는 떼고 O(n)으로 표시한다. big o표기법은 실제 알고리즘의 러닝타임을 재기 위해 만든 것이 아닌, 장기적으로 데이터 증가에 따른 시간의 증가율을 예측하기 위해 만들어진 표기법이기 때문이다.

마찬가지로, 위 코드에서도 O(n²+n²)이 아닌 O(n²)으로 표시한다. 둘다 차원이 같기 때문이다.
O(1): constant time
개념
입력 데이터의 크기와 상관없이, 언제나 일정한 시간이 걸리는 알고리즘이다.

위 함수에서, 배열 첫번째의 값이 0인지 확인하고, 0이면 true, 아니면 false를 리턴한다. 무조건 배열의 첫번째 방을 확인하기 때문에 배열의 크기가 중요하지 않고, 언제나 일정한 속도로 결과를 반환한다. 이 경우 O(1)의 복잡도를 가진다고 표현한다.
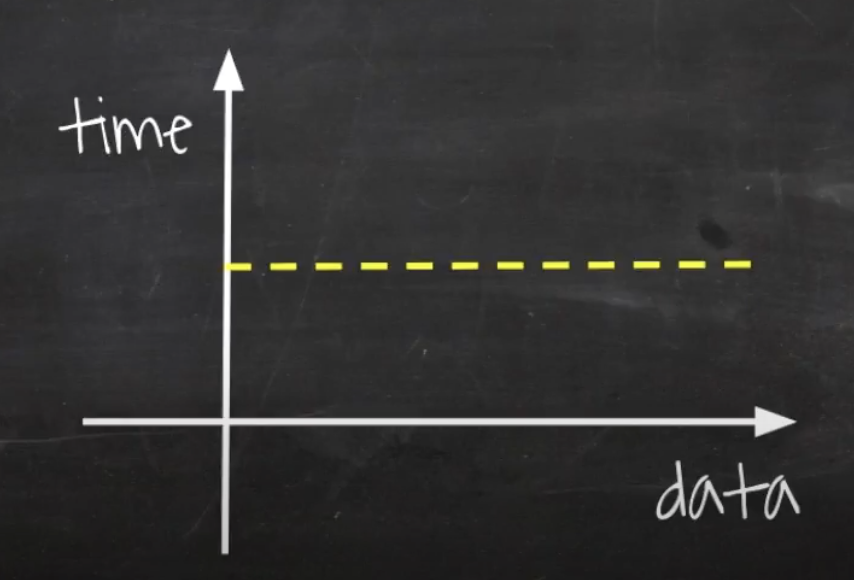
그래프
데이터가 증가함에 따라 성능의 변함이 없다.
O(n): linear time
개념
입력 데이터에 크기에 비례해서 처리시간이 걸리는 알고리즘을 표현할 때 사용한다.
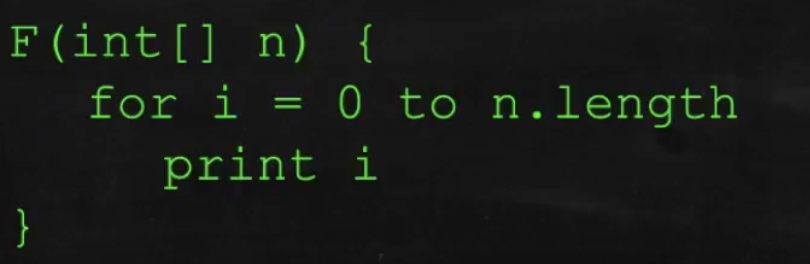
여기서, n개의 데이터를 받으면 n번 루프를 돈다. 따라서, n이 1 늘어날 때 마다 처리가 한번씩 늘어나서 n의 크기만큼 처리 시간이 걸린다.
그래프
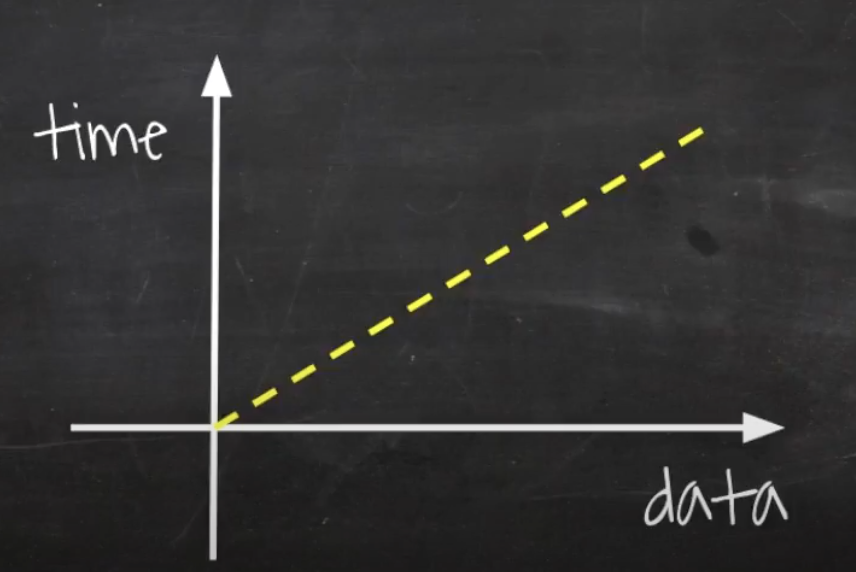
데이터가 증가함에 따라 비례해서, 처리 시간도 같이 증가한다. 데이터와 시간이 같은 비율로 증가하기 때문에 그래프가 직선으로 표시된다.
O(n²): quadratic time

n을 돌리면서, 그안에서 n으로 루프를 또 돌릴 때 n²가 된다.

n개의 데이터를 받으면, 첫번째 루프에서 n번 돌면서 각각의 엘리먼트에서 n번씩 또 도니까 n * n을 가지는 면적만큼 된다. 만약, n이 한개씩 늘어날 때 마다 아래 한줄, 오른쪽 한줄이 느니까 데이터가 커지면 커질수록 처리시간에 부담이 커진다.
그래프
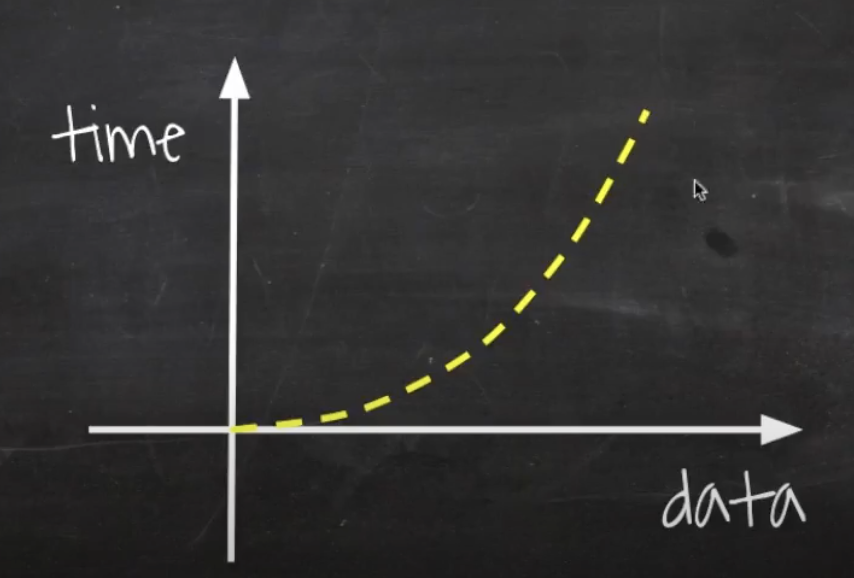
데이터가 늘어날수록, 급격하게 수직에 가까워진다.
O(nm): quadratic time

위의 n²과 달리, n을 두번 돌리는게 아니라 n을 m만큼 돌린다. 루프모양 두개가 겹쳐있다고 무조건 n²이라고 생각하면 안된다!(실수 주의❎)
m은 아주 작을 수도 있고, 아주 클 수도 있기 때문에 변수가 다르다면 big o표기법에도 다르게 표시해줘야한다.
그래프
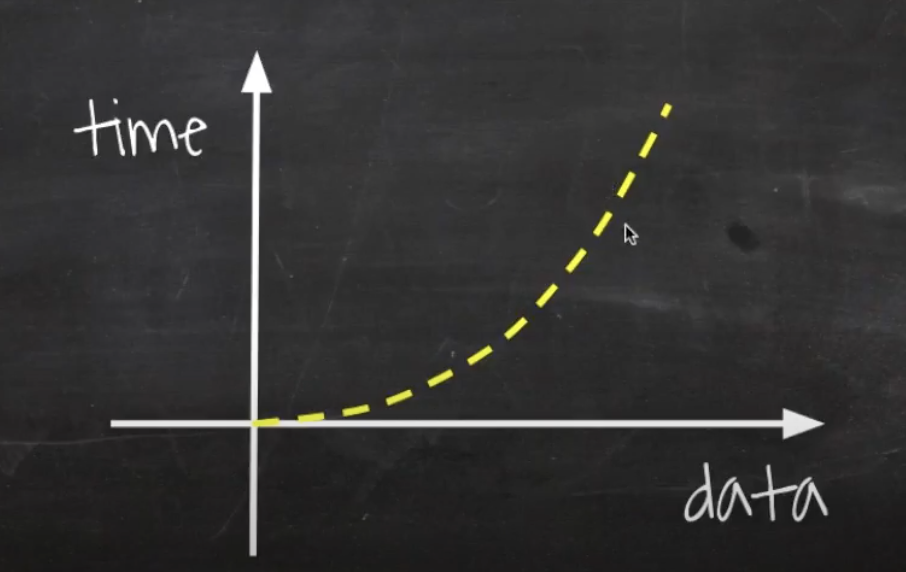
nm도 n²과 마찬가지로, 데이터가 증가할수록 그래프가 점점 수직에 가까운 모양이 된다.
O(n³): polynomial/cubic time

n을 3종으로 돌리면 n³이 된다. n²은 면적이 되고, n³은 n²을 n만큼 더 돌리니까 큐빅 모양이 된다.

그래프

n²과 비슷하지만, 데이터가 늘어날 때마다 가로 세로의 높이까지 더해지니까 n²보다 더 급격하게 처리시간이 늘어난다.
O(2^n): exponential time
피보나치수열을 살펴보자
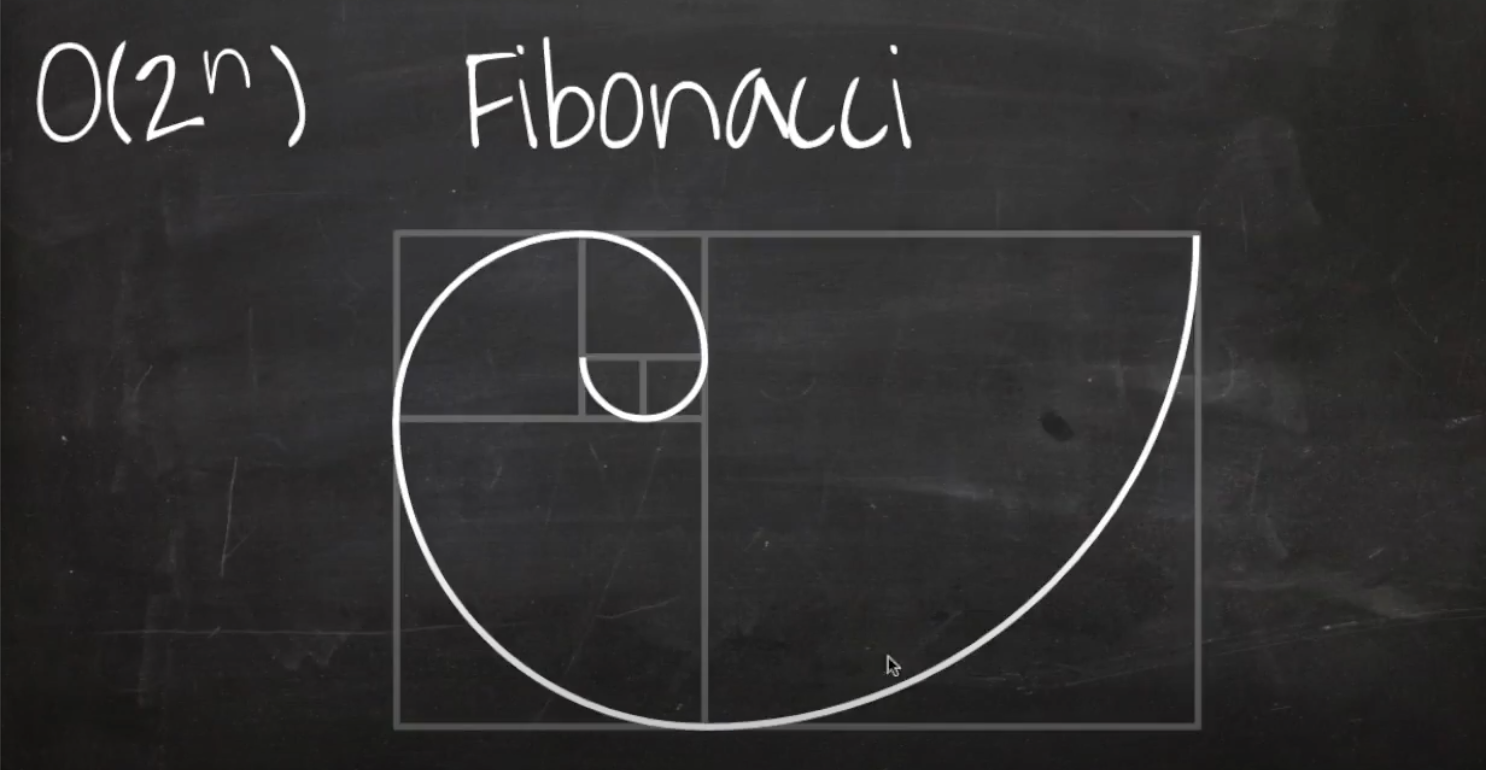
피보나치 수열은 위처럼 나선형이 그려지는 수열이다. 수학적으로 접근해보자.
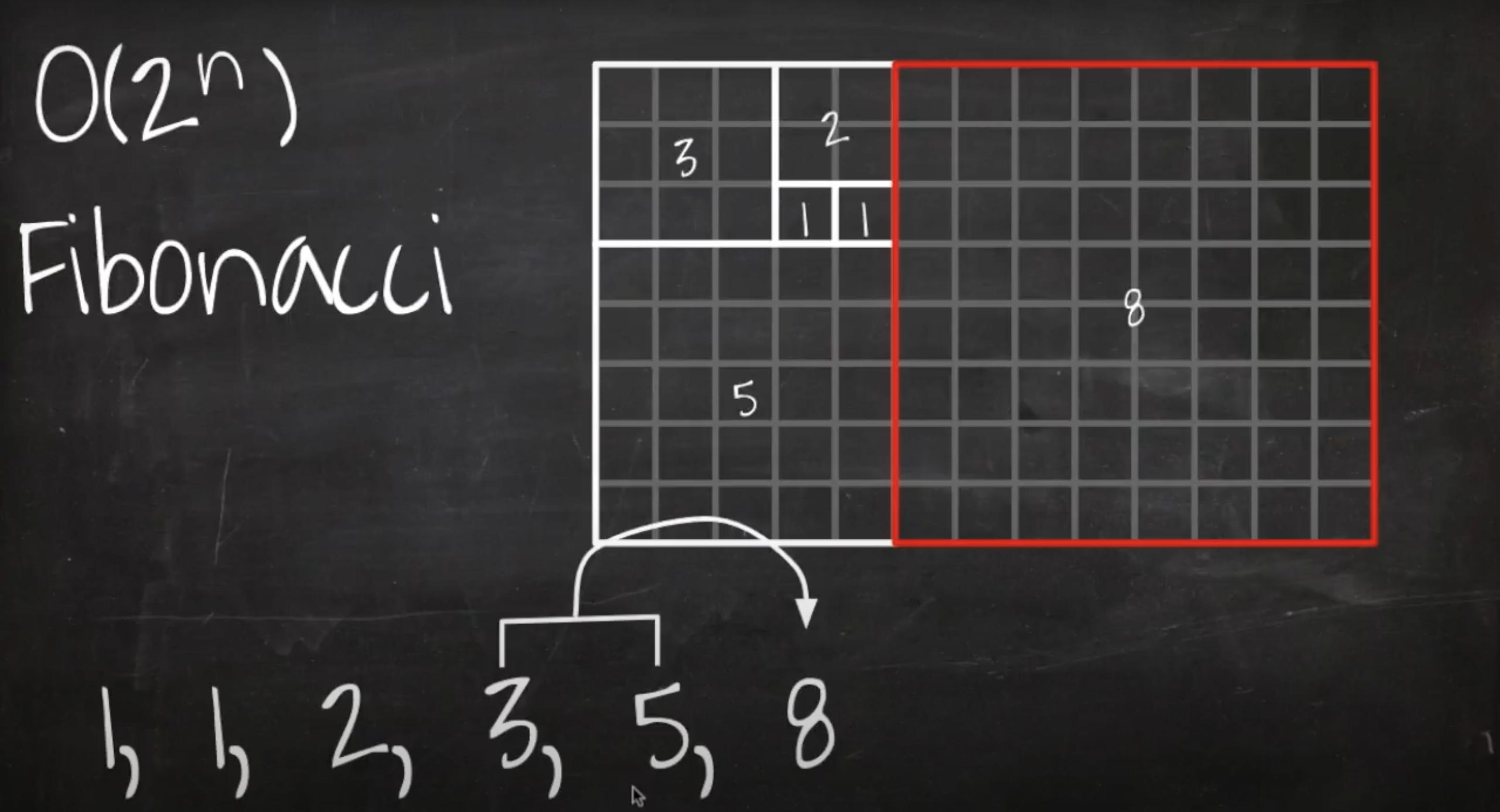
위의 논리를 코드로 구현해보자.

재귀함수로 구현하면 위 코드와 같다. 함수를 호출할 때마다 바로 전 숫자와 전전 숫자를 알아야 더할 수 있기 때문에, 함수가 호출될 때 마다 두번씩 재귀함수를 호출한다.

따라서, 위와 같이 트리의 높이만큼 반복한다.
그래프
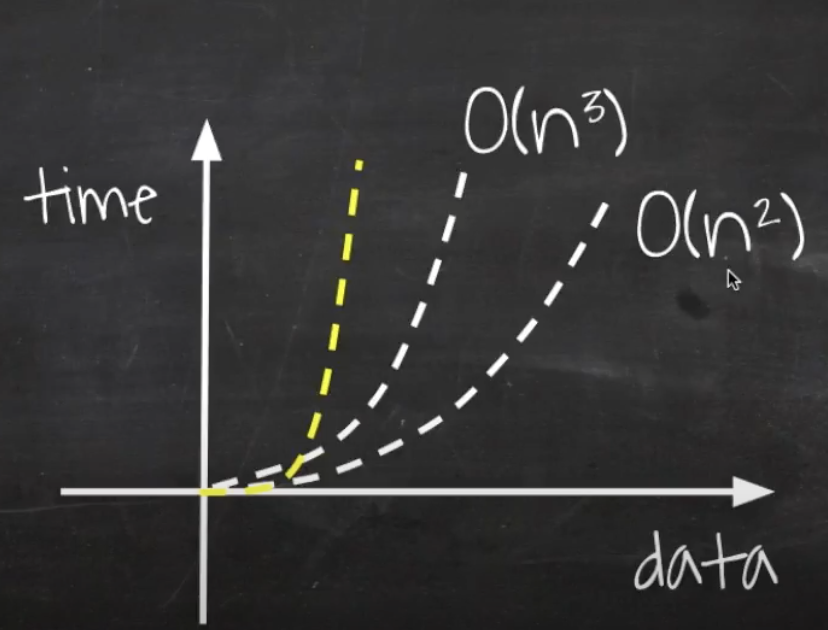
n³보다 데이터 증가에 따라 처리시간이 현저하게 늘어난다.
O(m^n): exponential time
m개씩 n번 늘어나는 알고리즘
O(log n)
이진검색을 하면, 함수가 한번 호출될 때마다 중간값을 기준으로 절반은 검색 영역에서 제외시켜버리기 때문에 순차검색에 비교해서 속도가 현저하게 빠르다.
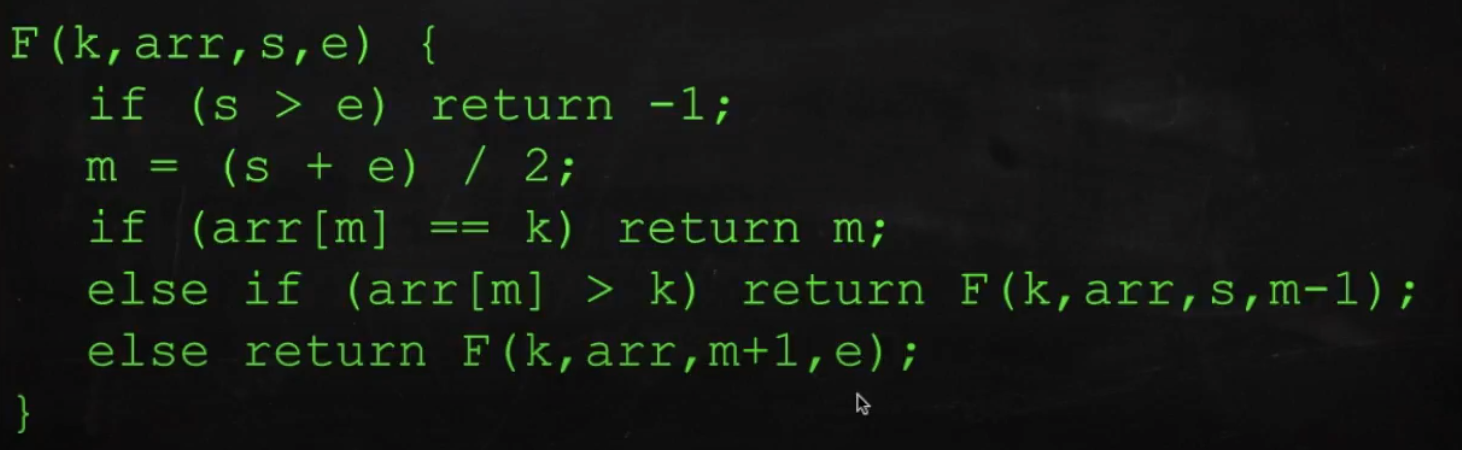
그래프
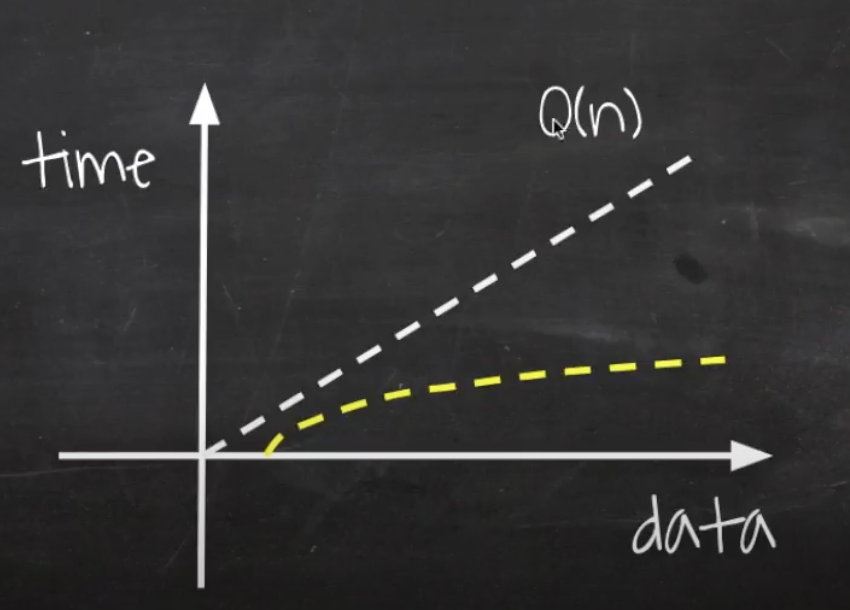
O(n)보다 훨씬 적게 든다. 그리고 데이터가 증가해도 성능이 크게 차이나지 않는다.
O(sqrt(n))
sqrt는 제곱근이다.

16의 정사각형을 채워서, 맨 위의 한줄만큼만 실행한다.
시간 복잡도 그래프