[Java] 스도쿠 보드 알고리즘

1. 문제 설명

9 x 9 크기의 스도쿠 보드가 주어진다.
즉 81칸의 크기로 주어지는데 칸의 번호를 입력받아 행, 열, 그룹 번호를 출력하라

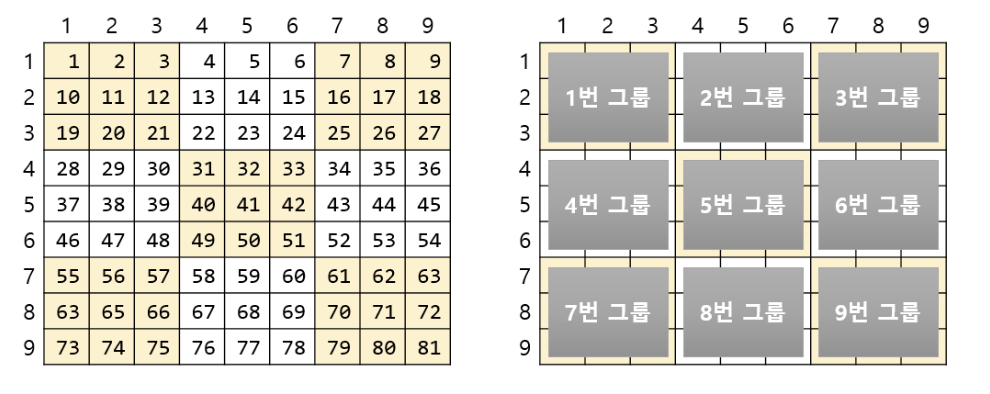
입력 형식

첫 줄에는 테스트케이스의 수 T가 주어진다. T는 1이상 100이하의 자연수 중 하나이다.

각 테스트케이스에는 칸의 번호가 1부터 81까지의 자연수로 공백없이 한 줄에 주어진다.

출력 형식

테스트케이스의 첫 줄에는 `Case #%d:` 형식으로 테스트케이스의 번호를 출력
테스트케이스의 두 번째 줄에는 칸 번호의 행, 열, 그룹 번호를 구분된 세 개의 자연수로 출력

2. 알고리즘 접근

2차원 반복문을 탐색하여 위치를 찾아내는 방법은 비효율적, 수학알고리즘 사용

행, 열 번호 구하기

규칙성 검사
칸의번호의 행 번호와, 열 번호를 나열해보자
1 ~ 9의 값을 생각해보면
행(r) : 1, 1, 1, 1, 1, 1, 1, 1, 1
열(c) : 1, 2, 3, 4, 5, 6, 7, 8, 9
10 ~ 18
행(r) : 2, 2, 2, 2, 2, 2, 2, 2, 2
열(c) : 1, 2, 3, 4, 5, 6, 7, 8, 9의 특징을 가진다
위 규칙을 풀어보면

행 번호는 규칙적인 일정한 마디가 생긴다 (몫과 관련이 있다)
열 번호는 순환하는 일정한 주기가 생긴다 (나머지와 관련이 있다)
행 번호 : r / 9
열 번호 : r % 9

그룹 번호 구하기

규칙성 검사
각 행과 열에 대해서 가장 왼쪽 그룹의 번호를 나열해보자
1 ~ 9의 값을 생각해보면
행(r) : 1, 1, 1, 4, 4, 4, 7, 7, 7
열(c) : 1, 1, 1, 2, 2, 2, 3, 3, 3

즉 행 번호를 알면 각 행의 처음 등장하는 그룹번호를 알 수 있다
열 번호를 알면 해당 행에서 몇 번째 그룹인지 알 수 있다
각 행의 첫 그룹번호를 구하고 해당 행의 몇번째 그룹인지를 구해 더하면 된다

위의 자세한 코드 구현은 아래 소스코드를 참고하자

3. 알고리즘 풀이

import java.util.Scanner;

public class Q4A {
    public static final Scanner sc = new Scanner(System.in);


    private static void testCase(int caseIndex) {
        int index = sc.nextInt(); // 칸의 번호 입력
        SudokuBoard board = new SudokuBoard(); // 스도쿠 객체 생성

        int row = board.getRowByIndex(index); // 행 계산
        int col = board.getColByIndex(index); // 열 계산
        int group = board.getGroupByPosition(row, col); // 그룹번호 계산하기

        // 정답을 출력한다
        System.out.printf("Case #%d:\n", caseIndex);
        System.out.printf("%d %d %d\n", row, col, group);
    }

    public static void main(String[] args) {
        int caseSize = sc.nextInt(); // 테스트케이스 입력

        for(int caseIndex = 1; caseIndex <= caseSize; caseIndex++){
            testCase(caseIndex);
        }
    }
}

class SudokuBoard{
    static final int MAX_ROW = 9;
    static final int MAX_COL = 9;

    // 칸의 번호로 행을 계산하는 인덱스
    public int getRowByIndex(int index){
        return (index - 1) / 9 + 1;
    }

    // 칸의 번호로 열을 계산하는 인덱스
    public int getColByIndex(int index){
        return (index - 1) % 9 + 1;
    }
    // 칸의 번호로 그룹 번호를 계산하는 인덱스
    public int getGroupByIndex(int index){
        int r = getRowByIndex(index);
        int c = getColByIndex(index);
        return getGroupByPosition(r, c);
    }
    // 칸의 위치로 그룹 번호를 계산하는 메소드
    public int getGroupByPosition(int row, int column) {
        int left = ((row - 1) / 3) * 3 + 1; // 행의 가장 왼쪽 그룹 번호(row행 , 1~3열)
        int offset = ((column - 1) / 3);  // 실제 이 열이 속한 그룹의 위치
        // 열마다 그룹번호를 할당하는데 행 + 열로 그룹번호를 주기에 행에서 1based를 이미 주었기 때문에 +1을 하지 않는다
        return left + offset;
    }

    // 문제와 예외로 구현해보기
    // 칸의 위치(행, 열)로 칸의 번호를 계산하는 메소드
    public int getIndexByPosition(int row, int column) {
        return ((row - 1) * 9) + column;
    }
}

지금까지 이런 유형의 문제는 2차원 배열로 정의하여 순회하며 값을 구하는 방법만
알고 있었는데 이렇게 몫과 나머지의 특징을 이용해 수학 공식으로 풀어보니 새롭다
인덱스의 위치를 유의하면서 수학 공식을 잘 이용하자
성능 개선에 도움을 준다.