[Java] 픽셀 수 세기

Minuuu·2023년 1월 17일
알고리즘

알고리즘

목록 보기
4/36

목적

단순 구현이 아닌 접근 방법과 그에 대한 문제점 파악을 통해 코드 개선을 보여준다
위를 통한 구현으로 어떻게 코드를 개선할 수 있는지에 대한 설명을 통해 초보자들도 쉽게 이해할 수 있는 글
간단한 요약이 아닌 헷갈리는 부분도 최대한 세밀한 설명

목차

  1. 문제 설명
  2. 알고리즘 접근방법
  3. 1차 구현
  4. 문제점 파악 및 최적화
  5. 최종 코드

1. 문제 설명

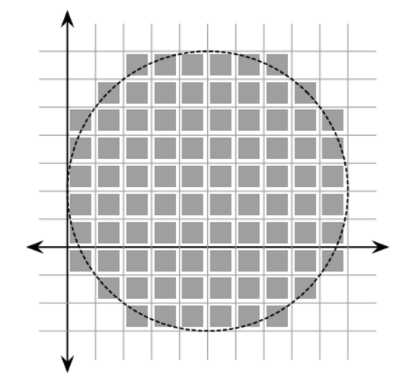
컴퓨터의 이미지는 2차원 배열로 저장된다
영상을 구성하는 하나의 픽셀은 정사각형 형태로 존재하며 이 픽셀들이 모여 2차원 배열의 모양을 구성
반지름이 5 픽셀인 원을 그리면 위와 같다
반지름이 R픽셀인 원이 포함하는 픽셀 수를 구해보자
입력 : 계산하고자 하는 원의 반지름의 픽셀 수 R이 주어진다.
         R은 1이상 10만 이하의 자연수이다.

2. 알고리즘 접근방법

위 그림을 보면 알 수 있는 정보는 실제로 원안에 있는 픽셀들은 다음과 같은 특징을 가진다

  • 네 점이 원 안에 존재하거나(원 안)
  • 원과 겹치는 영역이 존재하면서 두개 이상의 변이 원의 외곽선과 교차(원 테두리)

최적화 아이디어 1. 원의 특징을 이용하자!

자 그러면 생각해보자 우리는 픽셀 수를 구하는 것이 목적이다
그러면 원의 위치가 픽셀수의 관계가 있을까?? => 관계가 없다
즉 우리는 원의 중앙을 (0, 0) 지점으로 잡고 계산해도 상관없다
왜 굳이 원의 중앙을 잡나요?? 라고 물어본다면

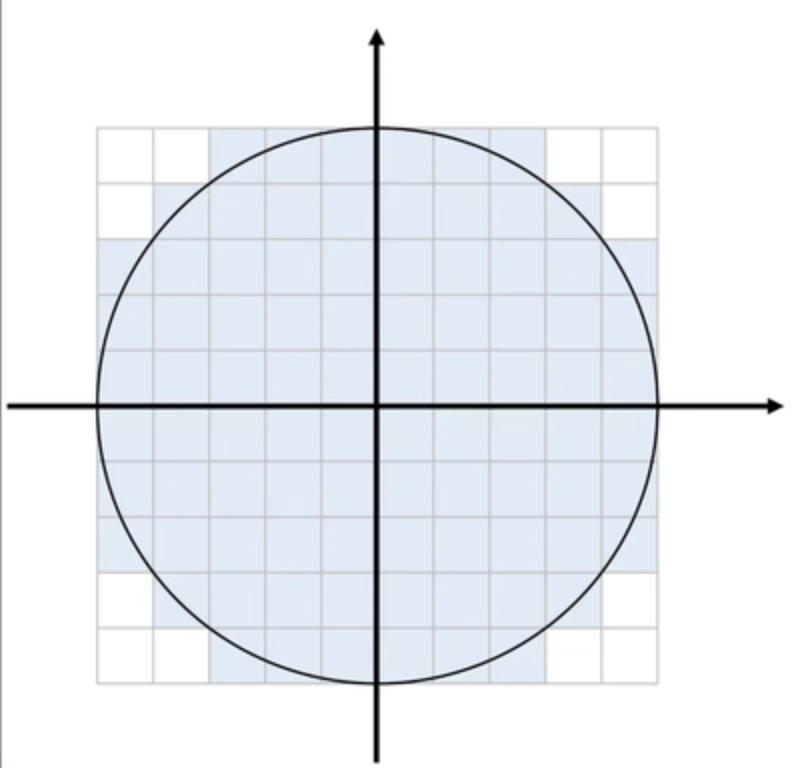
이렇게 원의 중앙을 잡고 원은 사분면을 대칭한 도형이기 때문에
우리가 1사분면에 해당하는 픽셀수만 계산하면 2, 3, 4분면의 픽셀수도 같을 것이다
즉 우리는 1사분면에 픽셀수를 계산해 x 4 해주면 되는 것이다
그렇다면 1사분면에서 양수 좌표만 고려한 계산이 가능하다!!!

최적화 아이디어 2. 우리가 몇 픽셀까지 고려해야하지??

문제에서 반지름으로 주어졌지 픽셀의 좌표를 제한하지 않아 이론상
픽셀은 무한으로 주어질 수 있지만
어차피 문제풀이를 위해 필요한 픽셀은 원과 접하거나 원 내부의 픽셀이니
그 좌표는 R을 넘기지 않을 것이다(많아봤자 R + 1)에 해당하는 픽셀만 고려

구현 아이디어

R2R^2개의 격자들 중 원에 포함되는 픽셀의 수를 세자

  • 각 격자를 구분할 수 있는 기준 : 왼쪽 아래 점 좌표

그러면 우리가 픽셀을 count하는 문제로 보이는데
count할 대상의 기준이 필요 -> 격자의 네 점중 '왼쪽 아래 점의 좌표'를 기준으로 잡자

픽셀이 원안에 있는 조건

네 점 모두 원 안에 있거나, 두개 이상의 변과 교차한다 + 영역 교차
= 왼쪽 아래 점(x, y)이 원안에 있다
= (x−0)2+(y−0)2<R\sqrt{(x-0)^2 + (y-0)^2} < R

왼쪽 아래의 점과 원점(0, 0)의 거리를 구해 < R(반지름)을 구하면 조건이 성립하는 것이다
-> 원점을 쓰면 좋은이유 ㅎ x2+y2x^2 +y^2만 결론적으로 하면된다

3. 1차 구현

import java.util.Scanner;

public class Q2H {
    public static final Scanner scanner = new Scanner(System.in);

    /**
     * 왼쪽 아래 좌표가 (x,y)인 픽셀이 반지름 R인 원에 포함되는가?
     * @param x
     * @param y
     * @param R
     * @return  포함된다면 true, else false
     */
    public static boolean isInside(long x, long y, long R)
    {
        // 문제에서 주어진 반지름이 10만이기에 좌표가 10만 가까이 나올 수 있다
        // 이를 제곱하면 100억이 나온다 -> int는 21억의 범위이기에 long 사용
        long sqd = x * x + y * y; // 왼쪽 아래의 점과 원점(0, 0)사이의 거리
        return sqd < R*R;
    }

    public static void testCase(int caseIndex) {
        long R = scanner.nextLong();
        long count = 0;
        for(int x = 0; x <= R; x++){
            for(int y = 0; y <= R; y++){
                // <x, y> := (0, 0) ~ (R, R) 까지의 모든 좌표가 한번씩 나온다
                if(isInside(x, y, R)){
                    // <x, y>가 왼쪽 아래점인 픽셀들 중 원 내부에 있는 모든 픽셀
                    count++;
                }
            }
        }
        System.out.printf("#%d\n", caseIndex);
        System.out.println(count * 4);
    }

    public static void main(String[] args) throws Exception {
        int caseSize = scanner.nextInt();

        for (int caseIndex = 1; caseIndex <= caseSize; caseIndex += 1) {
            testCase(caseIndex);
        }
    }
}

4. 문제점 파악 및 최적화

그러나 위의 풀이는 시간 초과가 걸린다
시간복잡도가 O(R2)O(R^2)이다 이때 R이 대략 10만이니
100억이 나오기에 1~ 2초 내에 나올 수없다

최적화 아이디어1

x좌표가 같은 격자끼리 하나의 그룹으로 묶어보자.
각 그룹별로 가장 위의 격자의 위치를 알 수 있다면?
그 아래의 격자 수는 자명 해진다

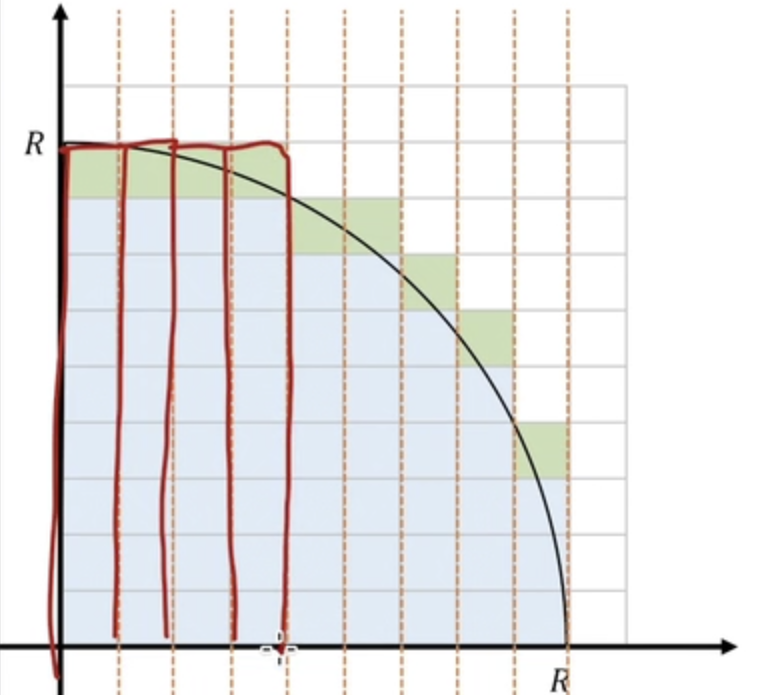
위와 같이 세로로 묶으면 이는 직사각형의 크기와 같다(폭이1이니)
= 직사각형의 높이 = x축 별 픽셀 수
높이를 아는 방법은 R에서 내려오다가 원에 포함되는픽셀을 만났을 때
그 픽셀의 y + 1 값(y : 네모의 왼쪽 아래 점)

public static void testCase(int caseIndex) {
		long R = scanner.nextLong();
		long sum = 0;
		for(int x = 0; x <= R; x++){
			for(long y = R; y >=0; y--){
				if(isInside(x, y, R)){
					// y := x좌표에서 위에서부터 내려오다가 
                    // 최초로 원에 포함되는 픽셀의 y좌표
					long h = y + 1; // 지정한 부분의 높이
					sum += h;
					break;
				}
			}
		}
		System.out.printf("#%d\n", caseIndex);
		System.out.println(sum * 4);
	}

그러나 이도 픽셀을 찾는 과정에서 O(R^2)의 시간복잡도를 가져 안된다
-> 이 아이디어를 좀 더 개량해보자

최적화 아이디어2

문제의 성질을 더 이용해보자
세로로 묶은 막대들은 1사분면에서 x좌표가 증가할 수록 y 좌표가 감소한다(위의 그림 참고)
즉, 각 그룹의 높이는 내림차순 배열과 같다 -> 이를 어떻게 활용하지?
우리가 위 최적화 아이디어1에서는
그냥 무작정 위에서 내려와서 원에 포함된 픽셀을 찾으려고 했다

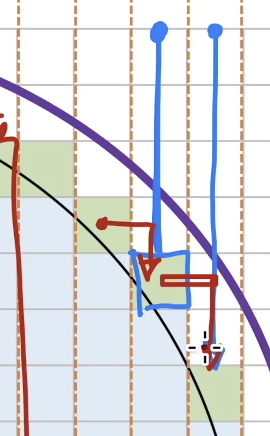
파랑 : 기존의 방법
빨강 : 최적화 한 방법
빨강 : 왜 굳이 무작정 내려오지 그냥 어차피 내림차순이니까
이전기둥값을 기준으로 내려오면 되는거 아냐? -> 이 방법으로 접근

	public static void testCase(int caseIndex) {
		long R = scanner.nextLong();
		long sum = 0;
		long y = R; // y를 R로 초기화하고
		for(int x = 0; x <= R; x++){
			for( ; y >=0; y--){ // R을 기준으로 계속 --한다
				if(isInside(x, y, R)){
					long h = y + 1; // 지정한 부분의 높이
					sum += h;
					break;
				}
			}
		}
		System.out.printf("#%d\n", caseIndex);
		System.out.println(sum * 4);
	}

위 코드의 시간 복잡도를 계산해보면
먼저 if문에서 단위 계산하여 상수 O(1)의 시간 복잡도를 가진다
아무리 많이 이동해봐야 x좌표이동, y좌표의 이동만큼만 수행할 것이다
O(1) x (R + R) = O(R)의 시간 복잡도를 가지게 된다

5. 최종 소스코드

import java.util.Scanner;

public class Q2H {
    public static final Scanner scanner = new Scanner(System.in);

    /**
     * 왼쪽 아래 좌표가 (x,y)인 픽셀이 반지름 R인 원에 포함되는가?
     * @param x
     * @param y
     * @param R
     * @return  포함된다면 true, else false
     */
    public static boolean isInside(long x, long y, long R)
    {
        // 문제에서 주어진 반지름이 10만이기에 좌표가 10만 가까이 나올 수 있다
        // 이를 제곱하면 100억이 나온다 -> int는 21억의 범위이기에 long 사용
        long sqd = x * x + y * y; // 왼쪽 아래의 점과 원점(0, 0)사이의 거리
        return sqd < R*R;
    }

    public static void testCase(int caseIndex) {
        long R = scanner.nextLong();
        long sum = 0;
        long y = R;
        for(int x = 0; x <= R; x++){
            for( ; y >=0; y--){
                if(isInside(x, y, R)){
                    long h = y + 1; // 지정한 부분의 높이
                    sum += h;
                    break;
                }
            }
        }
        System.out.printf("#%d\n", caseIndex);
        System.out.println(sum * 4);
    }

    public static void main(String[] args) throws Exception {
        int caseSize = scanner.nextInt();

        for (int caseIndex = 1; caseIndex <= caseSize; caseIndex += 1) {
            testCase(caseIndex);
        }
    }
}

후기

초보자에게 쉽게 이해하려고 세세하게 적었지만 문제 자체가 어렵다 보니 이해하기 힘들 것으로 보이지만 세세하게 읽고 코드도 세세하게 본다면 이해가 될겁니다!!
단순히 전엔 구현만 하면 되겠다 생각했는데 데이터 범위에 대한
자료형 선택과 이에 대한 시간 복잡도 고려의 중요성을 알게 됐습니다

profile
Minuuu
꾸준히 한걸음씩 나아가려고 하는 학부생입니다 😄
이전 포스트

[Java] 점 사이의 거리

다음 포스트

[Java] 연속적인 수열 검사

0개의 댓글