스택(Stack)

팬케이크를 차곡차곡 쌓을 때, 방금 만든 팬케이크를 맨 위에 쌓게 된다. 맨 위에 놓인 팬케이크를 먹는 방식을 '스택'에 비유할 수 있다. 스택은 배열이 수직적으로 쌓여있는 것으로, 배열에서 요소를 추가하거나 삭제할 때 마지막으로 추가된 것부터 처리한다. 이를 "LiFo"라고 한다
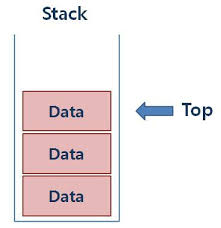
👉 새로운 요소는 스택 위에 차곡차곡 쌓이고, 스택의 맨 위에서만 요소를 읽거나 삭제할 수 있다
예) 웹 브라우저의 '뒤로가기'
📒 '뒤로가기'는 웹페이지 히스토리 스택의 맨 위에서 한 페이지를 가져가는 것이디 때문. Ctrl+Z도 스택에 포함
큐(Queue)

정류장에서 버스를 타기 위해 여러 사람들이 일렬로 서 있다고 가정하면, 맨 앞 줄에 있는 사람부터 순서대로 버스에 탈 것이다. 이러한 방식은 '큐'에 비유될 수 있다. 줄에 가장 뒤에 서서 기다린 사람은 버스에서도 가장 마지막에 탑승하게 되는 것처럼 가장 나중에 '큐'에 입장한 요소가 제일 마지막에 큐에서 나가는 요소가 된다. 이를 "FiFo"라고 한다
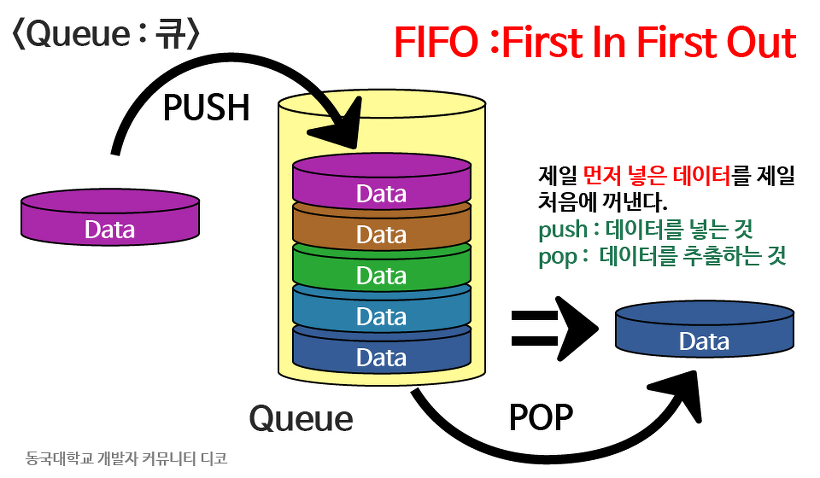
👉 큐는 줄 서기와 같다. 새로운 요소는 '큐'의 맨 뒤에 추가되고, 큐위 맨 앞에 있는 요소만 읽거나 삭제할 수 있다
예) 이메일 전달 혹은 푸쉬 알림 기능, 쇼핑몰에서 선착순으로 주문을 처리하는 방식, 콜센터의 백엔드 등
데크(deque)
deque는 앞과 뒤에서 데이터를 처리할 수 있는 양방형 자료형으로, 스택처럼 써도 되고 큐처럼 써도 된다. 파이썬의 collections.deque 모듈은 deque 자료형을 생성하는 모듈이다
🕦 문제
시계방향으로 1~5가 적힌 다이얼이 있으며 현재 가리키는 눈금은 1일 떄, 오른쪽으로 2칸 돌려 가리키는 눈금이 4가 되도록 하려면 어떻게 해야 할까?
현재: [1, 2, 3, 4, 5]
출력 예시: [4, 5, 1, 2, 3]
✅ 풀이
deque(a)로 deque 객체를 만든 후 rotate() 함수를 사용하여 2만큼 오른쪽으로 회전하면 첫 값이 4를 가리키게 된다. 마찬가지로 왼쪽으로 2만큼 회전하여 3을 가리키려면 2 대신 -2를 입력하면 된다
from collections import deque
a = [1,2,3,4,5]
q = deque(a)
q.rotate(2) #시계방향 회전은 양수, 그 반대는 음수
result = list(q)
print(result)list와 비슷한 deque
deque의 사용 예시
from collections import deque
d = deque([1,2,3,4,5])
d.append(6)
#print(d) #deque([1, 2, 3, 4, 5, 6])
d.appendleft(0)
#print(d) #deque([0, 1, 2, 3, 4, 5, 6])
print(d.pop()) #6
print(d) #deque([0, 1, 2, 3, 4, 5])
print(d.popleft()) #0
print(d) #deque([1, 2, 3, 4, 5])📁 deque는 list와 매우 비슷하다. 스택과 큐로 사용할 수 있는 메서드도 대부분 일치한다. 다만, deque에는 다음과 같은 메서드가 더 있다
- appendleft(x): 데크 왼쪽에 x 추가
- popleft(): 데크 왼쪽에서 요소를 제거
예를 들어 리스트에서는 첫 번째 요소를 삭제할 때 pop(0)을 사용하지만, deque는 popleft()를 사용한다
⭐ deque 장점
- deque는 list보다 속도가 빠르다. pop(0)와 같은 메서드를 수행할 때 리스트라면 O(N) 연산을 수행하지만, deque는 O(1) 연산을 수행하기 때문이다
- 스레드 환경에서 안전하다
빅오
- O(1) - 입력의 크기와 상관 없이 항상 같은 시간이 걸리는 알고리즘이다. 리스트나 딕셔너리의 데이터에 접근할 때 O(1)의 시간 복잡도를 갖는다
- O(logN) - 문제를 해결하는데 필요한 단계들이 연산마다 줄어드는 알고리즘이다. 이진탐색, 힙 삽입/삭제 등이 O(logN)의 시간 복잡도를 갖는다
- O(N) - 한번의 반복을 수행하고 완료되는 선형 탐사가 O(N)의 시간 복잡도를 갖는다
- O(N^2) - 2중 반복을 돌게되는 알고리즘은 O(N^2)의 시간 복잡도를 갖는다
