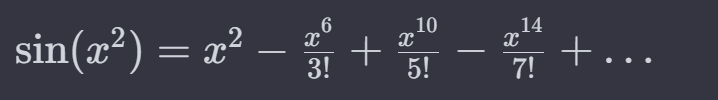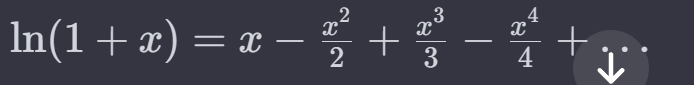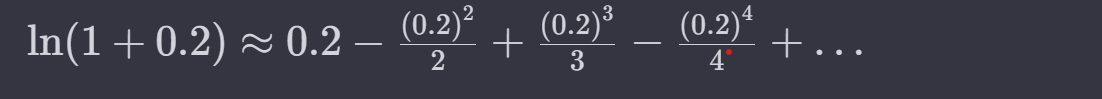테일러 급수

서론

I always wondered why Euler's identity is true. Why the
$e^ix$ is represented as $cosx + isinx$
And I found a proof by using taylor series. So I am writting about it.

1. Tayolor series

테일러 급수란 어떤 f(x)가 있을 때 다음과 같은 식으로 나타내는 것을 말한다.

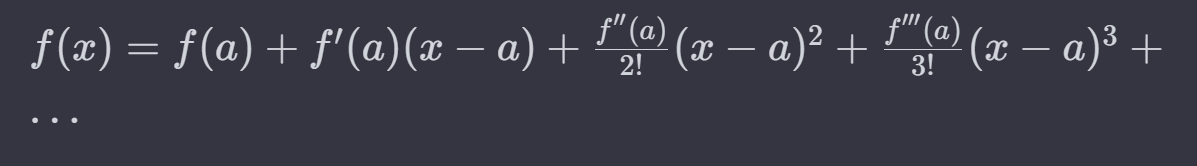
When you put a to this equation, each RHS and LHS has same value.
And if you differentiate both sides and put a, the equation is also same.

So I think Taylor series mimic the behavior of certain function by consisting itself of polynomial function has same derivatives.
In this taylor series above is 5th order. So, it has accuracy just as 5th order. When you increase the order, the accuracy will get better.

2. Proof of Euler's identity using Taylor series.

When x = 0, Taylor series is called Maclaurin series.
Maclaurin series of e^ix is as follows:

And Maclaurin series of i*sin(x) and cos(x) is like the followings.

When these two series is combined, it is same as the Maclaurin series of exponential.
However, I still can't understand. It is correct when x is around 0. It is not always true regardless of the value of x.

3. Application

Then why we use taylor series?
Because it converts some functions into the polynomial function that is easy to grasp. So we converts ln(x) or sin(X) or etc to get their values as shown below