[JS] 프로그래머스 - 표현 가능한 이진트리 해설포함 : 이진탐색 개념 정리

여러 코딩 테스트 문제를 풀다가 내가 이진탐색 구현을 완벽하게 정리한 적이 없어 조금 헷갈려한다는 사실을 깨달았다. 이 문제 뿐만 아니라 다양한 코딩테스트 문제 중에서도 이진탐색을 활용하여 시간복잡도를 단축하는 등 활용성이 높아 개념을 완벽하게 정리해 보고자한다.

이진탐색이 사용되는 경우

1. 정렬되어 있는 숫자 배열에서 해당 값 찾기

값이 정렬되어 있을 때 탐색하는 방법으로 시간복잡도를 O(n) 에서 O(logN) 으로 단축 시킬 수 있다.

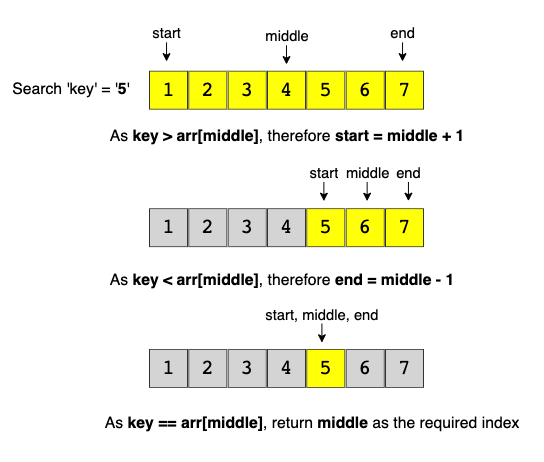
//while 문으로 구현한 이진탐색
function binarySearch(arr, target) {
  let left = 0;
  let right = arr.length - 1;
  
  while (left <= right) {
    const mid = Math.floor((left + right) / 2);
    if (arr[mid] === target) {
      return mid;
    } else if (arr[mid] < target) {
      left = mid + 1;
    } else {
      right = mid - 1;
    }
  }
  
  return -1;  // 찾는 요소가 배열에 없는 경우
}

//재귀함수 식으로 구현한 이진 탐색
function binarySearch(arr, target, left = 0, right = arr.length - 1) {
  if (left > right) {
    return -1;  // 찾는 요소가 배열에 없는 경우
  }
  
  const mid = Math.floor((left + right) / 2);
  if (arr[mid] === target) {
    return mid;
  } else if (arr[mid] < target) {
    return binarySearch(arr, target, mid + 1, right);
  } else {
    return binarySearch(arr, target, left, mid - 1);
  }
}

이진탐색을 구현할 때 까먹지 헷갈리지 말아야할 부분!

• 초기 left = 0, right = arr.length -1
• mid를 계산할 때에는 Math.floor((left+right)/2)
• 부분을 분할 할때 left = mid+1; right = mid - 1;
• 순회에 종료 조건은 left <= right 또는 left<right

2. 이진트리 탐색하기

카카오 코딩테스트: 표현가능한 이진트리
https://school.programmers.co.kr/learn/courses/30/lessons/150367

위에 문제를 풀기 위해 이진탐색을 활용했어야한다.

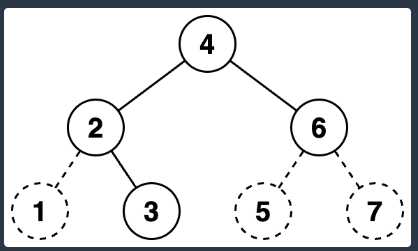
문제를 풀기 위한 로직

1. 십진수 수를 이진수 문자열 형태로 변환한다.
2. 포화 이진트리의 형태를 만족하기 위해 0 을 문자열 앞에 추가한다.

• 포화 이진트리의 형태는 일정 수에 노드 수를 만족해야한다.
• 높이가 3층인 이진트리라면 (2^3-1) 7개, 2진수 문자열 길이보다 크면서 가장 가까운 2^n-1를 찾고 문자열 길이가 2^n-1이 되도록 0을 추가하면 문제에서 설명하는 더미노드가 추가된 포화이진트리에 형태가 된다.

function solution(numbers) {
    const answer = [];
    for (let number of numbers) {
        //이진수 변환
        let bi_num = number.toString(2);
        let n = bi_num.length;
        //이진트리를 만들기 위한 노드 개수
        let m = n.toString(2).length
        // 이진수 앞에 0 추가
        let bi_tree = '0'.repeat(2**m-1 - n);
        bi_tree = bi_tree + '' + bi_num;
        if (checkBTree(bi_tree, 0, bi_tree.length-1)) {
            answer.push(1);
        }
        else {
            answer.push(0);
        }
    }
    return answer;
}

3. 이진수 문자열이 완성되면, 이 형태가 이진트리를 만족하는지를 봐야한다. (checkBTree 함수)

• 부모 요소가 0 일때, 자식 요소가 1이라면 이진트리 형태가 아니다.
• 그외 다른 형태는 이진트리라고 본다.

function checkBTree (b_str, start, end) {
    //부모 노드 idx
    const mid = Math.floor((start+end) / 2);
    //자식 노드 idx
    const left_c = Math.floor((start + mid-1)/2);
    const right_c = Math.floor((mid+1 + end)/2);
    
    //리프노드 도달
    if (start == end) {
        return true;
    }
    
    //부모가 0 인데 자식에 1이 있으면 안됨 -> 이 경우 false 를 반환
    if (b_str[mid] === '0' && ((b_str[left_c] === '1') || (b_str[right_c] === '1'))) {
        return false;
    }

    if (!checkBTree(b_str, start, mid-1)) return false;
    if (!checkBTree(b_str, mid+1, end)) return false;
    return true;
}

• 맨 처음 함수를 실행할 때는 start = 0, end = b_str.length-1로 두어 mid 가 정 가운데 루트노드를 찾을 수 있도록 한다.

• left_c right_c는 부모노드에서 뻗어나온 자식의 인덱스이자, 왼쪽 서브 트리와 오른쪽 서브 트리의 루트노드에 해당한다.

• start 와 end를 조정해가며 재귀적 호출을 통해 서브트리 검사를 시행한다.

• b_str[mid] 가 0 인데, b_str[left_c], b_str[right_c] 중 1이 있으면 false를 반환하여 함수 호출을 중단한다.

• start 와 end가 같아지면 더 이상 자식 노드가 없는 리프노드에 도달했다는 의미임으로 true를 반환하여 함수 호출을 중단한다.

• 재귀 함수 호출을 if 문으로 감싸 반환되는 값의 t/f 에 따라 최종 return 값을 달리하여, 불필요한 콜 스택이 쌓이는 것을 막을 수 있었다.