• 알고리즘 분석
  알고리즘의 자원(resource) 사용량을 분석
  자원이란 시간 메모리 등을 말함.

시간 복잡도 Time Complexity

• 프로그램의 실행시간은 실행환경에 따라 달라짐.
• 특정 크기의 입력에 대해 알고리즘이 얼마나 오래 걸리는지에 대해 해당 알고리즘이 걸리는 시간.
• 실행 시간을 측정하는 대신 연산 실행 횟수를 셈.
• 데이터의 크기가 같더라도 실제 데이터에 따라 계산 횟수가 달라질 수 있다.

• 데이터의 크기가 같더라도 실제 데이터에 따라 계산 횟수가 달라질 수 있음.
• O (Big - 오), 상한
  O(g(n))은 g(n)이라는 함수보다 증가율이 같거나 더 느린 함수들의 집합이다.
• big-Ω (Big - 오메가), 하한
  g(n)이라는 함수보다 증가율이 더 같거나 더 빠른 함수들의 집합이다.오메가
• θ (Big - 세타)
  g(n)이라는 함수랑 증가율이 같은 함수들의 집합
  가장 쓸모있는 개념.

• 근데 실제로는 big-O만 쓰는데?
  실제 업계에서는 big-O를 big-θ처럼 쓴다.
• 알고리즘 수행 시간을 따질 때 경우에 따라 다른 시간 복잡도가 나올 수 있다.
  이중 최선의 시간보다는 평균적인 경우, 혹은 최악의 경우를 주로 고려한다.

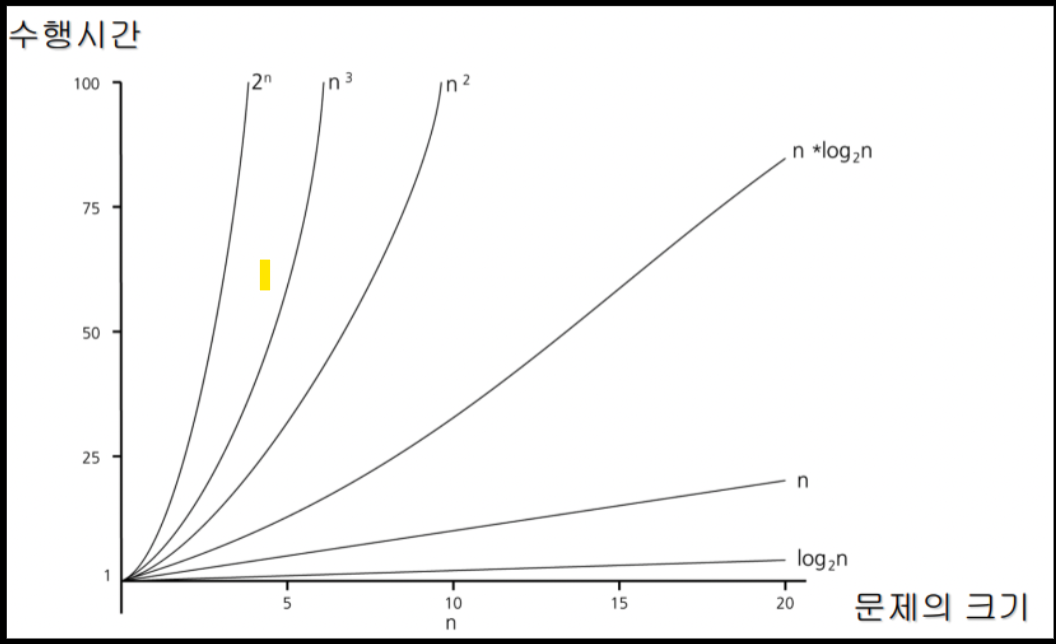
점근적 분석

• 알고리즘의 성능은 입력의 크기가 충분히 클 때의 성능이 중요하다.
  알고리즘의 수행 시간은 항상 입ㄺ의 크기가 충분히 클 때를 분석한다.

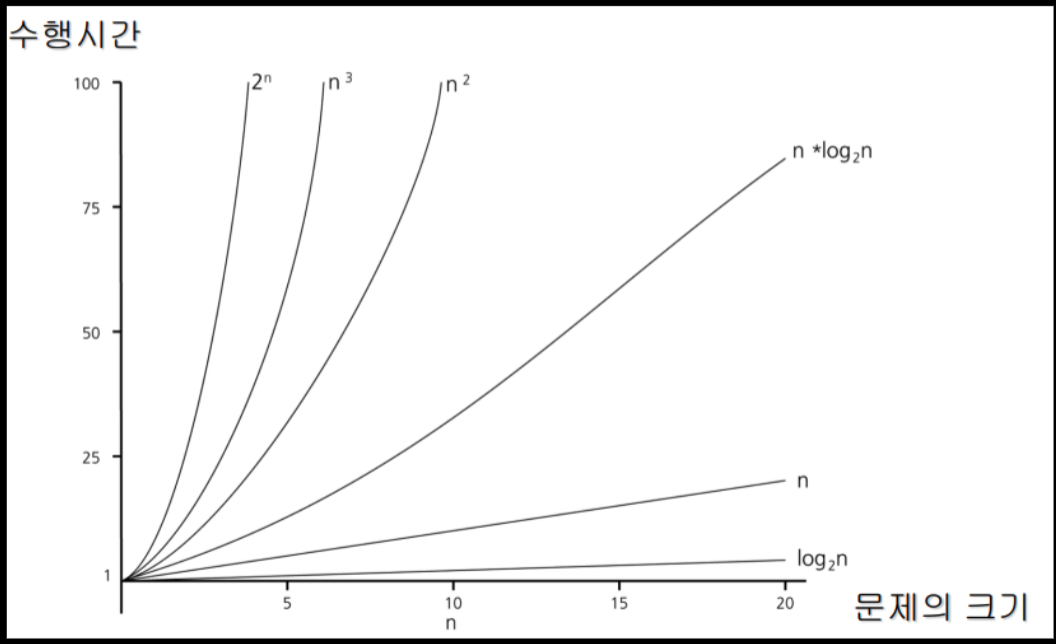
• Asymptotic notation (점근적 분석)
  시간 제한이 1초일 때. 적절한 시간 복잡도
  N 500이하 정도 -> O(n^3)
  N 2000 이하 -> O(n^2)
  N 100000 (십만) 이하 -> O(NlogN)
  N 10000000 (천만) -> O(N)
• 인풋이 작다. -> 반복으로 탐색해도 좋다. 완전탐색.
  인풋이 크다. -> 시간복잡도를 고려해야한다.

공간복잡도

• 특정한 크기의 입력에 대해 알고리즘이 얼마나 많은 메모리를 차지하는지를 의미.

메모리의 양

• 공간 복잡도 또한 빅-O 표기법 이용
• 일반적으로 메모리 사용량 기준은 MB단위로 표기한다.
  일반적으로 리스트의 크기가 100만개 이상의 데이터를 선언하는 경우는 매우 적을 것이다.

• 인풋이 너무 크면 의심해보자

슬라이딩 윈도우 Sliding Window

배열이나 리스트의 요소의 일정 범위의 값을 비교할 때 사용.

투포인터

자유롭게 두 값을 지정해서 연산.

재귀 알고리즘

1. 재귀 알고리즘은 베이스 케이스(재귀 호출을 유발하지 않는 종료 시나리오)가 있어야 함.
2. 재귀 알고리즘은 상태를 변경하고 베이스 케이스로 이동한다.
3. 재귀 알고리즘은 재귀적으로 자신을 호출.
   재귀 알고리즘은 최소 O(n)의 공간을 사용. 여기서 n은 재귀 호출의 깊이.