비선형 자료구조 - Graph

그래프 Graph

정점과 간선으로 이루어진 자료구조 (Cyclic)

• 연결된 정점간의 관계를 표현할 수 있는 자료구조
• 용도 : 지하철의 노선도, 통신 네트워크, ...

그래프 구조

정점(Vertex) : 각 노드	간섭(Edge) : 노드와 노드를 연결하는 선 (link, branch)
인점정점(Adjacent vertext) : 간선 하나를 두고 바로 연결된 정점	정점의 차수 (Degree) : - 무방향 그래프에서 하나의 정점에 인접한 정점의 수 - 무방향 그래프 모든 정점 차수의 합 = 그래프 간선의 2배
진입 차수 (In-degree) : 방향 그래프에서 외부에서 오는 간선의 수	진출 차수 (Out-degree) : 방향 그래프에서 외부로 나가는 간선의 수
경로 길이 (Path length) : 경로를 구성하는데 사용된 간선의 수	단순 경로 (Simple path) : 경로 중에서 반복되는 정점이 없는 경우
사이클 (Cycle) : 단순 경로의 시작 정점과 끝 정점이 동일한 경우

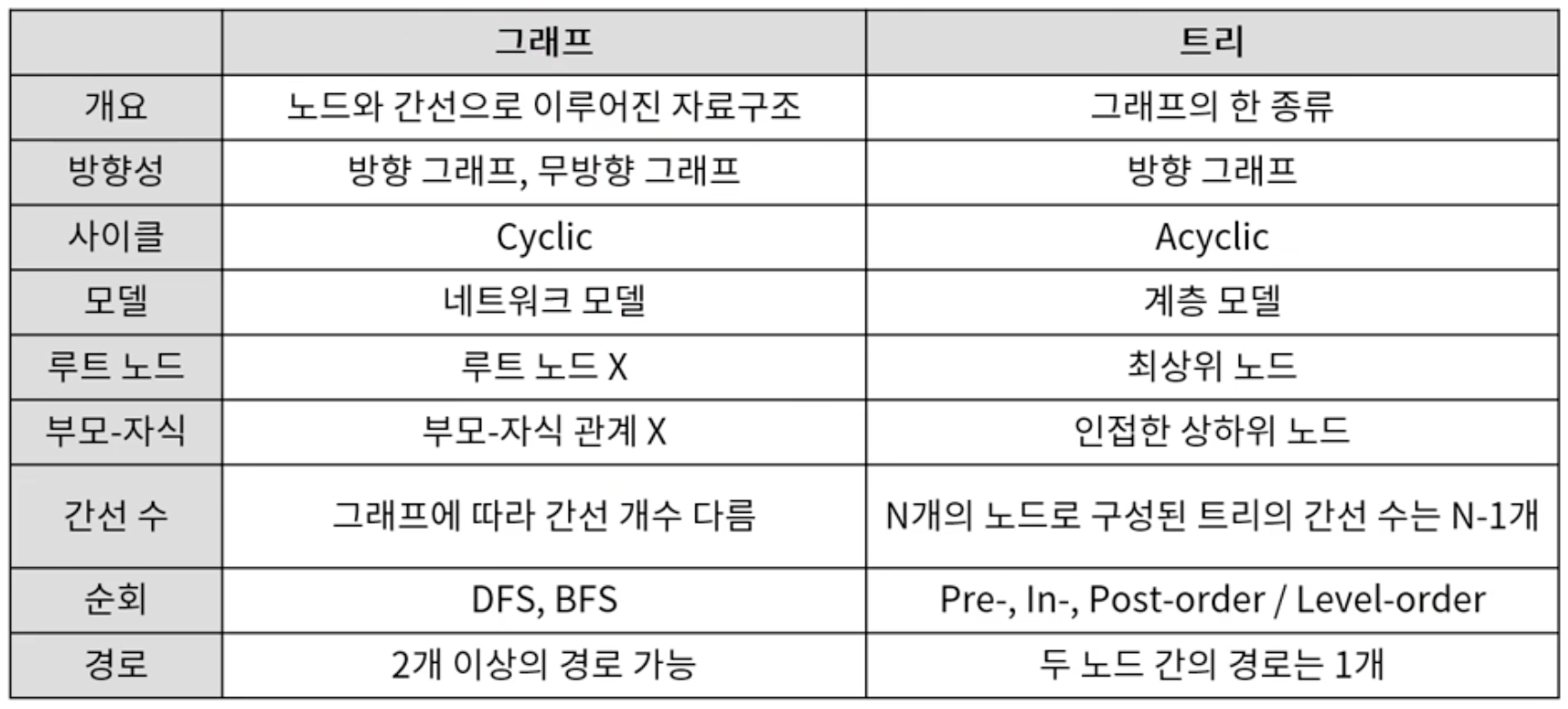
그래프의 특징과 트리와의 차이

그래프의 종류

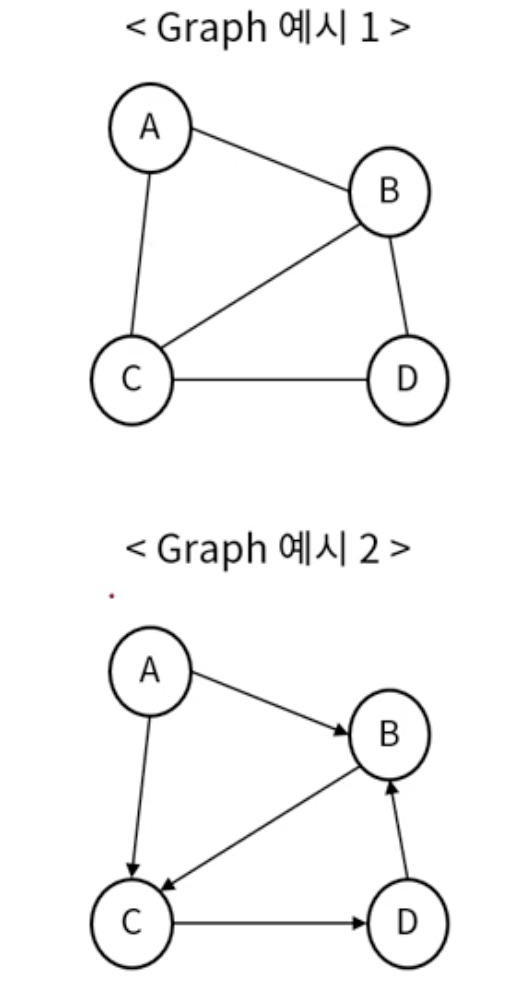
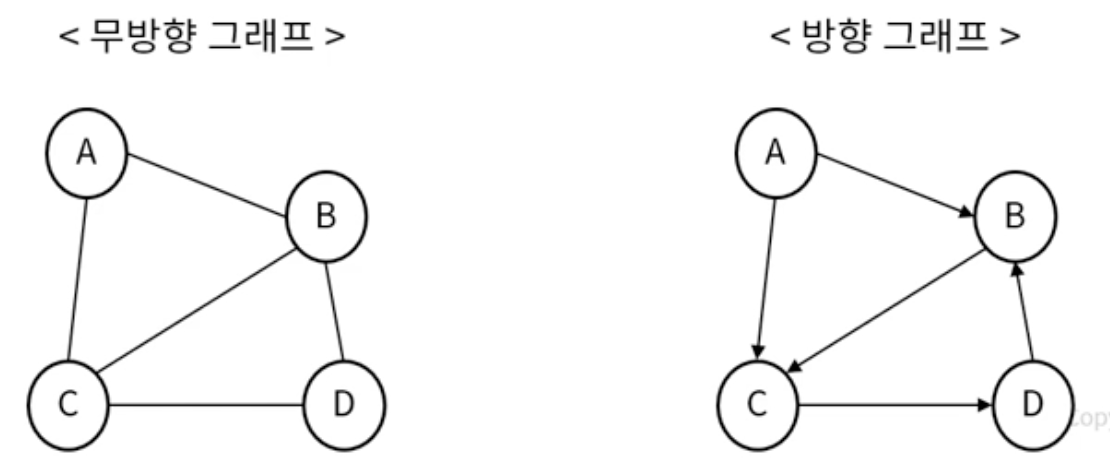
무방향 그래프

• 간선에 방향이 없는 그래프 (양방향 이동 가능)
• 정ㅈ머 A - B 간선의 표현 : (A, B) = (B, A)

방향 그래프

• 간선에 방향이 있는 그래프 (해당 방향으로 이동 가능)
• 정점 A -> B 간선의 표현 : <A, B> != <B, A)

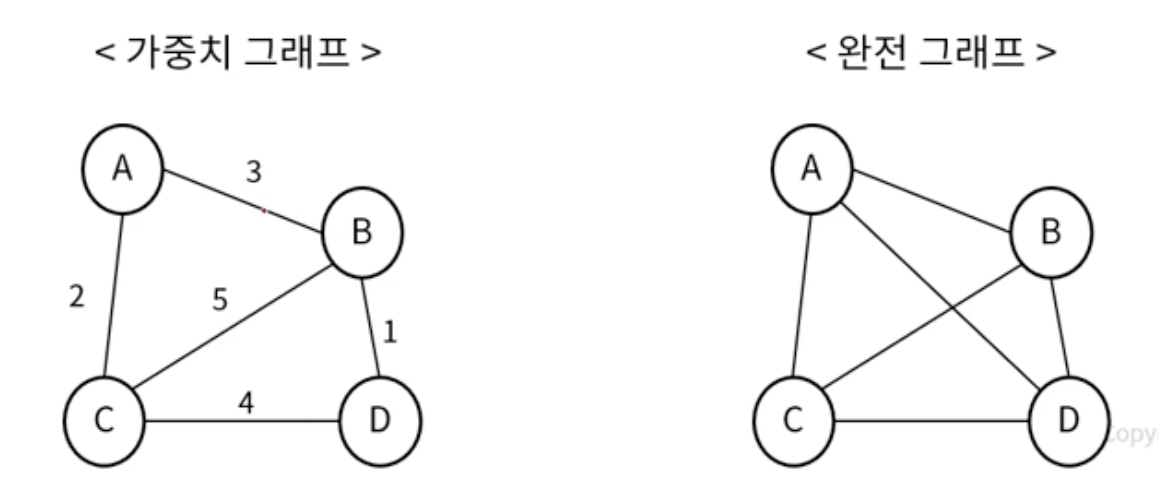
가중치 그래프

• 간선에 값이 있는 그래프 (이동 비용)

완전 그래프

• 모든 정점이 서로 연결되어 있는 그래프
• 정점이 N개일 경우, 간선의 수는 n(n-1) / 2개

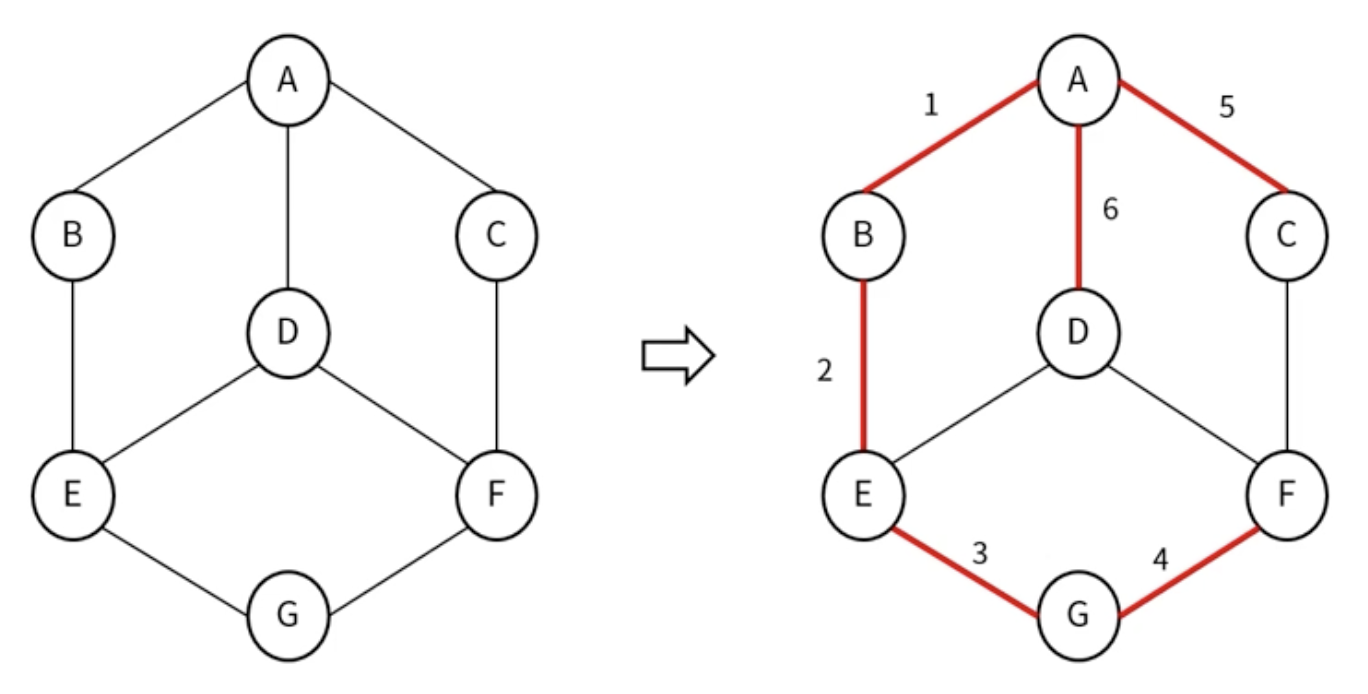
그래프 탐색 - DFS

깊이 우선 탐색 (Depth First Search)

각 노드에 방문했는지 여부를 체크할 배열과 스택을 이용하여 구현

그래프 탐색 - BFS

너비 우선 탐색 (Breath First Search)

각 노드에 방문했는지 여부를 체크할 배열과 큐를 이용하여 구현

그래프의 구현

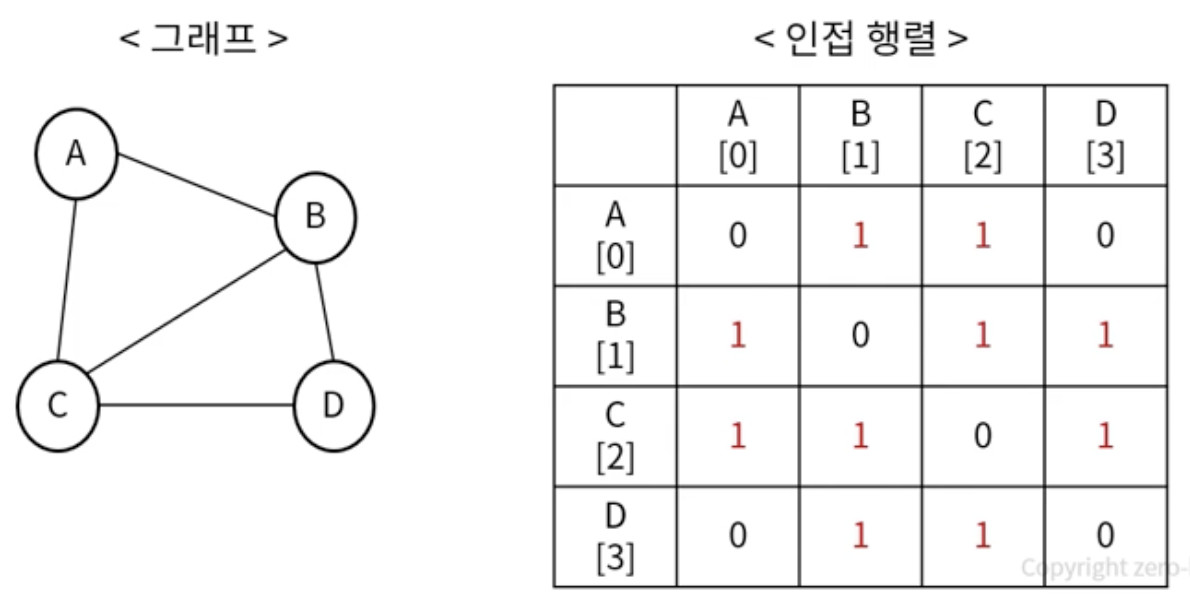
인접 행렬 (Adjacency Matrix) - 2차원 배열 이용

• 인접 행렬의 장단점
  • 간섭 정보의 확인과 업데이트가 빠름 O(1)
  • 인접 행렬을 위한 메모리 공간 차지

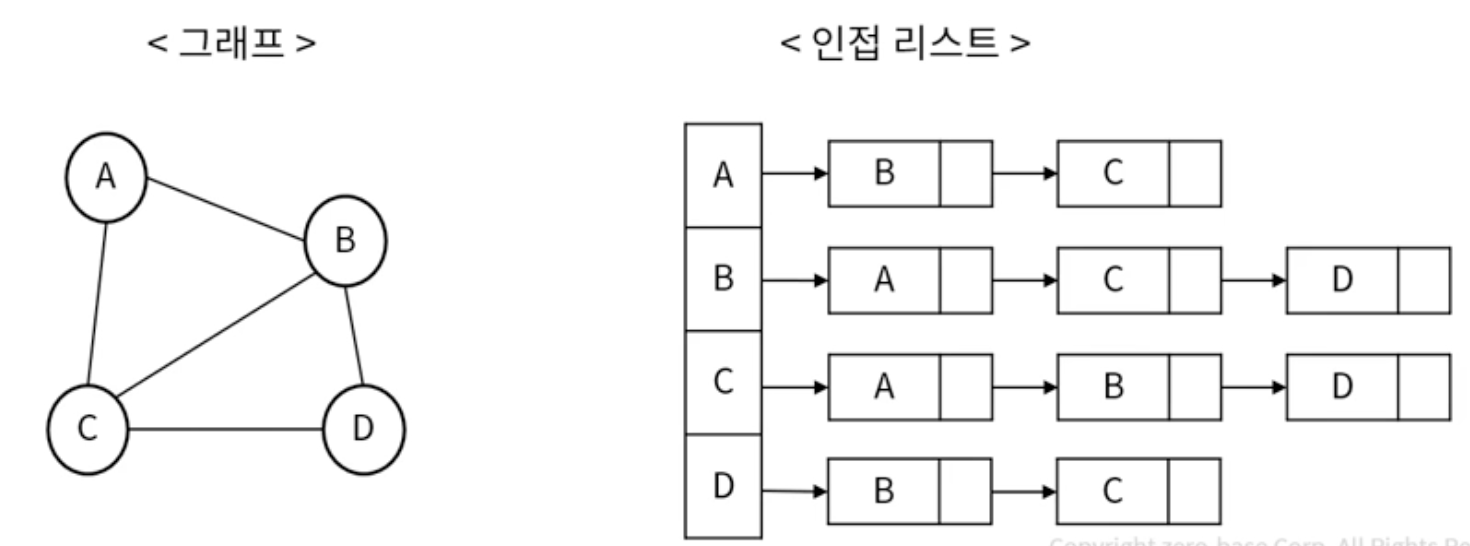
인접 리스트 (Adjacency List) - 연결리스트 이용

• 인접 리스트의 장단점
  • 메모리 사용량이 상대적으로 적고, 노드의 추가 삭제가 빠름
  • 간선 정보 확인이 상대적으로 오래 걸림