프로그래머스 광고삽입 파이썬 풀이

2021 KAKAO BLIND RECRUITMENT 광고 삽입 링크

유형

• 누적합
• 배열에 중첩해서 범위 표시하는데 for문으로하면 시간초과나는 문제

이전에 풀었던 파괴되지 않는 건물 문제와 비슷하게 누적합 원리를 이용하면 쉽다.
이 문제를 풀어보기 전에 먼저 파괴되지 않는 건물을 풀어보는 것을 추천한다.

• 파괴되지 않는 건물 풀이

파괴되지 않는 건물 문제가 누적합을 2차원에서 응용하는 문제였다면 이 문제는 timetable 위에서 응용하는 문제다.

말로는 어렵고 그림으로 보면 이해가 쉬워서 파워포인트로 그려봤다.

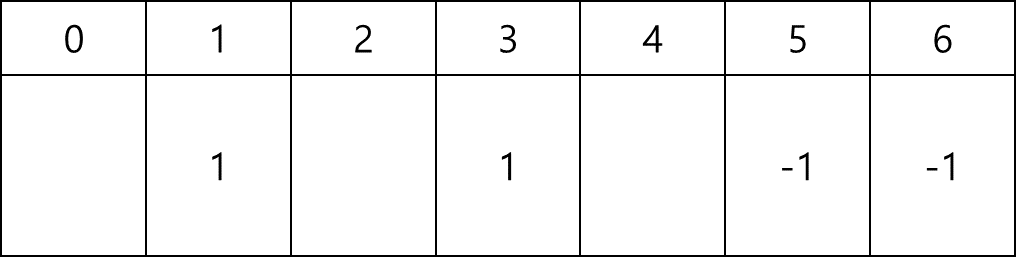
우선 배열에 표시를 해놔야 한다. 각 시청자마다 시청 시작할때는 1, 끝날 때는 -1을 더해준다.

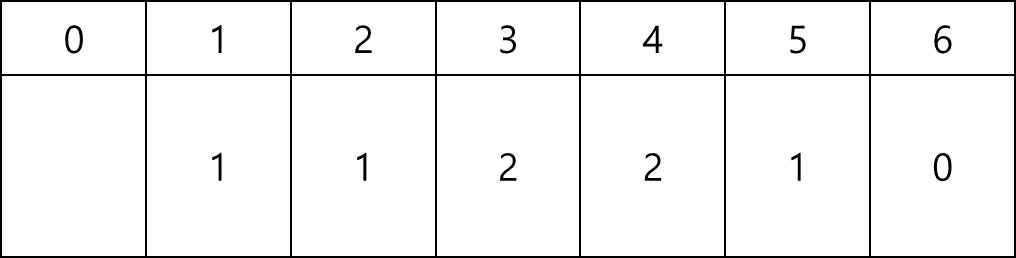
이 배열을 누적합 모양으로 만들어주면 각 시간에서의 시청자 수를 알 수 있다.
이제 이 배열의 구간 합이 최대가 되는 구간을 찾으면 정답이다.

그래서 sum으로 구간의 합을 구하면 답이 되는걸까?
아니다.

누적 합은 원래 구간 합을 상수 시간에 접근하고 싶을 때 사용한다는 것을 잊지말자.
[a, b) 구간의 합 = pre_sum[b-1] - pre_sum[a-1]

이제 이걸로 최대가 되는 구간만 구하면 된다.

파이썬 코드

def time_to_sec(time):
    h, m, s = map(int, time.split(':'))
    return h * 60 * 60 + m * 60 + s

def sec_to_time(sec):
    h, m, s = sec // 3600, sec % 3600 // 60, sec % 60
    return f'{h:02}:{m:02}:{s:02}'

def solution(play_time, adv_time, logs):
    play = time_to_sec(play_time)
    adv = time_to_sec(adv_time)

    viewers = [0 for _ in range(100 * 60 * 60 + 1)]

    for log in logs:
        start, end = map(time_to_sec, log.split('-'))
        viewers[start] += 1
        viewers[end] -= 1
        
    p = 0
    viewers[1] += 2*viewers[0]
    for i in range(2, len(viewers)):
        viewers[i] += 2*viewers[i-1] -viewers[i-2] 
		# viewers[i-1] + viewers[i-1] - viewers[i-2]
        
    
    # t == 0
    mx = viewers[adv]
    answer = 0
    
    for t in range(1, play-adv+1):
        view = viewers[t + adv-1] - viewers[t - 1]
        if view > mx:
            mx = view
            answer = t
        
    return sec_to_time(answer)

참고 사항

• 누적 합에서 [a, b]의 구간 합을 구할 때 p_sum[b] - p_sum[a-1]이 생각나지 않는다면 쓸 수 있는 방법이 있다.
  • arr 배열을 prefix_sum으로 만든 p_sum이 있다.
  • arr[i] = p_sum[i] - p_sum[i-1]
  • arr[i] + arr[i+1] = p_sum[i] - p_sum[i-1] + p_sum[i+1] - p_sum[i]
  • arr[i] + arr[i+1] = p_sum[i+1] - p_sum[i-1]]
  • i, i+1을 a, b로 바꾸면
  • arr[a] + arr[b] = p_sum[b] - p_sum[a-1]
  • 엄밀히 맞지는 않지만 이거 생각하면 바로 기억난다.
• 코드에서는 누적합을 두 번 진행하지 않고 식을 계산하여 한 번에 진행했다.
• 이 문제에서 시청자 재생시간은 [a, b), a 이상 b 미만으로 구한다.
  이거 주의해야 한다. 다 풀어놓고 틀릴 수 있다.