하노이의 탑 (Lv.2) 문제 링크
하노이의 탑 문제는 수학이나 알고리즘에서 유명한 문제입니다.
먼저 이 문제를 풀기 위해서는 하노이의 탑 룰에 대한 이해가 필요합니다.
1~N번 원판을 C로 옮기는 과정을 다음과 같은 세 단계로 나눌 수 있습니다.
- 1~N-1번 원판을 A에서 B로 이동
- N번 원판을 A에서 C로 이동
- 1~N-1번 원판을 B에서 C로 이동
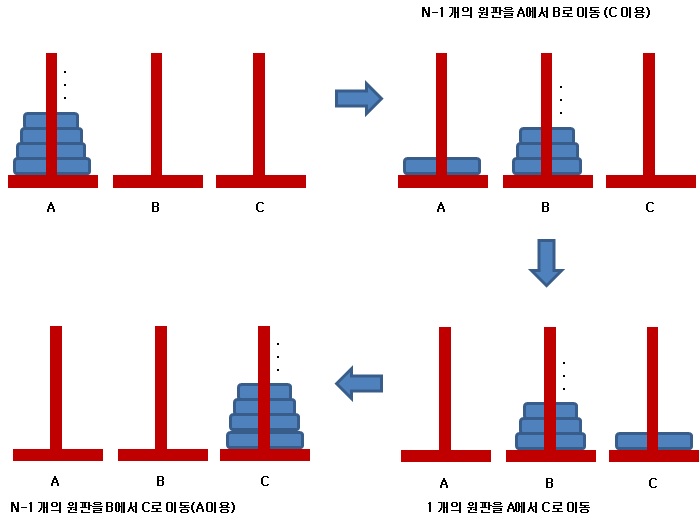 이미지 출처: https://ehclub.co.kr/1238
이미지 출처: https://ehclub.co.kr/1238
풀이
- 1~N-1번 원판을 A에서 B로 이동
- N번 원판을 A에서 C로 이동
- 1~N-1번 원판을 B에서 C로 이동
기본적으로 이 세 단계를 각 원판에 적용하는 것이 목표지만, 가장 위에 있는 원판은 경유하지 않고 목적지로 옮기면 된다.
코드
def get_hanoi(n, start, via, dest):
if n == 0:
return []
# via = [x for x in [1, 2, 3] if x != start and x != dest][0]
return get_hanoi(n-1, start, via) + [[start, dest]] + get_hanoi(n-1, via, dest)
def solution(n):
return get_hanoi(n, 1, 2, 3)- start, via, dest는 순서대로 출발지, 경유지, 목적지입니다.
- get_hanoi 함수가 항상 리스트를 반환하므로 + 연산자를 이용해 간단하게 표시할 수 있습니다.
- n이 1인 경우를 마지막으로 하도록 탈출 조건을 설정해야 한다.

