📌 이진 탐색 트리(Binary Search Tree, BST)란?

이진 탐색 트리(Binary Search Tree, BST)는 트리 구조의 일종으로, 각 노드가 하나의 값과 두 개의 자식 노드(왼쪽 자식과 오른쪽 자식)를 가지는 구조입니다. 이진 탐색 트리의 특징은 각 노드의 왼쪽 자식 노드는 해당 노드의 값보다 작고, 오른쪽 자식 노드는 해당 노드의 값보다 크다는 규칙을 따릅니다.

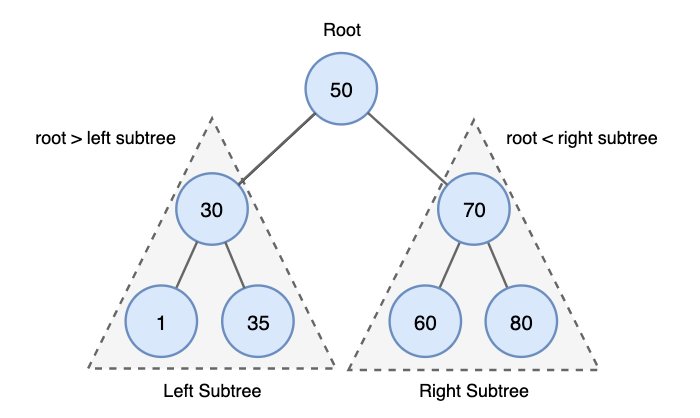
특징

• 각 노드의 자식이 2개 이하
• 각 노드의 왼쪽 자식은 부모보다 작고, 오른쪽 자식은 부모보다 큼
• 중복된 노드가 없어야 함
• 이진탐색트리의 순회는 '중위순회(inorder)' 방식 (왼쪽 - 루트 - 오른쪽)

시간 복잡도

최선의 경우 (균형 상태 트리)
탐색 (Search): O(log n)
삽입 (Insertion): O(log n)
삭제 (Deletion): O(log n)

최악의 경우 (한 쪽으로 치우친 트리)
탐색 (Search): O(n)
삽입 (Insertion): O(n)
삭제 (Deletion): O(n)

삭제의 3가지 Case

자식이 없는 leaf 노드일 때 → 그냥 삭제

자식이 1개인 노드일 때 → 지워진 노드에 자식을 올리기

자식이 2개인 노드일 때 → 오른쪽 자식 노드에서 가장 작은 값 or 왼쪽 자식 노드에서 가장 큰 값 올리기

📌 연산

검색

1. 루트에서 시작합니다.
2. 검색 값을 루트와 비교합니다. 루트보다 작으면 왼쪽에 대해 재귀하고 크다면 오른쪽으로 재귀합니다.
3. 일치하는 값을 찾을 때까지 절차를 반복합니다.
4. 검색 값이 없으면 null을 반환합니다.

삽입

1. Root에서 시작합니다.
2. 삽입 값을 루트와 비교합니다. 루트보다 작으면 왼쪽으로 재귀하고 크다면 오른쪽으로 재귀합니다.
3. 리프 노드에 도달한 후 노드보다 크다면 오른쪽에 작다면 왼쪽에 삽입합니다.

삭제

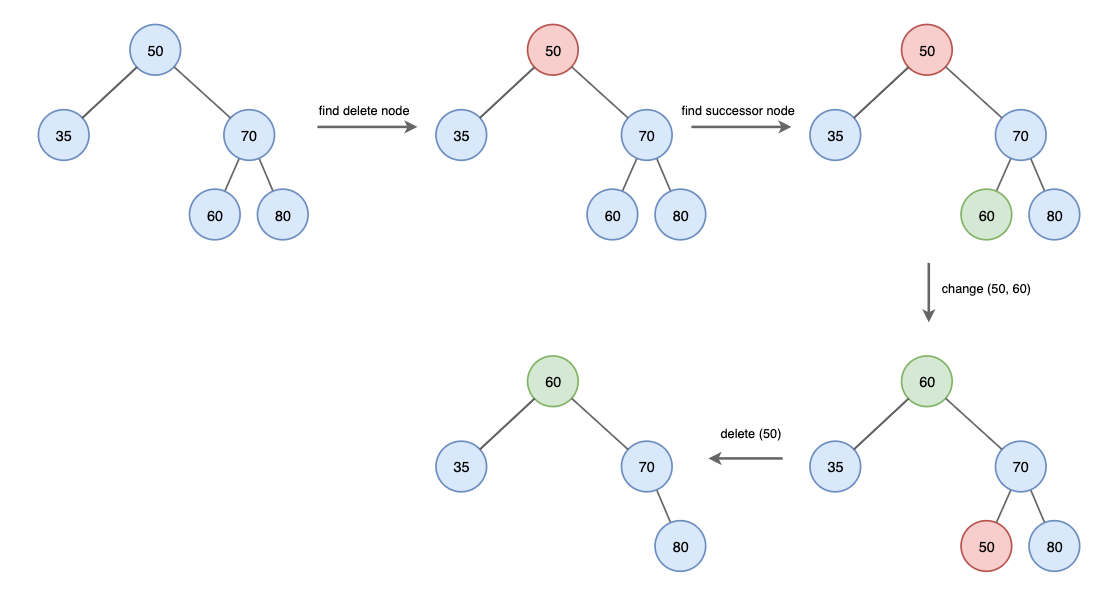
successor 노드란

right subtree에 최소값
즉, inorder 순회에서 다음 노드를 말합니다.

1. 삭제할 노드를 찾습니다.
2. 삭제할 노드의 successor 노드를 찾습니다.
3. 삭제할 노드와 successor 노드의 값을 바꿉니다.
4. successor 노드를 삭제합니다.

참고

• https://gyoogle.dev/blog/computer-science/data-structure/Binary%20Search%20Tree.html
• https://yoongrammer.tistory.com/71

피드백 및 개선점은 댓글을 통해 알려주세요😊