🍀 버블 정렬(bubble sort)

버블 정렬은 가장 간단하면서 기본적인 정렬 방식으로서 정렬을 공부할 때 맨 처음에 접하는 정렬 방식이다. 버블 정렬은 바로 앞, 뒤의 요소를 비교하고 swap 하는 방식으로 정렬을 진행하며 오름차순 정렬이라고 가정할 시 가장 큰 요소가 제일 먼저 정렬 되는 특징이 있다. 또한 정렬이 되어 있지 않은 상태에서 정렬을 진행한다면 O(N^2) 의 시간 복잡도를 가지고 있어 특정한 상황을 제외하고선 버블 정렬이 거의 쓰이지 않는다고 한다. 하지만, 버블 정렬을 시작으로 다른 정렬 알고리즘을 터득하기 위한 밑거름이 되리라 믿는다.

Pseudo Code

• 1️⃣ for ⇒ i가 배열 길이 - 1까지
  • 2️⃣ for ⇒ j가 배열 길이 - 1 - i까지
    • 3️⃣ if ⇒ j에 위치한 요소 > j + 1에 위치한 요소 → swap

💡 3️⃣ 의 이유 때문에 버블 정렬을 교환 기반 알고리즘이라고 한다.

그래도 그림이 의사 코드 보다는 시각적이기 때문에 figma를 이용하여 그림 좀 그려봤다.

[5, 3, 4, 1, 2] 라는 배열이 있다고 가정하면 버블 정렬이 일어나는 과정은 아래와 같다.(편의상 1️⃣의 루프가 돌 때 2️⃣번의 루프는 동일한 동작을 하므로 한 번의 정렬만 시각화 했다.)

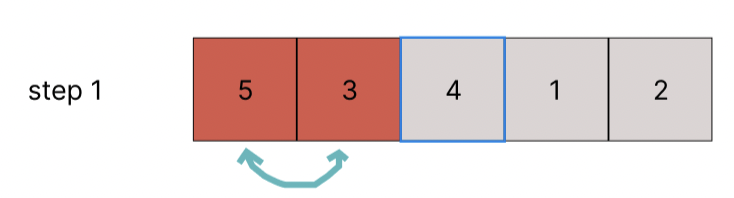
5 > 3이므로 swap한다.

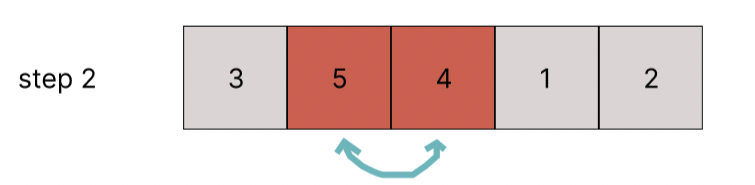
5 > 4이므로 swap한다.

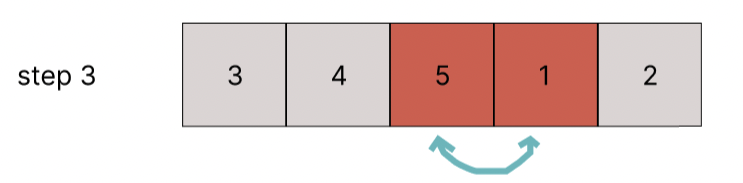
5 > 1 이므로 swap한다.

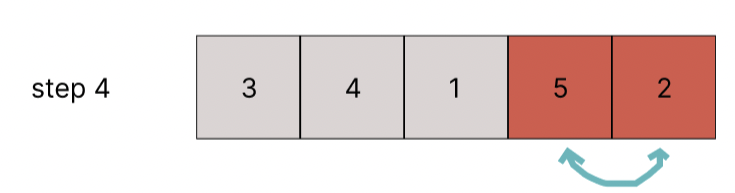
5 > 2 이므로 swap한다.
이제 내부 for 루프가 끝났으므로 한 번 정렬한 결과는 아래와 같다.

이렇게 위와 같이 1️⃣의 for loop가 끝날 때까지 앞, 뒤 요소를 비교하고 swap을 진행하면 [1, 2, 3, 4, 5] 로 정렬됨을 알 수 있다.

구현

먼저 테스트 해볼 배열을 생성해줄 함수를 만들고

const createArr = (arrLength, maxNum) => {
  if (arrLength > maxNum) {
    throw Error('max number should be bigger than array length!')
  }

  const result = [];

  for (let i = 0; i < arrLength; i++) {
    let randomNum = Math.floor(Math.random() * maxNum);
    while (result.includes(randomNum)) {
      randomNum = Math.floor(Math.random() * maxNum);
    }
    result.push(randomNum);
  }

  return result;
};

pseudo code에 맞게 bubble sorting해줄 함수를 만들면 아래와 같다.

const bubbleSort = (arr, reverse = false) => {
  const sortedArr = [...arr];
  console.log('정렬 중... ', sortedArr)
  for (let i = 0; i < arr.length - 1; i++) { // 👉🏻 pseudo code 1️⃣
    for (let j = 0; j < arr.length - 1 - i; j++) { // 👉🏻 pseudo code 2️⃣
      if (sortedArr[j] > sortedArr[j + 1]) { // 👉🏻 pseudo code 3️⃣
        [sortedArr[j], sortedArr[j + 1]] = [sortedArr[j + 1], sortedArr[j]];
      }
      console.log('정렬 중... ', sortedArr)
    }
    console.log(`\n${"=".repeat(30)}`);
    
  }

  return sortedArr;
};

위에서 만든 두 함수를 아래 코드를 통해서 테스트 해보면

const arr = createArr(5, 5);
console.log('버블정렬 전 👉🏻', arr);
console.log(`\n${"=".repeat(30)}`);
const sortedArrByBubbleSort = bubbleSort(arr);
console.log('버블정렬 후 👉🏻', sortedArrByBubbleSort);

위와 같은 결과를 터미널에서 확인해 볼 수 있다. 그리고 빨간줄 라인의 빨간색 동그라미를 보면 가장 큰 수가 가장 먼저 정렬이 됨을 확인해 볼 수 있다.

위는 오름차순 기반으로 작성한 것이며 내림차순으로 만들고 싶다면, 오름차순과 내림차순에 관련된 변수 reverse(true -> 오름차순, false -> 내림차순) 를 만들자

난 reverse에 따라 swap할 조건이 바뀔 수 있으므로 bubbleSort안에 내부 함수인 getCondition함수를 작성했다. 그리고 reverse값을 true로 주면 잘 작동함을 볼 수 있다.

const bubbleSort = (arr, reverse = false) => {
	const getCondition = (num1, num2, reverse) => {
    return reverse ? num1 < num2 : num1 > num2;
  }

	...//
		for (let j = 0; j < arr.length - 1 - i; j++) {
      if (getCondition(sortedArr[j], sortedArr[j + 1], reverse)){
        [sortedArr[j], sortedArr[j + 1]] = [sortedArr[j + 1], sortedArr[j]];
      }
      console.log('정렬 중... ', sortedArr)
    }
	...//
}

...//
const sortedArrByBubbleSort = bubbleSort(arr, reverse = true);
...//

내림차순으로 정렬 했으므로 가장 작은 값이 제일 먼저 정렬됨을 확인할 수 있다.

🛠️ 최적화

만약에 배열이 거의 정렬되어있다고 한다면 O(N) 의 시간 복잡도를 가진다고 한다. 위에서 분명 for loop를 두 번 사용했는데 어떻게 O(N)의 시간 복잡도를 가진다고 할 수 있을까???
생각해 보면, 내부 for 구문을 한 번 돌았을 때 swap이 한 번도 일어나지 않는다면 이미 정렬이 되어 있는 상태이므로 정렬을 멈추면 된다. 이렇게 하게 되면 O(N)의 시간 복잡도를 가질 수 있다. 구현은 매우 간단한데 swap이 일어났는지에 대한 유무인 isSwapped 변수를 이용할 것이다.

const bubbleSort = (arr, reverse = false) => {
  ...//
  for (let i = 0; i < arr.length - 1; i++) {
    let isSwapped = false; // 🛠️

    for (let j = 0; j < arr.length - 1 - i; j++) {
      if (getCondition(sortedArr[j], sortedArr[j + 1], reverse)){
        [sortedArr[j], sortedArr[j + 1]] = [sortedArr[j + 1], sortedArr[j]];
        isSwapped = true; // 🛠️ swap이 일어났다면 isSwapped 플래그를 true로 설정
      }
      console.log('정렬 중... ', sortedArr)
    }
    
    if (!isSwapped) break; // 🛠️
  }
	...//
};

위와 같이 구현을 하면 만약 정렬되어 있는 상태라면 O(N) 의 시간 복잡도를 가질 것이다.

버블 정렬에 대해서 간단히 정리하면

• 시간 복잡도
  • 정렬이 안 되어있을 때(최악) ⇒ O(N^2)
  • 정렬이 되어 있을 때(최선) ⇒ O(N)
• 오름차순 정렬일 시 가장 큰 값이 먼저 정렬(내림차순은 반대)
• 앞, 뒤 값을 비교 후 swap함으로 교환 기반 알고리즘 이라 할 수 있다.
• 정렬을 할 때 추가적인 메모리 공간 소요가 없음.
• 퍼포먼스는 다른 정렬 알고리즘에 비해서 상당히 낮다.

🔥 마치며

사실상 정렬에 대한 것은 예전에 공부해봤지만 구현한 기억은 없다. 그리고 이게 이 정렬이었나?? 명칭이 다소 헷갈려 한 번 정리한 김에 정렬에 관한 것을 구현까지 한 번 정리 해 보려고 한다. 확실히 구현을 해 보면 머릿속에 잘 남는다. 그리고 알고리즘 공부를 하면서 구현 실력이 늘어서 그런가 바로 구현할 수 있어서 좋았다. 버블 정렬은 퍼포먼스가 너무 떨어지기 때문에 이보다 더 좋은 정렬 알고리즘들이 있다. 이 다음에는 삽입, 선택 정렬에 대해서 정리해보려고 한다. 그런데 정렬된 배열인 경우 버블 정렬의 시간 복잡도가 O(N^2)이라고 하는데....;; 난 아무리 봐도 O(N)인 것 같다....;; 이건 더 알아봐야 할 것 같다.