🍀 삽입 정렬(insertion sort)

삽입정렬은 정렬할 영역을 점진적으로 증가시키면서 정렬할 영역 내에 요소를 올바른 위치에 삽입 하여 정렬하는 방식이다. 삽입 정렬 또한 버블, 선택 정렬과 마찬가지로 최악의 경우(정렬이 되어 있지 않을 경우) O(N^2)을 가지지만 최선의 경우(정렬이 정렬되어 있을 때) 버블정렬과 마찬가지로 O(N)의 시간 복잡도를 가진다. 삽입 정렬 또한 다른 정렬 블로그와 마찬가지로 오름차순 정렬기반으로 작성했다.

Pseudo Code

• 1️⃣ for ⇒ i가 1부터 배열 길이까지
  • 2️⃣ for ⇒ j가 i - 1부터 0까지
    • 3️⃣ if ⇒ j 위치의 요소 > j + 1위치의 요소 → swap

🌊 삽입 정렬 시각화

삽입 정렬은 한 예만 보여주는 것 보다는 크게크게 시각화를 하는 것 같아서 내부 for 루프가 끝나는 시점을 기반으로 시각화를 했다.
정렬 전 배열을 [5, 3, 4, 1, 2] 라고 하고 삽입할 영역(j가 도는 구간)을 초록색으로 표시하고, 삽입할 값(i에 위치한 값)을 빨간색으로 표시했다.

초록색 구간에 있는 값은 3 하나 밖에 없으며 4는 초록색 영역 중에 삽입할 곳이 존재하지 않으므로 다음 step으로 넘어간다.

빨간색에 해당하는 값인 1은 3과 4보다 앞에 위치하므로 맨 앞에다가 삽입한다.

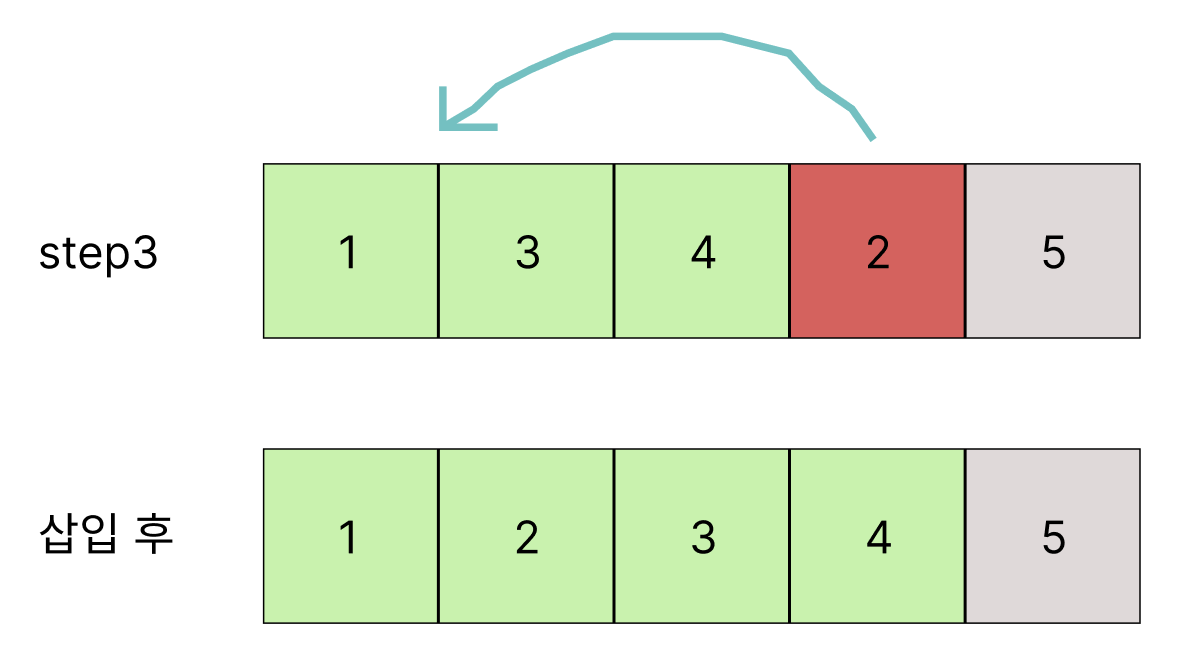
삽입할 값인 빨간색 값 2는 1보다 크고 3보다 작으므로 그 사이에 삽입한다.

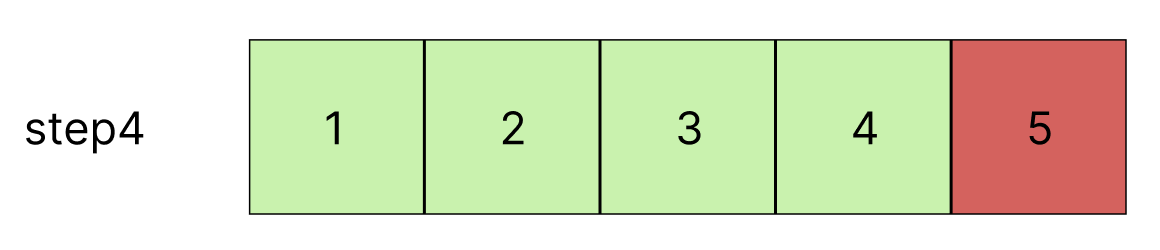
5는 초록색영역의 숫자들보다 크므로 삽입이 일어나지 않는다.
이렇게 모든 정렬이 끝나게 된다.

구현

createArr, getCondition, swap 함수는 버블 정렬을 정리할 때 올린 곳에 있다. 구현 또한 통으로 올렸다.

const createArr = (arrLength, maxNum) => {
  if (arrLength > maxNum) {
    throw Error('max number should be bigger than array length!')
  }

  const result = [];

  for (let i = 0; i < arrLength; i++) {
    let randomNum = Math.floor(Math.random() * maxNum);
    while (result.includes(randomNum)) {
      randomNum = Math.floor(Math.random() * maxNum);
    }
    result.push(randomNum);
  }

  return result;
};


const inserstionSort = (arr, reverse = false) => {
  const getCondition = (num1, num2, reverse) => {
    return reverse ? num1 < num2 : num1 > num2;
  };

  const swap = (arr, idx1, idx2) => {
    [arr[idx1], arr[idx2]] = [arr[idx2], arr[idx1]];
  };

  const sortedArr = [...arr];

  for (let i = 1; i < arr.length; i++){  // 👉🏻 1️⃣
    let j = i - 1;

    while (j >= 0){ // 👉🏻 2️⃣
      if (getCondition(sortedArr[j], sortedArr[j + 1], reverse)) swap(sortedArr, j, j + 1);
      j -= 1;
    }

    console.log('정렬 중...', sortedArr);
    console.log('='.repeat(30));
  }

  return sortedArr;
}

const arr = createArr(5, 5);
console.log("삽입 정렬 전 👉🏻", arr);
console.log(`\n${"=".repeat(30)}`);
const sortedArrByInsertionSort = inserstionSort(arr, (reverse = false));
console.log("\n삽입 정렬 후 👉🏻", sortedArrByInsertionSort);

terminal에 출력된 결과를 보면 동그란 값이 박스 안의 영역 내의 적절한 위치에 삽입이 됨을 볼 수 있다. 이렇게 삽입이 되므로 삽입 정렬이란 이름이 붙었나 싶다.

reverse 테스트

...//
InsertionSort(arr, (reverse = true));
...//

reverse 또한 잘 동작함을 확인할 수 있다. 그런데 여기서 위에서 본 초록색 박스 영역 즉, 점진적으로 앞의 영역은 정렬이 진행된다. 이 말을 바꾸어 말하면 정렬된 영역의 마지막 요소 < 빨간색 값(비교할 값)이라면 삽입하는 동작을 하지 않아도 된다. 따라서 이는 최적의 조건인 배열이 어느정도 정렬이 되어 있을 때 시나리오로 O(N)의 시간 복잡도를 얻을 수 있다.

🛠️ 최적화

삽입 정렬에서의 최적화는 어렵지 않다. 그저 위에서 말한 정렬된 영역의 마지막 요소 < 빨간색 값(비교할 값)이라면 삽입을 위한 동작을 멈추면 된다. 이를 위해 코드를 조금 아래와 같이 수정하자.

// 변경 전
...//
while (j >= 0) {
  if (getCondition(sortedArr[j], sortedArr[j + 1], reverse))
    swap(sortedArr, j, j + 1);
  j -= 1;
}
...//

// 변경 후
...//
while (j >= 0 && getCondition(sortedArr[j], sortedArr[j + 1], reverse)){
  swap(sortedArr, j, j + 1);
  j -= 1;
}
...//

이렇게 getCondition 조건 자체를 루프의 조건으로 넘겨 이미 정렬이 되어 있다면 멈출 수 있다. 따라서, 만약에 모든 요소들이 정렬이 되어있다라고 가정하면 시간 복잡도는 O(N)이 된다.

삽입 정렬에 대해서 정리하자면 아래와 같다.

• 시간 복잡도
  - 정렬이 안 되어있을 때(최악) ⇒ O(N^2)
  - 정렬이 되어있을 때(최선) ⇒ O(N)
• 배열의 앞에서부터 점진적으로 정렬이 진행됨
• 퍼포먼스는 버블 정렬, 선택 정렬보다 좋지만 여전히 낮다.
• 교환 횟수가 적다.

🔥 마치며

삽입 정렬까지 공부하면서 느낀 것은 버블, 선택, 삽입 정렬 중에서 우위를 가리기 힘들다고 생각한다. 삽입 정렬이 버블과 선택 정렬보다 좀 더 우세하다고 하지만 이는 상황에 따라 바뀔 수 있는 미미한 차이라고 생각되기 때문이다. 그래도 삽입 정렬이 정렬되어 있는 경우에도 교환횟수가 버블정렬보다 적으며, 선택 정렬보다 교환횟수가 조금 더 많이 발생하긴 하지만, 이 3개 중 한 개를 택해서 정렬을 진행하라면 삽입 정렬을 택할 것 같다. 그리고 하나 느낀 것이 있는데 삽입 정렬은 이미 정렬된 데이터에 추가 데이터를 넣을 때 효과가 좋을 것 같다.