이렇게.. 머리쓰는 글은 아니다
오늘 문제 중에 소수를 찾는 문제가 있었는데, 이 문제에서 Math.sqrt()가
어디에 어떻게 사용되는지 좀 더 공부해 보기로 하자.
√ Square Root?
우선 무작정 검색해 보았다. Why do we use … sqrt() to check if prime … 뭐 이런 식으로. 다행히 sqrt()로 어떻게 소수를 찾는지 묻는 사람들이 많았는데,
결론적으로 sqrt()로 소수를 찾는 것이 아니라,
소수를 찾을 때 반복을 줄여 리소스를 줄일 수 있는 있어보이는 방법이었다.
isPrimeNum (without sqrt())
의사코드 작성
1이상의 number가 소수인지 확인하는 함수를 가정한다.
function isPrimeNum(number) {
// 매개변수는 number는 1보다 큰 정수를 입력받는다.
// number가 소수인지 아닌지 확인하여 string형태의 문자열로 반환한다.
// 소수는 1과 자기 자신만을 약수로 가지는 수.
// isPrime 변수에 true를 기본값으로 넣어,
// 소수가 아닌 경우를 제외해 본다.
// 1은 소수가 아니다.
// 2의 배수는 소수가 아니다. (단 2를 제외하고)
// 그 외 자기 자신을 제외한 수 중 나누어 떨어지는 수가 있으면
// number는 소수가 아니다.
// (3부터 2씩 증가하여 홀수만 체크)
// isPrime에 따라 문자열을 return한다.
// number은(는) "소수입니다." or "아닙니다."
}코드 작성
function isPrimeNum(number) {
// 매개변수는 number는 1보다 큰 정수를 입력받는다.
// number가 소수인지 아닌지 확인하여 string형태의 문자열로 반환한다.
// 소수는 1과 자기 자신만을 약수로 가지는 수.
// isPrime 변수에 true를 기본값으로 넣어,
// 소수가 아닌 경우를 제외해 본다.
let isPrime = true;
// 1은 소수가 아니다.
if (number === 1) {
isPrime = false;
}
// 2의 배수는 소수가 아니다. (단 2를 제외하고)
if (number % 2 === 0 && number !== 2) {
isPrime = false;
}
// 그 외 자기 자신을 제외한 수 중 나누어 떨어지는 수가 있으면
// number는 소수가 아니다. (3부터 number까지 반복문 필요)
// (3부터 2씩 증가하여 홀수만 체크하면 된다.)
for (let n = 3; n < number; n += 2) {
if (number % n === 0) {
isPrime = false;
}
}
// isPrime에 따라 문자열을 return한다.
if (isPrime) {
return `${number}은(는) 소수입니다.`;
} else {
return `${number}은(는) 소수가 아닙니다.`;
}
}
let result = isPrimeNum(17);
console.log(result);
// 기댓값은 17은(는) 소수입니다.
하지만 값이 커지면?
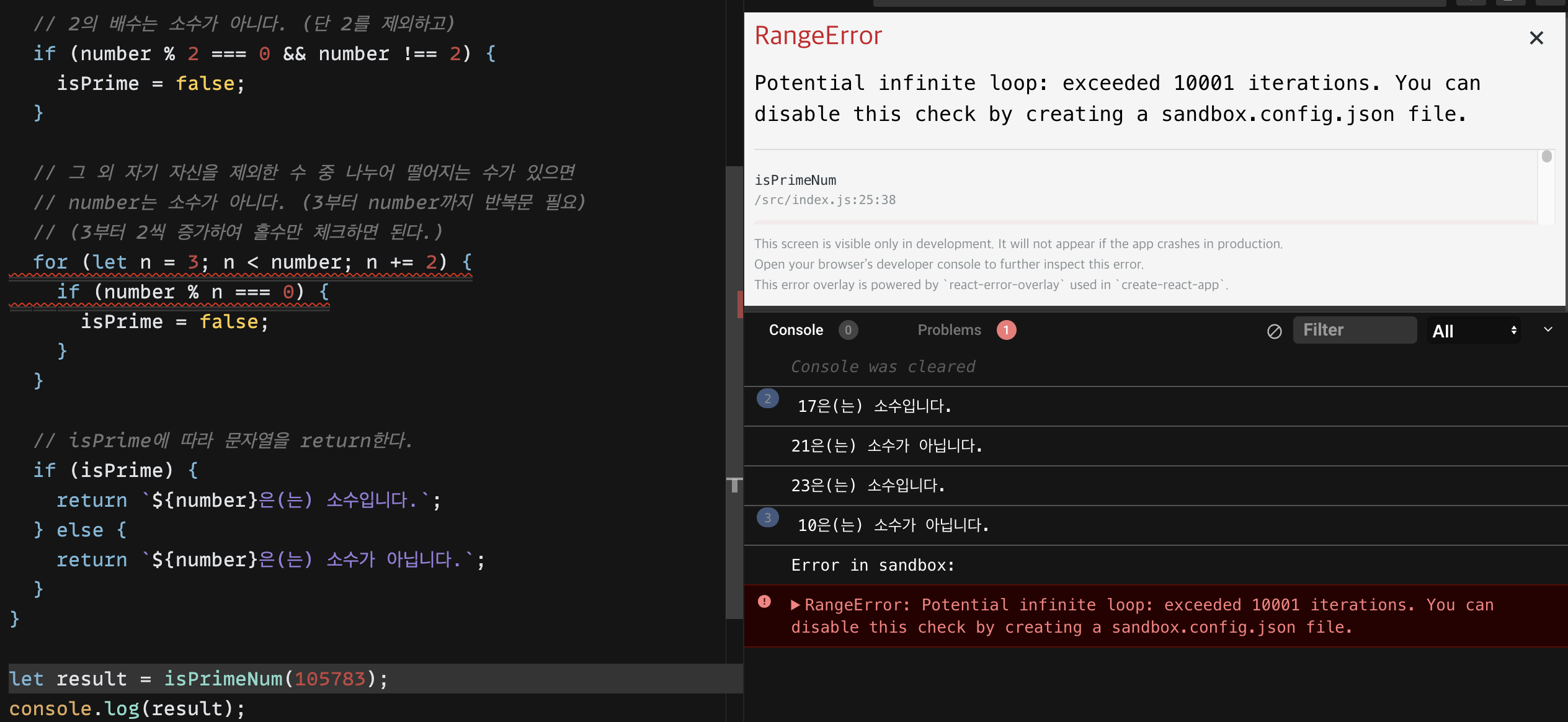
 코드샌드박스에서는 RangeError가 발생한다.
코드샌드박스에서는 RangeError가 발생한다.
대충 10001초과하는 반복이 일어나서 무한 루프라는 경고가 등장한다.
제곱근으로 loop 범위를 줄일 수 있다.
// 모든 범위가 아닌 number의 제곱근까지만
// 나누어보아도 범위를 커버할 수 있다.
// 제곱근까지 포함해야 하기 때문에 =를 추가한다.
let sqrt = Math.floor(Math.sqrt(number))
for (let n = 3; n <= sqrt; n += 2) {
if (number % n === 0) {
isPrime = false;
}
}3부터 number - 1까지 반복하는 것이 아니라, number의 제곱근까지만 체크한다.

당연하다. 전부 실제로 for문 안에 count를 넣어 루프 횟수를 체크해보면 161회만에 105783가 소수인지 아닌지 알 수 있다는 것! 유레카
어떻게 제곱근까지가 모든 범위를 커버할 수 있는 것일까?
너무 깊이 들어가면 이해하기 어려워서 SO에서 찾은 답변 중 가장 잘 이해가 되었던 답변 하나를 가지고 와보았다!!
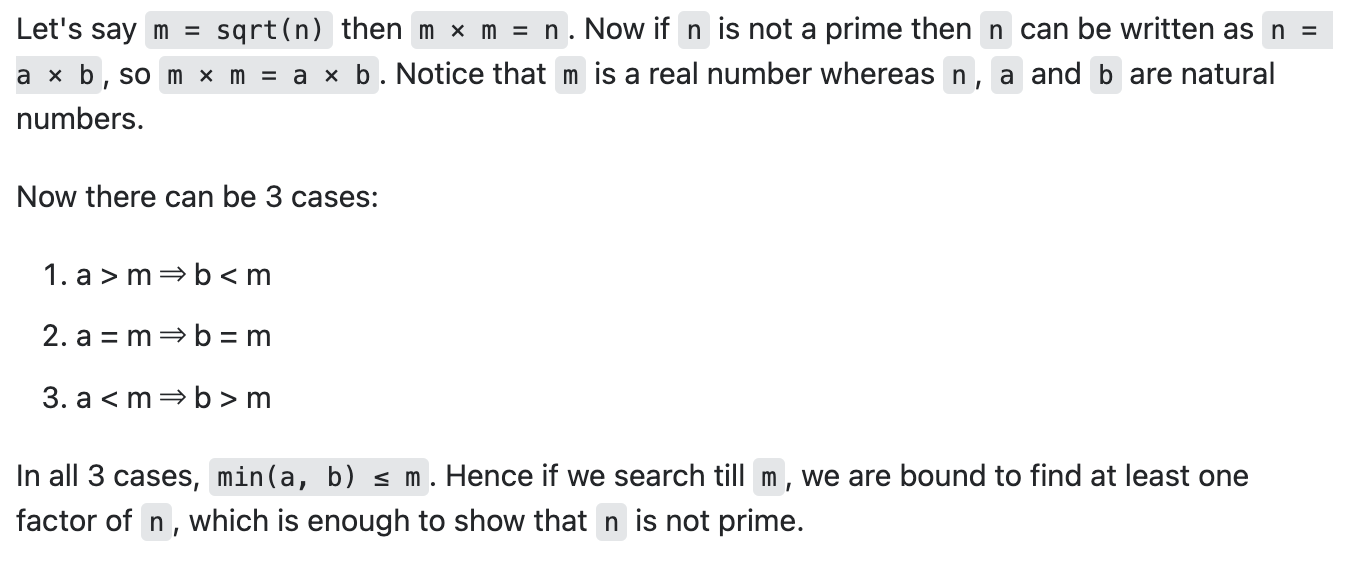 출처 : why-do-we-check-up-to-the-square-root-of-a-number-to-determine-if-the-number-is
출처 : why-do-we-check-up-to-the-square-root-of-a-number-to-determine-if-the-number-is
바쁘다 바빠 현대사회에서
해석해 보면, n이 소수가 아니라고 가정했을 때,
n은 1과 n외의 페어를 이루는 수가 있다.
n을 6이라고 가정하면 1*6=6 외에도 2*3=6이 있다는 당연한 얘기.
2와 3을 a, b라고 해보자.
그리고 정수 외에 6의 제곱근, 실수도 역시 존재한다.
그걸 m이라고 해보자.
그럼 위 이미지와 같이 세가지 경우가 나온다.
a가m보다 크면,b는m보다 작다.a가m과 같으면,b는m과 같다.a가m보다 작으면,b는m보다 크다.
세가지 경우 모두, a, b 중에 작은 것은 m보다 같거나 작다라는 공식이 성립된다.
우리가 n이 소수인지 알아보기 위해서 m까지만 나누어 보아도 하나의 약수는 찾을 수 있기 때문에 소수가 아니라는 사실을 충분히 알 수 있다는 것이다.
원리를 이해하면서 무릎을 탁치며 유레카를 외쳤는데, 막상 정리하다보니 너무 당연한 이야기들을 장황하게 서술한 것 같다. 그런데 원리를 알고나니 절대 잊지 않을 것 같다. 찾는 과정이 매우 보람되고 재미있었다.
같은 의문을 품었던 분들에게 도움이 되면 좋겠다!
끗




잘 보고 갑니다~!