
서론 - Index에 대한 이해
Index라는 단어를 보면 뭐가 제일 먼저 떠오를까?
나의 경우에는 DateBase가 바로 떠오른다.
그럼 인덱스가 무엇인가?
"빠른 검색을 위한 효율적인 데이터 관리 구조"라고 할 수 있을까?
왜? 그 구조는 어떻게 구현되는데??
이러한 생각을 정리하기 위해서 이번 포스트에서는 인덱스에 대한 개념과 구조에 대해 다룰 것이다.
Index ( 인덱스 )
인덱스는 "데이터베이스 테이블의 검색 속도를 높이기 위해 사용하는 구조" 라고 할 수 있다.
DB에서 데이터를 조회해야 하는 작업을 진행한다고 가정해보자.
1부터 100까지의 숫자데이터가 DB에 저장되어 있는 상태에서, 나는 60이라는 데이터를 찾아야한다. ( 가정 )
만약 DB에 데이터를 저장할때에, 순서를 뒤죽박죽으로 넣었다면 나는 60이라는 데이터를 찾기 위해서 테이블 레코드들을 첫번째부터 모두 찾아야 할 것이다. ( DB에서는 이를 Full-Scan 이라고 한다)
이러한 방법은 내가 원하는 특정 데이터를 찾기 위한 방법으로는 비효율적인 방법일 수 있다. 원하는 데이터가 나오기전까지 순차적으로 찾아야 하니까!!
그럼 이런 생각이 들 것이다.
" 애초에 데이터를 삽입할 때에 내가 원하는 기준으로 정렬을 해두면 되지 않나? 그럼 내가 원하는 데이터가 어디쯤에 있는지는 알 수 있잖아!!! "
인덱스는 이러한 관점에서부터 출발하게 된다.
인덱스의 자료구조
그러나 이러한 정렬에서도 정렬한 데이터들을 어떤 자료구조를 이용해 저장할 것인가에 따라 효율이 크게 달라진다.
단순하게만 생각하면 위 예시를 기준으로 60이라는 데이터를 찾기 위해서 정 가운데를 찾고, 값이 50이라면 60은 그보다 크므로 50보다 작은 절반 데이터를 탐색할 필요가 없으므로 절반씩 줄여나가는 이분탐색 구조가 잘 어울릴 것 같지 않은가??
그럼 실제로 인덱스는 이분탐색 Linked-List를 사용할까? ( 배열은 크기가 고정이므로 배제하자 )
결론은 NO!!! 아니다!
링크드 리스트도 충분히 고려할 수 있지만, 인덱스를 사용하는 DB특성상 대용량 데이터를 처리해야할 상황이 많을 것이다.
이 때, 선형구조인 링크드 리스트를 사용할 경우에 데이터를 반씩 잘라 접근한다 하더라도 링크드 리스트의 특성인 순차적 접근은 시간이 오래 걸릴수 있어 비효율적이다.
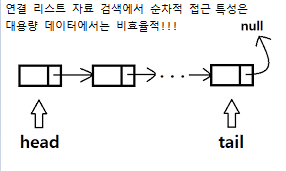
그렇기에 인덱스에서는 트리 구조를 사용한다.
자세히 말하자면 해시 트리 구조인데, 이는 밑에서 B-tree, B+tree에 대해 얘기하며 설명하겠다.
트리 구조가 유용한 이유는?
트리 구조가 유용한 이유는 "순차적 접근이 아니기 때문"이다.
트리 자료구조를 생각해보자
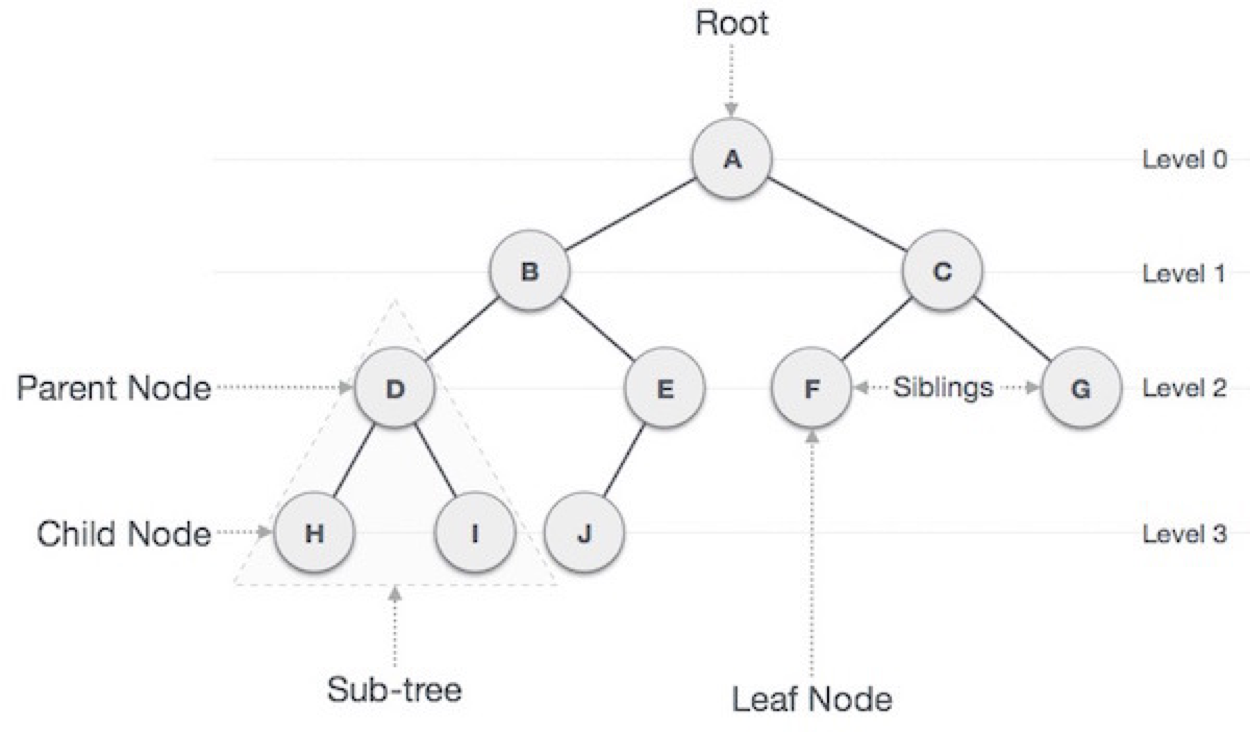
위 사진과 같이 트리 구조에서 이분탐색과 같은 방법을 적용할 때를 생각해보자.
내가 봐야 하는 절반 데이터 서브트리의 루트 노드에 접근하기 위해서 단순히 현재 노드와 연결되어 있는 링크를 따라가면 된다.
Linked-List에서는 절반을 무시한다 하더라도
ex :
1~100까지의 데이터에서 60이라는 데이터를 찾기 위해서 처음 50을 찾고
60은 50보다 크므로 51~100 까지만을 남길때
다음 50개의 데이터의 중앙값인 75에 접근하기 위해서 순차적으로 넘어가야 한다.
내가 다음 찾을 기준점 값은 75이지만 현재 50에서 75까지 가기 위해서 51,52,53,54.... 75로 차례대로 가야한다.
그러나 Tree구조에서는 이러한 순차적 접근이 아닌 현재 노드와 연결된 노드로 넘어가면 되므로 굉장히 효율적이라고 할 수 있겠다!!!
50노드와 연결되어 있는 다음 노드는
1. 50보다 작은 데이터의 절반인 25데이터를 가지는 노드가 left-child로 연결.
2. 50보다 큰 데이터의 절반값인 75데이터를 가지는 노드가 right-child로 연결.
- 50에서 바로 25, 75로 갈 수 있음!!
Binary Search Tree로는 충분한가?
그럼 Binary Search Tree구조를 인덱스에 적용할까??
Linked-List보다는 좋은 선택이지만 "대용량 데이터 탐색 및 관리"의 측면에서 더 좋은 구조로 인덱스 자료구조를 만들 수 있지 않을까??
위에서 계속 들었던 예시처럼 숫자를 예로 들어보자.
기존 이진 트리의 경우에는 내가 6이라는 데이터를 찾기 위해서 현재 노드의 값이 4인데 ( 4라고 가정했다 ) 6은 4보다 크므로 right-child-node로 이동하면 된다.
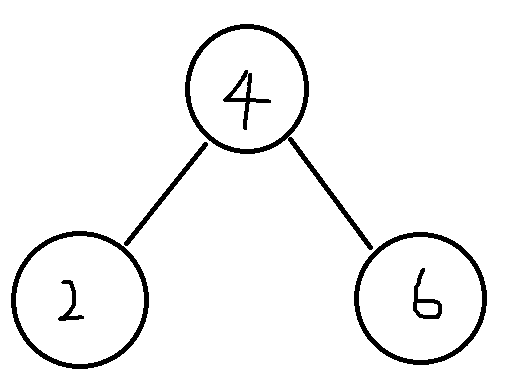
그런데 이러한 구조로 인덱스를 만들게 되면, 데이터가 많아질수록 트리의 깊이가 커지지 않을까??
맞다!
트리의 깊이가 커지면 트리의 불균형을 초래할 수 있거나, 탐색에서 타고 들어가야 하는 노드의 수가 늘어나기 때문에 좋은 방법이 아니다.
ex ) 500이 루트노드의 값이고 500보다 작은 값들이 큰 값들보다 훨씬 많다면, 루트 노드 기준 왼쪽만 너무 무거워지게 된다.
이러한 단점을 개선하기 위해서 B-tree, B+tree가 나오게되었다.
B-tree
B-tree의 경우에는 하나의 노드가 여러개의 키, 데이터 값을 가질 수 있다.
이 구조는 이진 트리가 아닌데, 이 구조의 장점은 기존 Binary-Search-Tree보다도 작은 사이즈를 가지는 트리로 인덱스를 저장할 수 있다는 것이다.
이러한 장점은 데이터 검색 속도에서도 효과를 드러내는데, 트리의 높이가 작아지는 만큼 데이터를 찾기 위한 탐색의 깊이가 줄어드므로 성능을 향상시킬 수 있다.
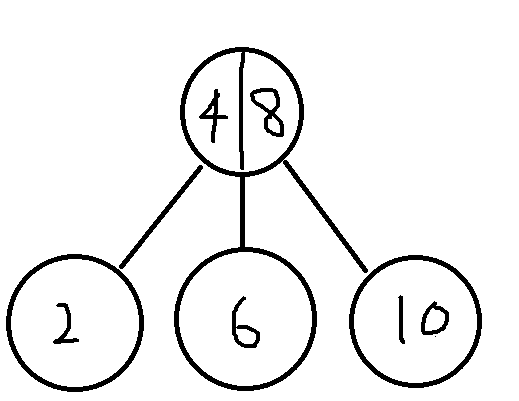
B+tree
근데 만약 단일 데이터 검색이 아닌, 특정 범위 데이터 검색을 해야하는 일이 생기면 어떻게 될까??
위 B-tree구조에서는 조금 비효율적이라고 생각되지 않은가? 자식노드를 갔다가, 다시 부모노드, 그리고 또 다른 자식노드....
굉장히 비효율적이다.
이를 개선하기 위해서 B+tree가 고안되었다.
B+tree 구조에서는 각 노드가 키값만을 가진다.
데이터는 어디로 갔지?? 라고 생각할 수 있는데, 데이터는 최하단의 리프노드에 저장이 된다. ( Cluster Index 기준으로 얘기하겠다 )
아니 이게 효율적이야? 라고 또 물어볼 수 있는데, 효율적이다.
각 리프노드끼리는 서로 Linked-List처럼 연결되어 있기에 특정 데이터 범위를 검색하기 위해서 범위 내에 해당하는 데이터를 하나만 찾게 되면 연결되어 있는 다른 리프노드를 타고들어가면 된다!!
굉장히 효율적이지 않은가!!?!
마무리
오늘은 이렇게 인덱스의 구조가 어떻게 이루어지는지 찾아보았다.
다음 포스트에서는 이러한 인덱스 구조를 적용한 Cluster Index, Secondary Index ( Non-cluster Index ) 에 대해서 알아보겠다.
MySQL의 InnoDB, MyIsam이 이와 관련되어 있으므로 궁금하면 다음 포스트를 확인하자!
