[이진탐색] Leet code 240. Search a 2D Matrix II

리트코드 240번
왼쪽에서 오른쪽 위에서 아래로 오름차순 정렬된 행렬에서 target값 찾기

시도1

class Solution:
    def searchMatrix(self, matrix, target: int) -> bool:
        m, n = len(matrix), len(matrix[0])

        first_m, first_n = 0, 0
        last_m, last_n = m - 1, n - 1

        while first_m <= last_m and first_n <= last_n:
            mid_m, mid_n = first_m + (last_m - first_m) // 2, first_n + (last_n - first_n) // 2

            if matrix[mid_m][mid_n] == target:
                return True

            elif matrix[mid_m][mid_n] > target:
                if mid_m - 1 < 0 :
                    last_m, last_n = mid_m, mid_n - 1
                elif mid_n -1 < 0 :
                    last_m, last_n = mid_m - 1, mid_n
                elif matrix[mid_m - 1][mid_n] > matrix[mid_m][mid_n - 1]:
                    last_m, last_n = mid_m - 1, mid_n
                else:
                    last_m, last_n = mid_m, mid_n - 1

            else:
                if mid_m + 1 > last_m:
                    first_m, first_n = mid_m, mid_n + 1
                elif mid_n + 1 > last_n:
                    first_m, first_n = mid_m + 1, mid_n
                elif matrix[mid_m + 1][mid_n] < matrix[mid_m][mid_n + 1]:
                    first_m, first_n = mid_m + 1, mid_n
                else:
                    first_m, first_n = mid_m, mid_n + 1

        return False

• 이진탐색을 2차원으로 진행하면되겠다고 생각
• matrix[m][n]이라고 한다면 first_m, first_n, last_m, last_n으로 확장하고 각각 mid를 계산 -> mid_m, mid_n
• 만약 target이 5라면 먼저 중간값인 9와 비교해서 더 작기 때문에 9보다 더 작은 위쪽과 왼쪽 중에 더 큰쪽으로 last를 옮겨서 계속 진행합니다

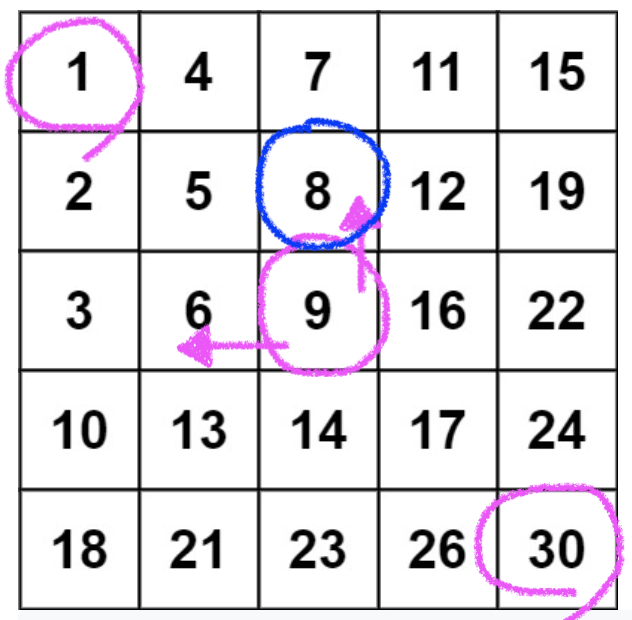
• 이진탐색과 같은 원리라고 생각해서 처음에 이렇게 확신하고 풀었지만.... 예외들이 나왔고 왜그런지 가만 생각해보니 물론 9보다 왼쪽 그리고 위쪽이 더 작은 것들은 확실하지만 노란색 부분들에도 더 작은 숫자가 있을 수 있으니 모두 탐색했다고 볼수가 없기 때문에 안되는것... 하ㅠㅠㅠ 이런거 잘 체크해야겠다..

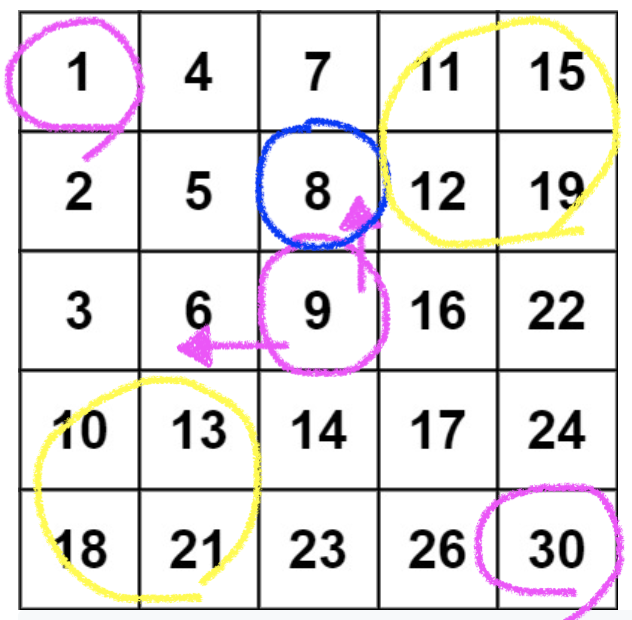
풀이1

제대로된 풀이 중 하나는 오른쪽위나 왼쪽 아래에서부터 시작해서 작거나 크면 col , row값을 조정하면서 내려가는 것입니다.

여기서는 오른쪽 위에서 시작하도록 하겠습니다

class Solution:
    def searchMatrix(self, matrix, target: int) -> bool:
        row, col = 0, len(matrix[0]) - 1

        while row < len(matrix) and col > -1:
            if matrix[row][col] == target :
                return True
            elif matrix[row][col] > target:
                col = col - 1
            else:
                row = row + 1

        return False

• 그림처럼 15에서 출발해서 target보다 작으면 아래로 target보다 크면 왼쪽으로 이동하면서 구하고 만약 범위를 벗어나면 False을 반환하는 방식입니다

• 이게 위와 다르게 되는 이유는 target이 20이라면 15보다 크기때문에 밑으로 내려갈때 15로부터 왼쪽은 모두 제외되고 따라서 이런식으로 하다보면 왼쪽과 아래쪽만 고려해주면되고 오른쪽과 위쪽은 지나온 곳이기 때문에 이미 따져졌다고 볼 수 있기 때문입니다

• 결국 이문제는 기준을 어디로 잡느냐가 중요한문제...

• 이진탐색을 쓴건 아니므로 복잡도는 O(m+n)이 나오게 됩니다

  
  
  
  

  풀이2

  이번에는 그냥 각 행마다 이진탐색 적용을 해서 찾는 방법입니다

  class Solution:
    def searchMatrix(self, matrix, target: int) -> bool:
        rows = len(matrix)
  
        for row in range(rows):
            first, last = 0, len(matrix[0])-1
            while first <= last:
                mid = first + (last - first) // 2
  
                if matrix[row][mid] == target:
                    return True
                elif matrix[row][mid] > target:
                    last = mid - 1
                else:
                    first = mid + 1
  
        return False

• 복잡도는 최악일 경우 O(nlogm)이지만 중간에 찾는다면 나쁘지 않은 것 같아 시도해봤고 실제로 위에 코드와 비슷하게 나왔습니다