최단경로
1. 자료구조 알고리즘 5주차 강의
1-1 최단경로
1-1-1 개념, 구현
1. 그래프로 표현. 각 지점은 노드, 도로는 간선.
2. 다익스트라, 플로이드-워셜1-2 다엑스트라 알고리즘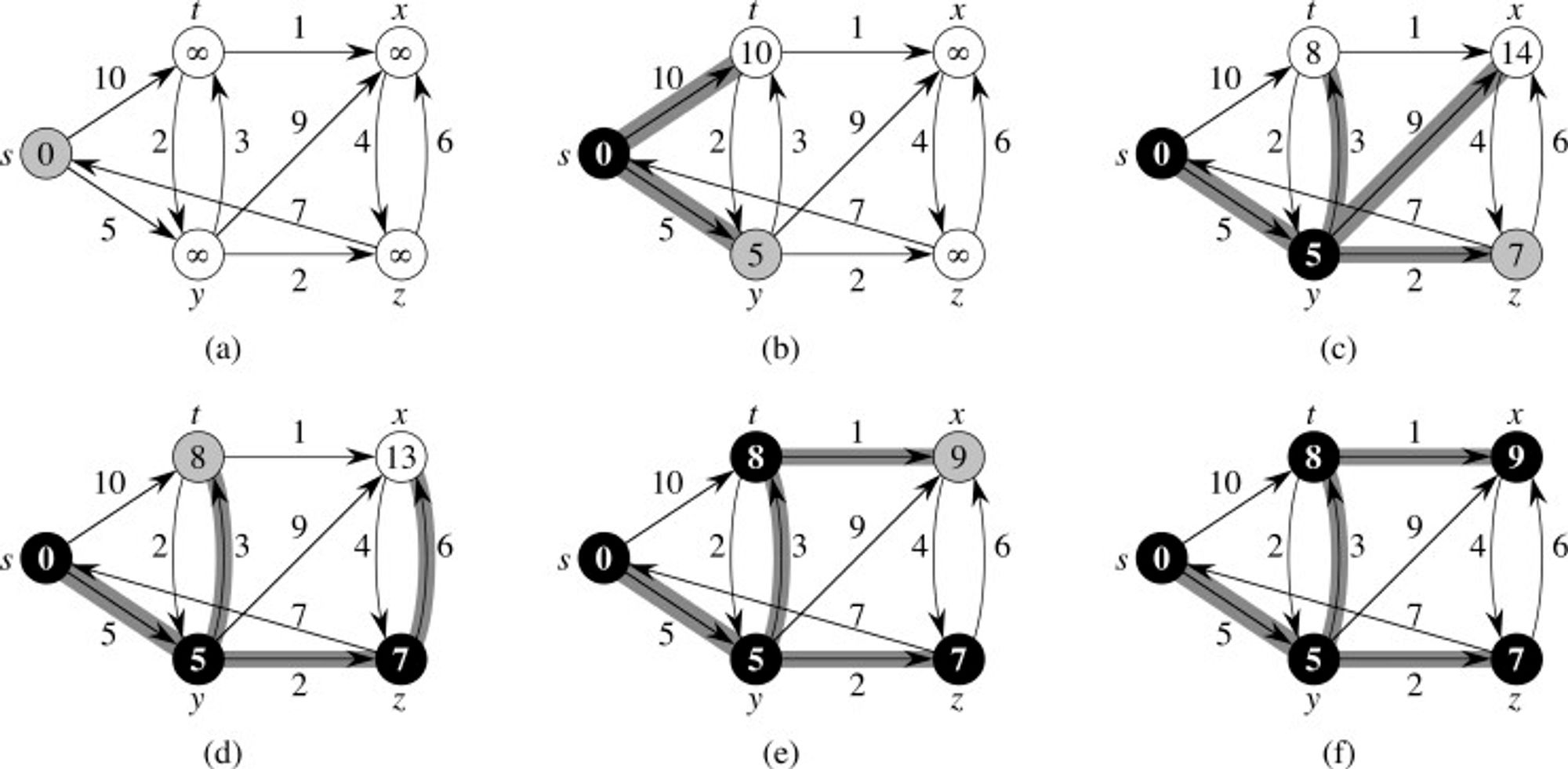
1. 출발지 = s
(s, t, x, y, z 순)
거리 = [0, inf, inf, inf, inf]
방문 = [True, False, False, False, False]
2. 갈 수 있는 노드들의 최소거리를 측정
s->t: 10
s->y: 5
(s, t, x, y, z 순)
거리 = [0, 10, inf, 5, inf]
방문 = [True, False, False, False, False]
3. 방문 안한 녀석들 중 가장 가까운 녀석인 y를 방문하고, 최소거리를 측정
y->t: 3
y->x: 9
y->z: 2
(s, t, x, y, z 순)
거리 = [0, 8, 14, 5, 7]
방문 = [True, False, False, True, False]
4. 방문 안한 녀석들 중 가장 가까운 녀석인 z를 방문하고, 최소거리를 측정
z->x: 6
(s, t, x, y, z 순)
거리 = [0, 8, 13, 5, 7]
방문 = [True, False, False, True, True]
5. 방문 안한 녀석들 중 가장 가까운 녀석인 t를 방문하고, 최소거리를 측정
t->x: 1
t->y: 2
(s, t, x, y, z 순)
거리 = [0, 8, 9, 5, 7]
방문 = [True, True, False, True, True]
6. 방문 안한 녀석들 중 가장 가까운 녀석인 x를 방문하고, 최소거리를 측정
x->z: 4
(s, t, x, y, z 순)
거리 = [0, 8, 9, 5, 7]
방문 = [True, True, True, True, True]
7. 방문 안한 노드가 없으므로 끝낸다.
(s, t, x, y, z 순)
거리 = [0, 8, 9, 5, 7]
방문 = [True, True, True, True, True]
문제풀이
2. 문제풀이
2-1 11729. 하노이 탑 이동 순서
2^n-1번의 이동 필요
a, b, c기둥이 있을 때 a=>c로 이동, 원반이 n개가 있을 때:
1. n=1일 때는 옮기고 종료
2. n-1개를 b 기둥에 옮긴다(재귀)
3. 가장 큰 원반을 c 기둥에 옮긴다
4. n-1개를 c 기둥에 옮긴다(재귀)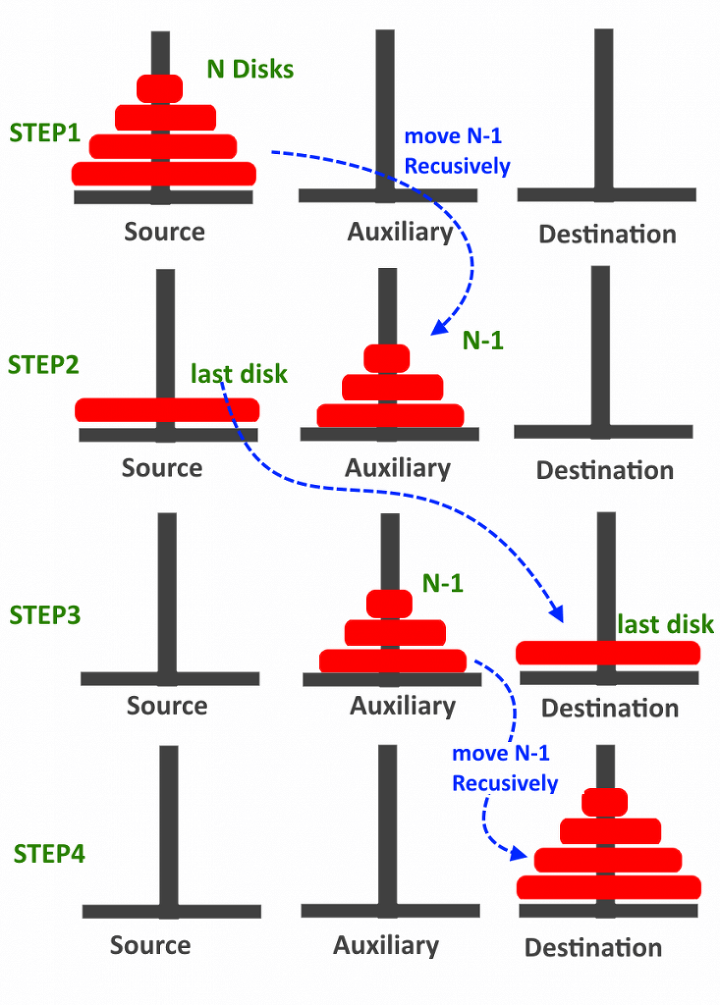
2-2 11651. 좌표 정렬하기 2
아래 형식을 이용하여 풀수 있음 arr.sort(key=lambda x:(x[1],x[0])) arr = [[a,b,c...], [d,e,f...], ..... , [x,y,z...]] 일때
x: x[i] => i번째 원소들끼리 비교
x:(x[i],x[j]) => i번째 원소끼리 비교 후 같다면, j번째 원소를 비교
2-3 2108. 통계학
산술평균 : N개의 수들의 합을 N으로 나눈 값
중앙값 : N개의 수들을 증가하는 순서로 나열했을 경우 그 중앙에 위치하는 값
최빈값 : N개의 수들 중 가장 많이 나타나는 값.
=> 여러 개 있을 때에는 최빈값 중 두 번째로 작은 값을 출력한다.
범위 : N개의 수들 중 최댓값과 최솟값의 차이
정렬 후 풀면 최빈값 말고는 다 풀수가 있다.
1. n만큼 돌면서 하는 방법value = [arr[0]]
count = [1]
for i in range(1,n):
if value[-1] == arr[i]:
count[-1] += 1
else:
value.append(arr[i])
count.append(1)
max_count = max(count)
c = 0
v = 0
for i in range(len(count)):
if count[i] == max_count:
v = value[i]
c += 1
if c == 2:
break
print(v) 2. collections를 쓰는 방법from collections import Counter
min = Counter(arr).most_common(2)
if len(min) > 1:
if min[0][1] == min[1][1]:
print(min[1][0])
else:
print(min[0][0])
else:
print(min[0][0])