정렬
1. 자료구조 알고리즘 4주차 강의
1-5 Quicksort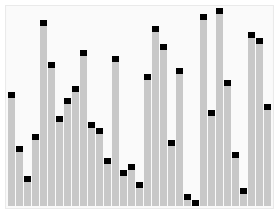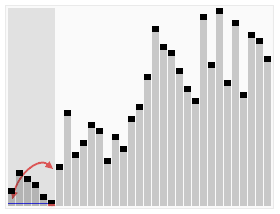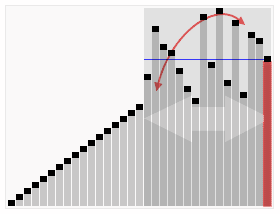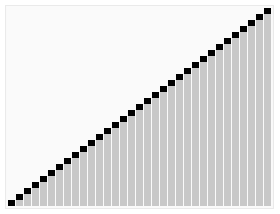
1-5-1 개념, 구현
1. 배열에서 마지막 원소를 기준(pivot)을 잡는다
2. 기준보다 값이 작은 집합과 큰 집합으로 나눈다(Divide).
==> 과정: 기준보다 큰값을 바로 전에 나온 작은값과 위치를 바꾼다
==> 마지막에 기준값을 사이에 넣는다
3. 나눈 두 집합에 대해 1,2를 반복(재귀 호출)
1-5-2 시간 복잡도
O(N*log(N)) <= Quicksort <= O(N²)1-7 병합 정렬
:각각 나누었다가 합치면서 대소비교를 한다 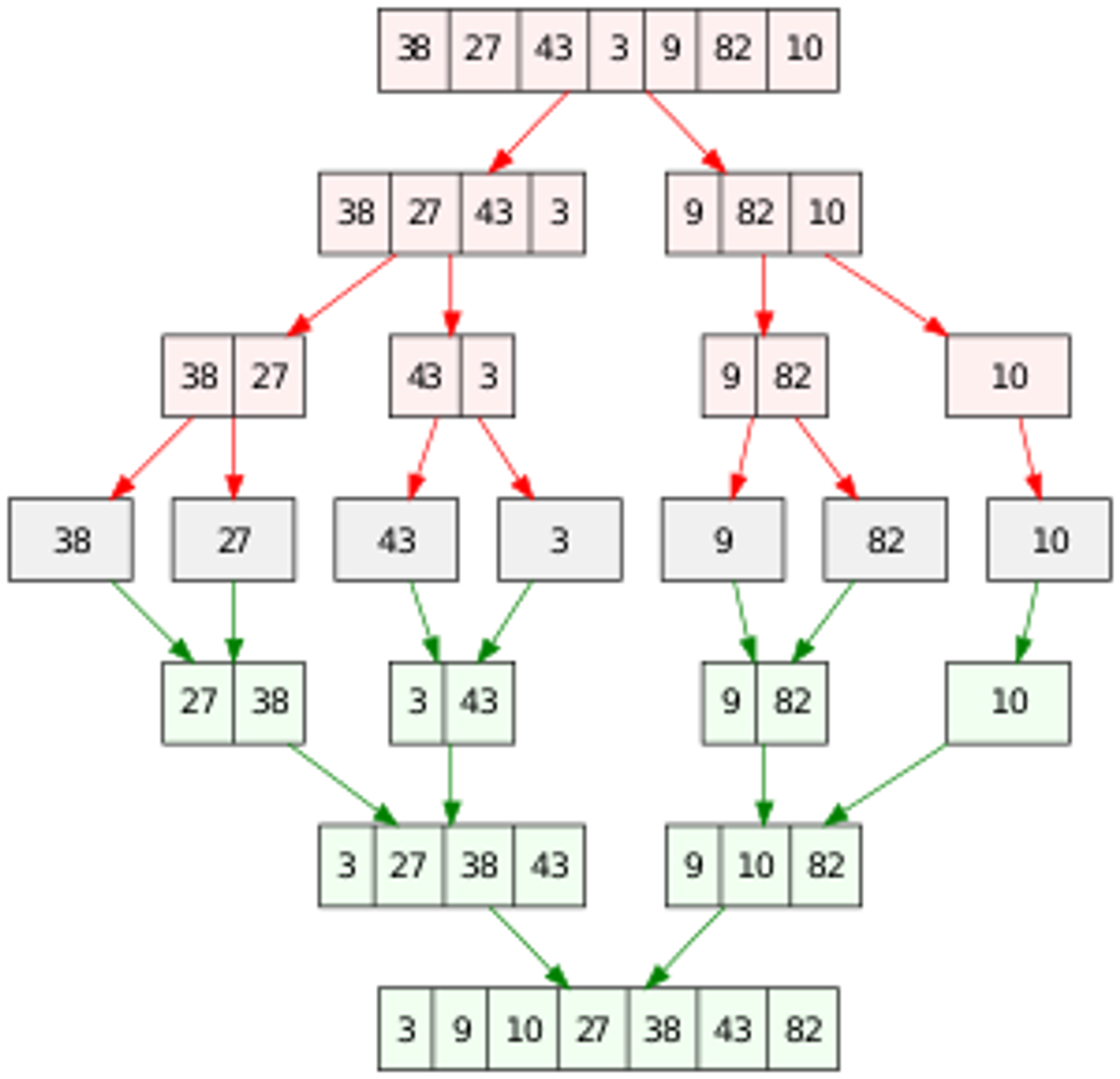
1-7-1 개념, 구현
1. 배열의 원소가 1개일때까지 나눈다.
2. 나눈 배열들을 가지고 아래 3,4을 반복하여 병합한다
3. 정렬된 두 배열 A, B, 빈 배열 C
4. A[i], B[j]의 첫번째 값 비교(i,j = 0)
==> 작은 값을 C에 넣고 작은 값이 있던 배열의 인덱스 증가
==> A,B의 모든 값을 비교 할 때까지 2 반복
5. C = 정렬된 배열
1-7-2 시간 복잡도
무조건 평균 O(N*log(N))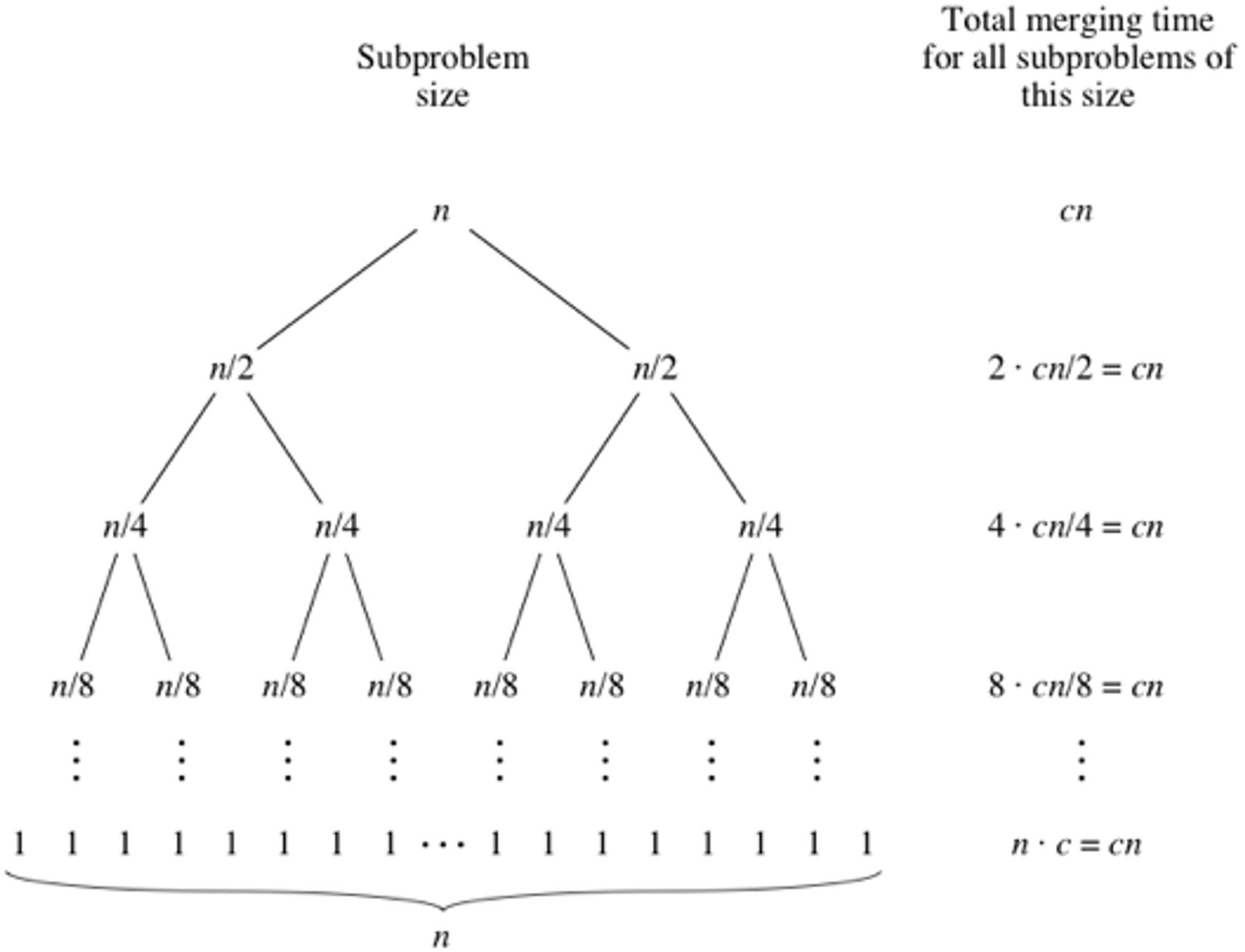
1-8 힙 정렬
:힙? = 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리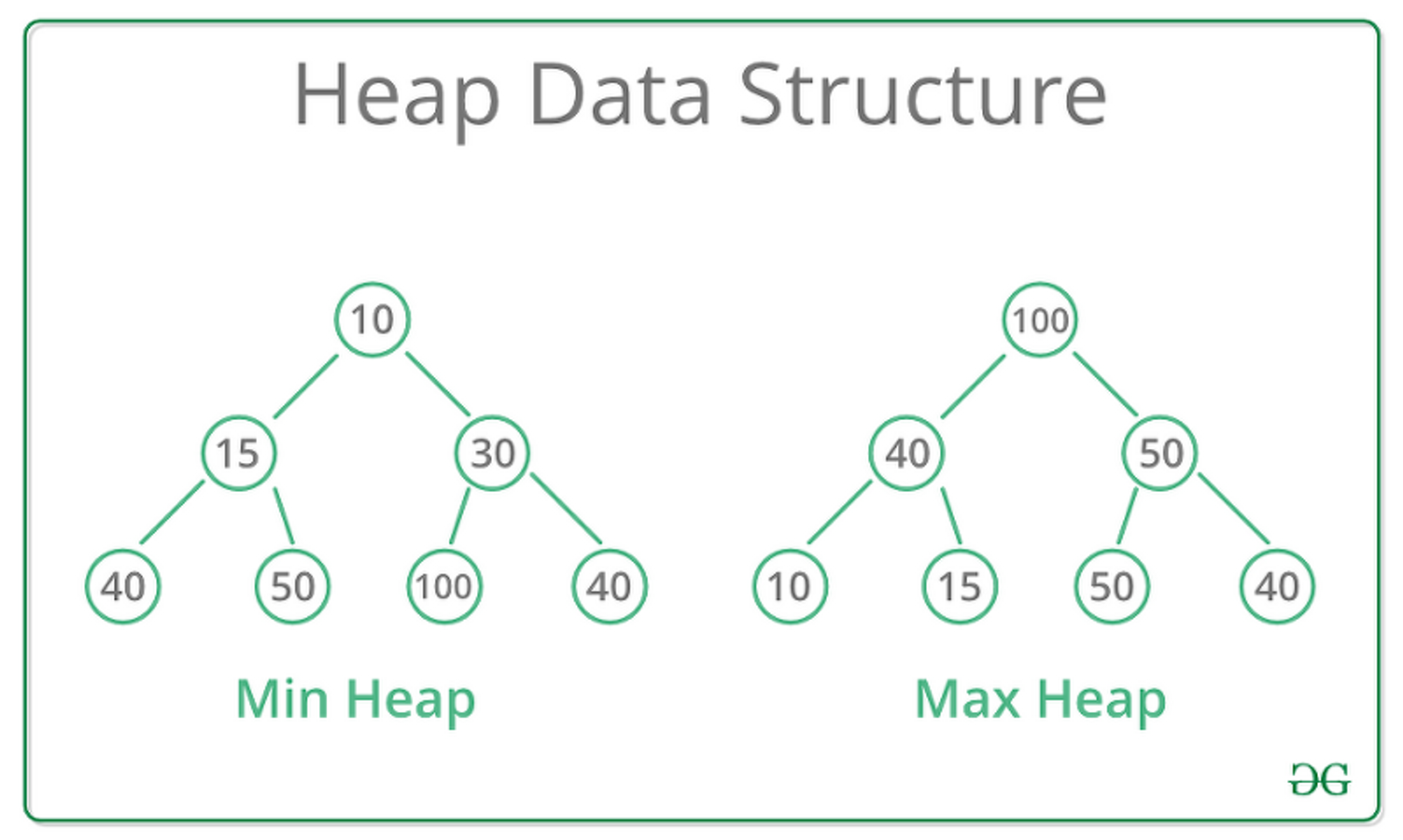
1-8-1 개념, 구현 (힙은 기본이 최소)
1. 최소 힙 만들기
2. 최소값을 하나씩 빼서 배열에 넣는다
(최대 힙이라면 배열을 뒤집으면 됨)
1-8-2 시간 복잡도 = 이진트리의 높이
완전 이진트리의 최대 높이 = O(log(N))
따라서 시간복잡도 = O(log(N))
문제풀이
2. 문제풀이
2-1 9184. 신나는 함수 실행
1. 3차원 배열을 만드는 것이 핵심
2. 그 배열의 값들을 모두 저장 (a,b,c <=20)
3. 배열[a][b][c] => 정답2-2 2579. 계단 오르기
max값을 배열에 저장
i = 현재 계단
M[i] = 계단이 i까지 있을 때 가장 큰값
V[i] = 현재 계단의 값
1. 바로 전 계단에서 옴 : M[i-3] + V[i-1] + V[i]
2. 한칸 띄어 옴 : M[i-2] + V[i]
3. 1,2를 비교하면 M[i]의 쵀댓값을 구할 수 있다
4. M[0],M[1],M[2] 값을 구하면 M[3]부터는 자동으로 구하기 가능!
5. M[0] = V[0]
6. M[1] = V[0]+V[1]
7. M[2] = max( V[0]+V[2], V[1]+V[2])
2-3 11053. 가장 긴 증가하는 부분 수열
1. 가장 큰 부분 수열의 '길이'만 알면 된다
2. 부분수열을 만드는 도중에 필요한 것:
1) 부분 수열의 마지막 값 (대소비교)
2) 수열의 길이
1. A[i] 수열의 값이 들어있는 리스트
2. B[i] [0]부터 시작하는 빈 리스트
3. A[i] > B[-1] ==> B에 A[i]를 삽입
4. A[i] <= B[-1] ==> 새로운 부분 배열의 시작임
B안의 값들과 비교를 해나감
if B[j] >= A[i]: B값이 크거나 같은 값이 나오면
B[j] = A[i] 그 값을 A[i와 교체]
5. 3,4 반복