뜨리를 알아보자.
트리는 당신이 생각하는 크리스마스 트리가 맞다.
곧 크리스마스가 다가오는데 오늘은 코딩을 통해 크리스마스 트리를 만들어 보는 것이 어떨까?
코공 : 썸녀야.. 이번 크리스마스에 나랑 같이 집에서 크리스마스 Tree.. 만들지 않을래?
썸녀 : (심쿵) 응응!
크리스마스 늦은 밤..
둘은 함께 binary tree를 만들었고 훗날 코딩테스트에서 멋진 Tree를 구현해 취업에 성공했다고 한다..
코로나인데 나가지 말고 Tree 코드나 구현하자. 이번 크리스마스. 벌써 달달하다.
모든 목차는 부트캠프에서 주는 질문을 기반으로 만들었습니다.
Tree
트리도 자료 구조의 한 종류이다. 먼저 최상위 노드(root)가 있고, 루트를 중심으로 밑에 child를 추가하며 층을 쌓으며 나아가는 구조이다.
그림을 보면 바로 알 수 있다.
내가 그린 Tree 그림이다.
Tree 용어
그림을 같이 보자
- Node : 각 데이터 들을 Node라고 한다. 그림에서는 A~I가 모두 Node이다.
- Root : 위 그림의 A처럼, 트리 구조에서 최상위에 존재하는 노드를 root라고 한다.
- Edge : 노드와 노드를 이어주는 선
- Parent : 트리는 부모와 자식이 존재한다. 각 노드의 윗부분이 부모가 되는 것. C, F의 부모는 B / B와 H의 부모는 A
- Child : 자식. 한 노드를 중심으로 왼쪽, 오른쪽 밑에 있는 애들이다.
위에는 이진 트리라서 자식이 2명이 최대이다. 자식은 2명 이상일 수 있다.
B의 자식은 C,F / C의 자식은 D, E - Leaf : 더 이상 자식이 없는 Node들을 leaf라고 한다.(아마 당신도 leaf가 될 수 있다.ㅠ-ㅠ) 그림에서는 D, E, F, G, I가 되겠지?
- Siblings : 말 그대로 형제. 부모가 같은 노드들을 씨ㅂ링 이라 한다. [C, F], [D, E], [G, I] 요렇게 서로 형제다.
- Path : 출발 노드에서 목적지 노드로 가는 경로에 있는 노드들이다. A에서 I로 가는 경로는 A-H-I
- length : Path의 길이이다. A부터 I까지의 길이는 2.
- Depth : 루트(root)에서 어떤 노드까지의 경로 길이이다. 그림에서 G의 깊이는 2, E의 깊이는 3이다. 오른쪽 세로 선을 살펴보자.
- Height : Tree의 Root에서 가장 밑에 있는 Node까지의 길이이다. 즉 Tree의 전체 길이, Tree의 키라고 생각하면 될 듯. 그림의 Tree의 길이는 4. 오른쪽 세로 선을 살펴보자.
- level : 간단히 말해 레벨은 깊이(Depth)에 1을 더한 값
그 외의 용어들도 있다. level, degree 등.. 더 있지만 일단 기본적인 것들, 내가 아는 것들만 적어 보았다.
혹여나 내가 알고 있는 용어의 개념들이 틀리다면 수정부탁 wind.
Tree와 Graph의 차이점
부트캠프에서 준 질문이다. 부트캠프 질문은 좋은 질문이니까 찾아보자.
Graph
- Edge에 방향을 정할 수 있으며 정점에 달린 Edge가 여려 개 가능. / 무방향, 방향
- self loof, cycle개념이 있다.
- 노드 끼리 부모, 자식, 형제, 루트 개념이 없다.
- 네트워크 모델이다. (네트워크가 궁금하다면 이미지 검색을 하면 알 수 있다.)
- 순환으로 DFS, BFS가 있다.
Tree
- 정점(노드)에 Edge는 반드시 1개.
- loof가 없다.
- 가족같은 Tree 기업
- 계층 모델
- 전위, 중위, 후위 순환이 있다. DFS, BFS에 포함된 것들.
DFS와 BFS 비교
DFS(Depth First Search) : 깊이 우선 탐색
루트 노드(혹은 다른 임의의 노드)에서 시작해서 다른 가지로 넘어가기 전에 해당 가지를 끝까지 탐색하는 방법.
그림을 보고 이해하자.
Node안에 있는 숫자들이 DFS가 Tree를 탐색하는 순서이다.
특징
모든 노드를 방문 하고자 하는 경우에 이 방법을 선택한다.
깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단하다.
단순 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느리다.
전위, 중위, 후위 탐색이 모두 DFS에 속한다.
스택을 사용.
BFS(Breadth First Search) : 넓이 우선 탐색
루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법
그림을 보고 이해하자.
Node안에 있는 숫자들이 BFS가 Tree를 탐색하는 순서이다.
그림처럼, 같은 깊이에 있는 아이들을 먼저 다 탐색하고 다음 깊이로 넘어간다.
특징
두 노드 사이의 최단 경로, 혹은 임의의 경로를 찾고 싶을 때 이 방법을 사용.
깊이 우선 탐색보다 복잡하다.
어떤 노드를 탐색했는지 반드시 검사해야 하고, 검사를 안 하면 무한루프에 빠질 수 있다.
큐를 사용.
모두 코드로 구현까지 하고 싶지만 능력 부족.
이진 트리의 종류 / Binary Tree
Binary Tree
각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료 구조로, 자식 노드를 각각 왼쪽 자식 노드와 오른쪽 자식 노드라고 한다.(위키백과)
또한, 각 노드의 크기는 반드시 왼쪽 < 부모 < 오른쪽 이다.
왼쪽은 부모보다 작고, 오른쪽은 부모보다 크다.
이진트리는 노드가 2개를 초과할 수 없다. 왜냐? 그것이 이진 트리니까.
정 이진 트리
정 이진 트리(full binary tree)는 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리다.
오른쪽은 D의 자식이 1개라서 정 이진 트리가 아니다.
D의 의지를 잘 이어가자.
완전 이진 트리
완전 이진 트리(complete binary tree)에서, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가능한 한 가장 왼쪽에 있다. 마지막 레벨 h 에서 1부터 2h-1 개의 노드를 가질 수 있다.
오른쪽은 완전 이진 트리가 아니다. 왜냐? 마지막 level인 H를 제외하고 H보다 위에 있는 모든 노드들이 2개씩 다 있어야 한다.
즉, H 위로 다 집합해
포화 이진 트리
포화 이진 트리(perfect binary tree)는 모든 내부 노드가 두 개의 자식 노드를 가지며 모든 잎 노드가 동일한 깊이 또는 레벨을 갖는다.
오른쪽은 포화 이진 트리가 아니다. 왜냐? D가 자식이 없다. 꽉꽉 채우라 이말이야.
위에서 말했지D의 의지를 이으라고
전위, 중위, 후위 순회
부모가 어디에 오냐 따라 전, 중, 후로 나뉜다. 부모가 앞이면 전, 가운데면 중, 마지막이면 후.
모두 깊이 우선 탐색의 한 종류라는 것을 기억하자. 그래서 왼쪽을 볼 때 자식이 있으면 깊이 우선이라 자식을 또 탐색한다.
그림을 통해 살펴보자.
전위 순회(Preorder Traversal): 부모 → 좌 → 우
전위 순회 번호! 노드에 있는 번호대로 전위 순회가 탐색을 한다.
부모가 먼저니까 1 -> 좌를 살펴서 2 -> 또 좌가 있어서 3-> 또 좌가 있어서 5 -> 3은 봤으니까 이제 우로 가서 5 -> 3번 가족 다 봤으니 2의 우로 가서 6-> 6이 부모니까 좌인 7 -> 우 8 -> 2번 가족 다 봤으니 1의 우로 가서 9 -> 9의 좌인 10 -> 좌가 있으니까 11 -> 마지막 12
중위 순회(Inorder Traversal): 좌 → 부모 → 우
중위 순회 번호! 노드에 있는 번호대로 전위 순회가 탐색을 한다.
중위 순회는 tree를 크기 순으로 정렬할 때 쓰인다.
가장 간단하게 생각하는 것은, 왼쪽 벽면에서 가까운 노드부터 차례대로.
내가 3의 위치를 잘못 그려서 그런데 2보다 오른쪽에 있어야 한다..
후위 순회(Postorder Traversal): 좌 → 우 → 부모
후위 순회 번호! 노드에 있는 번호대로 전위 순회가 탐색을 한다.
BST 코드 (BinarySearchTreeNode)
1. 기본 뼈대.

부트캠프가 만들어줌. 친절하다 친절해.
기본적으로 부모, 왼쪽, 오른쪽을 만들어 준다.
2. insert
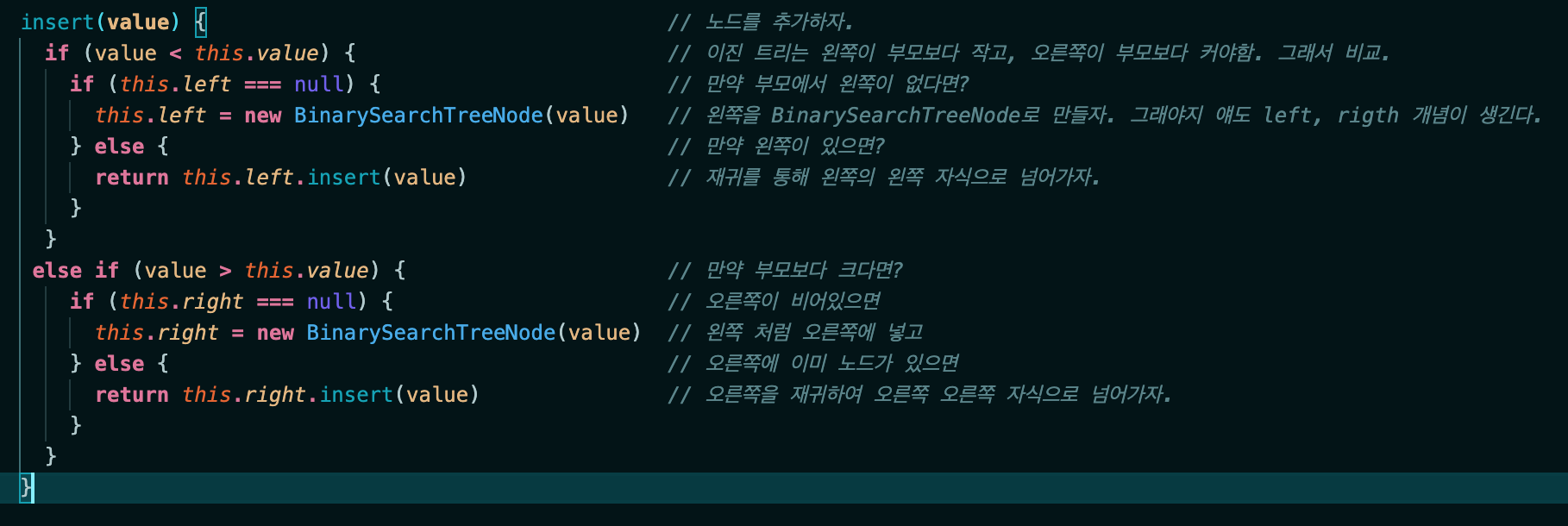
사진이 너무 작은가..
기본적으로 이진트리는 왼쪽 자식이 부모보다 작고, 오른쪽 자식이 부모보다 큰 것을 기억하자!
차근차근
만약 root가 5고 넣고 싶은 값이 3이라면?
1. if (value < this.value) // 이걸 통해 부모보다 값이 작은지 보자
2. if (this.left === null) // 작으면 왼쪽에 노드가 있는지 보자.
3. this.left = new BinarySearchTreeNode(value) //
왼쪽에 자식이 없다면? 바로 왼쪽에 추가!
4. else 그렇지않고 왼쪽에 자식이 있으면??
5. return this.left.insert(value) //
재귀를 통해 왼쪽의 왼쪽 자식으로 넘어가자!
6. 처음부터 반복!
7. 오른쪽은 1~6같은데 left를 right로 바꾸고, 부모보다 큰지 비교하면 된다.insert의 구조를 그림으로 살펴보았다. 1~6번 순서다.
root가 5일 때 3을 넣고 싶다.
6번 그림에서 4를 중심이라고 한 것은 5의 왼쪽 자식인 4를 말하는 것.
3. contains
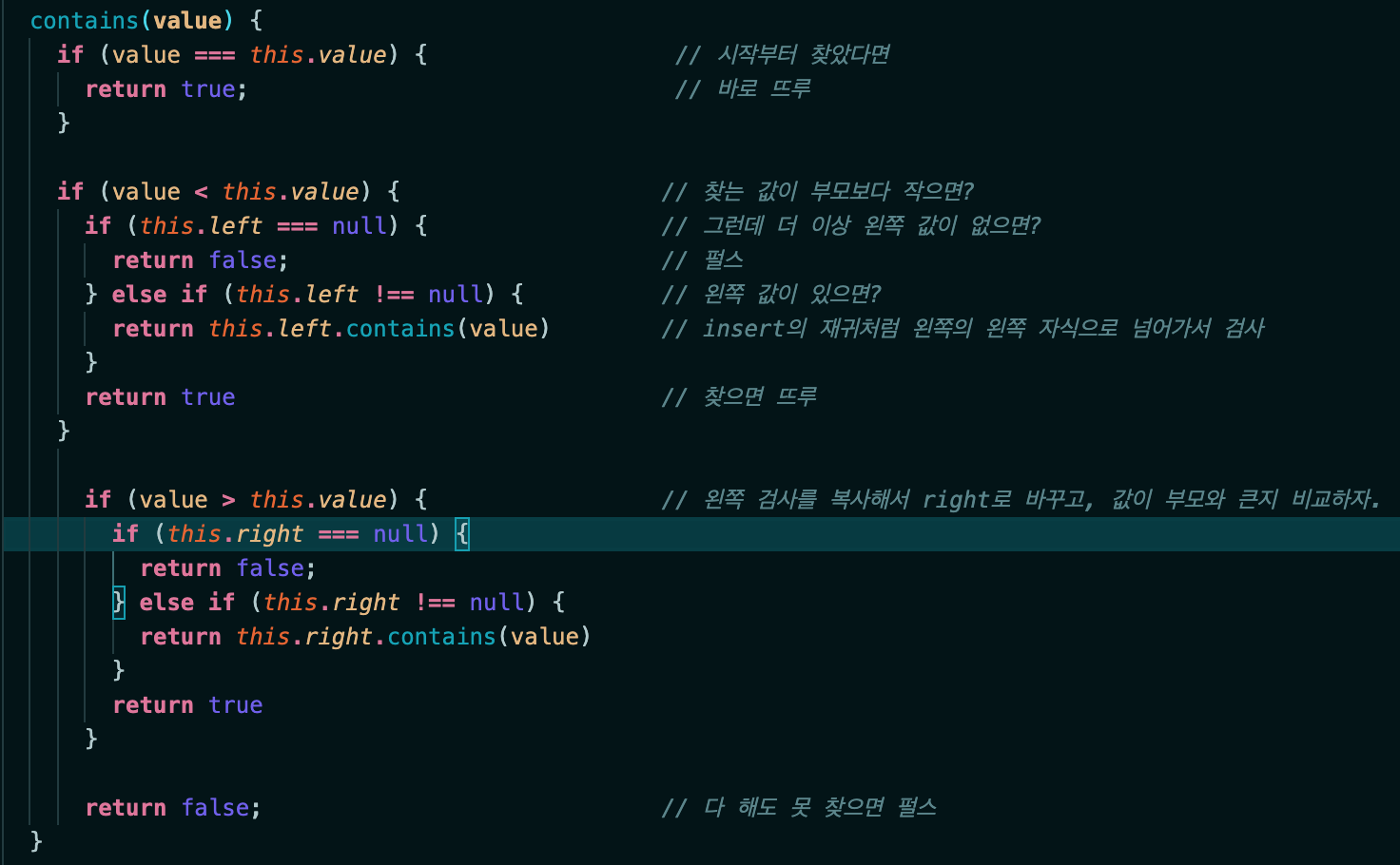
insert와 만드는 것이 비슷하다.
그래서 추가 설명이 없어도 주석을 보고 이해할 수 있을 것 같다.
중요한 것은 재귀를 통해 자식의 자식을 검사하는 것만 이해하면 된다
4. inorder (중위 순회)

중위 순회는 위에 그림으로 설명이 있으니 다시 보고 오자.




ㅎㅅㅎ크리스마스때 나랑 포화 이진트리꾸밀래?
장식은 위에서부터 차례대로 BFS로 순회하면서 다는거야!