JAVA 알고리즘 :: 정렬(2)

📝 정렬

• O(n²)
  • 버블 정렬
  • 선택 정렬
  • 삽입 정렬
• O(n logn)
  • 퀵 정렬
  • 병합 정렬
  • 힙 정렬

💡 퀵 정렬

• 재귀호출을 하는 분할정복 알고리즘
• 정복: 중간 지점의 값을 기준(피봇)으로 삼아 기준보다 작은 값은 앞쪽, 기준보다 큰 값는 뒤쪽에 위치하도록 서로 자리를 바꿈
• 해당 값을 이용해 두 부분으로 범위를 나누어 재귀적으로 또 다시 퀵 정렬을 수행, 그렇게 섹션을 나눠가면서 새로운 피봇을 기준으로 정렬하는 퀵 정렬 과정을 반복하는 방식
• 메모리를 적게 소비
• 재귀를 꼭 사용
• 다른 정렬들에 비해 빠른 속도
• 시간복잡도
  • 평균, O(n logn)
  • O(n²)는 거의 나오지 않으며, 실제 수행에서는 O(n logn)보다 효율이 좋음
• 구현 코드

public static void quickSort(int[] arr, int start, int end) {
    // 소팅 후 정렬이 완료된 시점에 두 섹션을 나누는 뒤쪽 시작점을 반환
    int part2 = partion(arr,start,end);
    
    // 앞쪽 파트 소팅
    if(start < part2-1)
        quickSort(arr, start, part2-1); // 재귀호출
        
    // 뒤쪽 파트 소팅
    if(part2 < end)
        quickSort(arr,part2, end);     // 재귀호출
}

// 정렬 후 나눠지는 두 배열중 뒤쪽 배열의 시작점을 반환
public static int partion(int[] arr, int start, int end)  {
    int pivot = arr[(start+end)/2];
    
    while(start <= end) {   // 피봇값을 기준으로 큰값은 왼쪽 작은값은 오른쪽 정렬됨
        while(arr[start] < pivot) start++;	// 왼쪽 파티션 순회하면서 피봇값과 같거나 큰 경우 swap을 위해 멈춤
        while(arr[end] > pivot) end--;		// 오른쪽 파티션 순회하면서 피봇값과 같거나 작은 경우 swap을 위해 멈춤
        if(start <= end) {  // 서로가 교차되지 않은 경우만 swap
            swap(arr,start,end);
            start++;
            end--;
        } 
        // 서로가 교차된 경우 swap하지 않고 정렬이 다 된 상태
    }
    return start;
}

public static void swap(int[] arr, int a, int b){
	int tmp = arr[a];
	arr[a] = arr[b];
	arr[b] = tmp;
}

💡 병합 정렬

• 분할 정복 알고리즘 기반의 정렬 방식
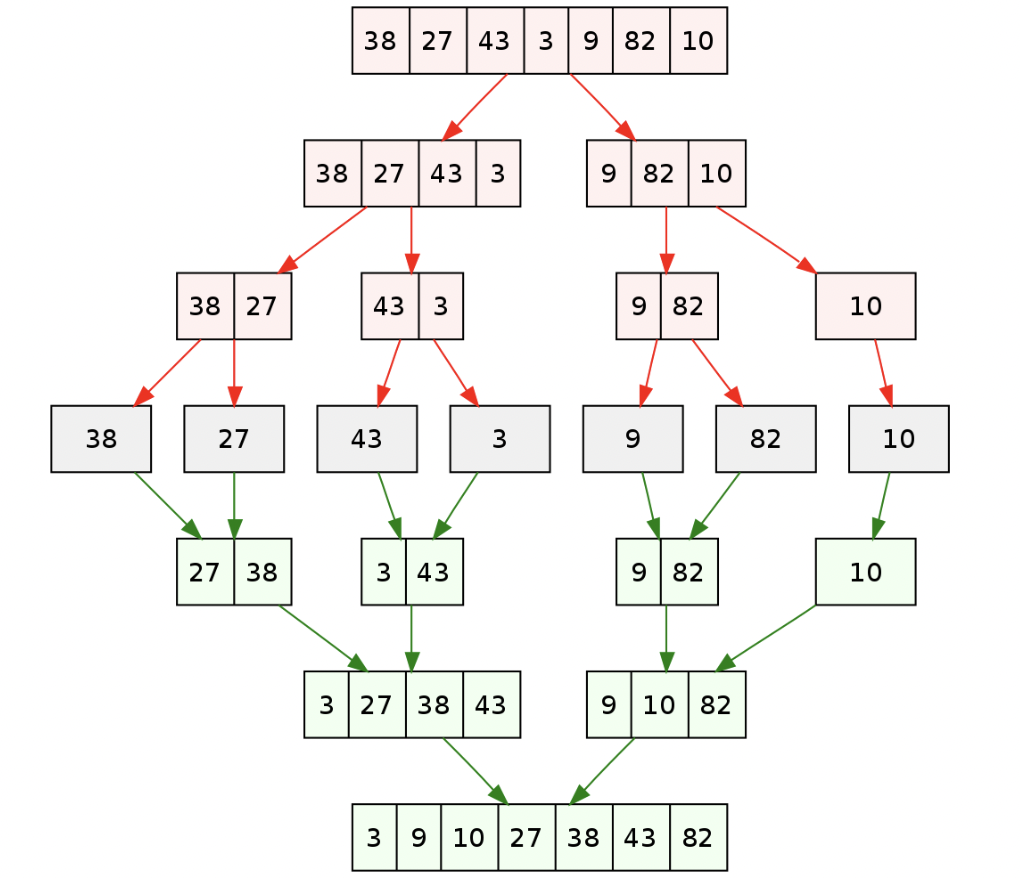
• 길이가 0 또는 1이 아니라면 하나의 리스트를 두 개의 균등한 크기로 분할하고 재귀적으로 여러 리스트로 나누어 각 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 계속해서 합하여 전체가 정렬된 리스트가 되게 하는 방식 ⇝ 정렬해야 할 리스트가 주어지면 해당 리스트를 분할을 반복하여 최대한 작게 쪼개진 시점에 부분리스트에서 인접한 원소들끼리 비교하여 정렬하는 방식
• 병합: 입력 배열을 같은 크기의 2개의 부분 배열로 분할
• 정복: 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용
• 결합: 정렬된 부분 배열들을 하나의 배열에 합병
• 메모리 사용량이 많음
• 데이터가 많을수록 시간이 많이 소요
• 시간복잡도
  • 최악의 경우, O(n logn)

• 구현 코드

// 재귀 사용 시 
public static void mergeSort(int start, int end) {
    if (start < end) {
        int mid = (start + end) / 2;
        mergeSort(start, mid);    // 재귀호출
        mergeSort(mid + 1, end);  // 재귀호출
        int p = start;
        int q = mid + 1;
        int idx = p;
        while (p <= mid || q <= end) {
        // < 이 아닌 이유: 원소의 개수가 1개일 때까지 쪼개기 때문
        // && 이 아닌 이유: 동시에 종료가 되지 않을 수 있기 때문
            if (q > end || (p <= mid && src[p] < src[q])) {
                tmp[idx++] = src[p++];
            } else {
                tmp[idx++] = src[q++];
            }
        }
        for (int i = start; i <= end; i ++) {
            src[i] = tmp[i];
        }
    }
}

// 재귀 미사용 시
public class Merge_Sort {
    private static int[] sorted; // 합치는 과정에서 정렬하여 원소를 담을 임시배열

    public static void merge_sort(int[] a) {
        sorted = new int[a.length];
        merge_sort(a, 0, a.length - 1);
        sorted = null;
    }

    // Bottom-Up 방식 구현
    private static void merge_sort(int[] a, int left, int right) {
        for(int size = 1; size <= right; size += size) {
            for(int l = 0; l <= right - size; l += (2 * size)) {
                int low = l;
                int mid = l + size - 1;
                int high = Math.min(l + (2 * size) - 1, right);
                merge(a, low, mid, high);
            }
        }
    }

    private static void merge(int[] a, int left, int mid, int right) {
        int l = left; int r = mid + 1;
        int idx = left;	// 채워넣을 배열의 인덱스

        while(l <= mid && r <= right) {
            if(a[l] <= a[r]) {
                sorted[idx] = a[l];
                idx++;
                l++;
            } else {
                sorted[idx] = a[r];
                idx++;
                r++;
            }
        }

        if(l > mid) {
            while(r <= right) {
                sorted[idx] = a[r];
                idx++;
                r++;
            }
        } else {
            while(l <= mid) {
                sorted[idx] = a[l];
                idx++;
                l++;
            }
        }

        for(int i = left; i <= right; i++) {
            a[i] = sorted[i];
        }
    }
}

💡 힙 정렬

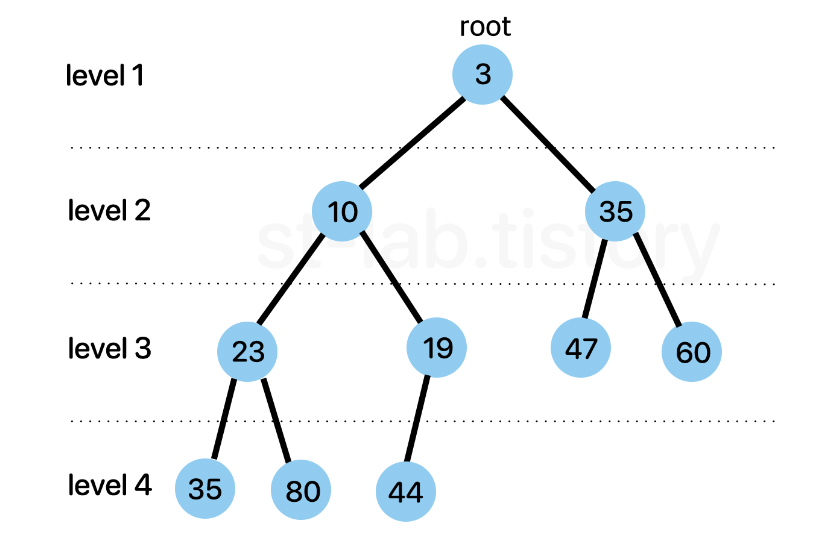
• 힙: 최솟값 또는 최댓값을 빠르게 찾아내기 위해 완전이진트리 형태로 만들어진 자료구조
• 모든 요소들을 고려하여 우선순위를 정할 필요 없이 부모 노드는 자식 노드보다 항상 우선순위가 앞선다는 조건만 만족시키며 완전이진트리 형태로 채워나가는 방식
• 정렬 시 사용하기 좋음
• 시간복잡도
  • 삭제 시, O(logn)
  • 최솟값 혹은 최댓값 찾기, O(1)
  • 최악의 경우, O(n logn)

• 구현 코드

// PriorityQueue collection 사용
PriorityQueue<Integer> heap = new PriorityQueue<Integer>();

// 배열을 힙으로 만든다.
for(int i = 0; i < arr.length; i++) {
    heap.add(arr[i]);
}

// 힙에서 우선순위가 가장 높은 원소(root노드)를 하나씩 뽑는다.
for(int i = 0; i < arr.length; i++) {
    arr[i] = heap.poll();
}

// 직접 구현
public class HeapSort {
    public static void sort(int[] a) {
        sort(a, a.length);
    }

    private static void sort(int[] a, int size) {
        if(size < 2)  // 원소가 1개이거나 0개일 경우
            return;
        
        // 가장 마지막 요소의 부모 인덱스 
        int parentIdx = getParent(size - 1);

        // max heap
        for(int i = parentIdx; i >= 0; i--) {
            heapify(a, i, size - 1);
        }

        for(int i = size - 1; i > 0; i--) {
            swap(a, 0, i);
            heapify(a, 0, i - 1);
        }
    }

    // 부모 인덱스를 얻는 함수
    private static int getParent(int child) {
        return (child - 1) / 2;
    }

    private static void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }

    private static void heapify(int[] a, int parentIdx, int lastIdx) {
        int leftChildIdx; int rightChildIdx; int largestIdx;

        while((parentIdx * 2) + 1 <= lastIdx) {
            leftChildIdx = (parentIdx * 2) + 1;
            rightChildIdx = (parentIdx * 2) + 2;
            largestIdx = parentIdx;

            if (a[leftChildIdx] > a[largestIdx]) 
                largestIdx = leftChildIdx;

            if (rightChildIdx <= lastIdx && a[rightChildIdx] > a[largestIdx]) 
                largestIdx = rightChildIdx;

            if (largestIdx != parentIdx) {
                swap(a, parentIdx, largestIdx);
                parentIdx = largestIdx;
            } else 
                return;
        }
    }
}