내일배움캠프 TIL - 부동소수점

Jaden Lee·2025년 4월 17일

내일배움캠프

목록 보기

13/15

💡 부동소수점(Floating Point)이란?

컴퓨터는 실수를 정확하게 저장하기 어렵습니다. 왜냐하면 10진수의 소수를 2진수로 바꿀 때, 정확하게 표현되지 않는 수가 많기 때문입니다. 예를 들어 0.1은 2진수로 정확하게 표현되지 않습니다. 그래서 컴퓨터는 실수를 저장할 때 부동소수점(Floating Point) 방식으로 근사해서 저장합니다.

부동소수점은 IEEE 754 표준에 따라 다음과 같이 표현됩니다:

부호(Sign) : 1비트
지수부(Exponent) : 8비트 (단정도) / 11비트 (배정도)
가수부(Fraction) : 23비트 (단정도) / 52비트 (배정도)
예를 들어, float(32bit)는 대략 7자리 십진수 정확도, double(64bit)은 약 15~16자리 정확도를 제공합니다.

부동소수점 예시

−118.625 (십진법)을 IEEE 754 (32비트 단정밀도)로 표현해 보자.

음수이므로, 부호부는 1이 됩니다.
그 다음, 절댓값을 이진법으로 나타내면 1110110.101이 됩니다. (이진기수법을 참조)
소수점을 왼쪽으로 이동시켜, 왼쪽에는 1만 남게 만듭니다. 예를 들면 1110110.101=1.110110101×2⁶ 과 같습니다. 이것을 정규화된 부동소수점 수라고 합니다.
가수부는 소수점의 오른쪽 부분으로, 부족한 비트 수 부분만큼 0으로 채워 23비트로 만듭니다. 결과는 11011010100000000000000이 됩니다.
지수는 6이므로, Bias를 더해야 합니다. 32비트 IEEE 754 형식에서는 Bias는 127이므로 6+127 = 133이 됩니다. 이진법으로 변환하면 10000101이 됩니다.
이 결과를 정리해서 표시하면 다음과 같습니다.

⚠️ 부동소수점의 문제점

부동소수점의 근사 표현 방식 때문에 다음과 같은 문제가 발생할 수 있습니다:

정밀도 손실

0.1 + 0.2 != 0.3 → 부동소수점 연산 결과는 0.30000000000000004

비교 오류

a == b 비교가 항상 참이 아님

누적 오차

반복 연산 또는 누적 시 오차가 커짐

플랫폼 간 차이

부동소수점 연산이 하드웨어/언어별로 달라질 수 있음

💥 실제 사례 - 패트리어트 미사일 실패

미사일요격시스템 패트리어트

1991년 걸프전, 미군의 패트리어트 미사일 시스템이 이라크 스커드 미사일을 격추하지 못한 사건이 있었습니다. 그 이유는 바로 부동소수점 오차 때문이었습니다.
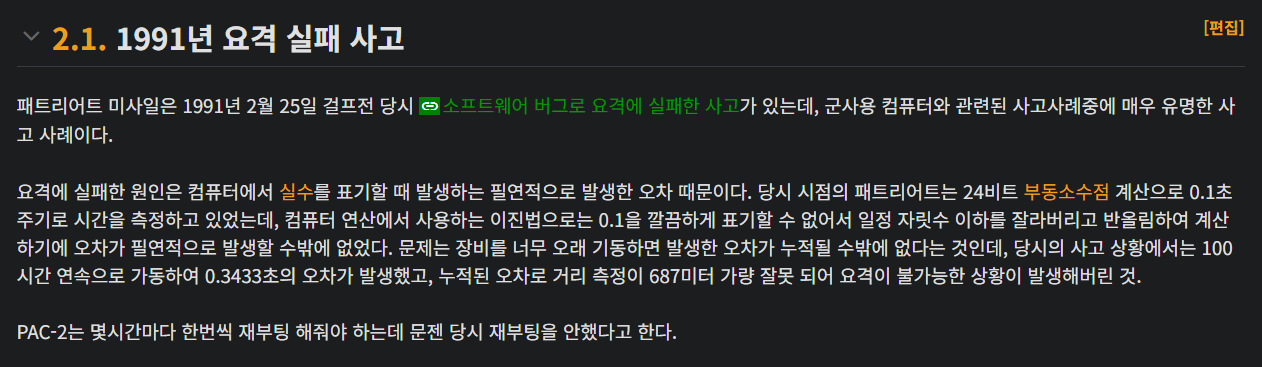
나무위키 발췌

사건 개요

미사일 추적 시스템은 시간을 tick(=0.1초) 단위로 저장
tick * 1/10을 통해 실제 시간 계산
1/10을 2진수로 표현하면 무한소수 (0.0001100110011...)
시스템은 이를 24비트만 사용하여 근사 → 시간이 지날수록 오차 누적
100시간 작동 후, 약 0.34초 시간 오차 발생
스커드 미사일은 0.34초에 500m 이상 이동 가능 → 격추 실패

핵심

작은 오차도 누적되면 치명적인 결과를 초래할 수 있다

🛠️ 해결 방법 (Flutter 예제 포함)

부동소수점 오차를 줄이기 위한 대표적인 방법은 다음과 같습니다:

✅ 1. 정수로 처리하기 (소수점 대신 정수 단위 관리)

금액, 거리 등 단위를 고정할 수 있는 경우에는 정수형으로 처리하는 것이 좋습니다.

// Flutter 예제 - 금액을 cents 단위로 처리
int priceA = 1500; // $15.00
int priceB = 299;  // $2.99

int total = priceA + priceB;
print('Total in cents: $total'); // 1799
print('Total in dollars: \$${(total / 100).toStringAsFixed(2)}'); // $17.99

✅ 2. 오차 허용 범위 설정 (epsilon)

비교 시 정확한 일치 대신 허용 오차(Epsilon) 범위를 둡니다.

// Flutter 예제 - 부동소수점 비교
bool isAlmostEqual(double a, double b, [double epsilon = 0.00001]) {
  return (a - b).abs() < epsilon;
}

void main() {
  double x = 0.1 + 0.2;
  double y = 0.3;

  print('x: $x'); // 0.30000000000000004
  print('isAlmostEqual: ${isAlmostEqual(x, y)}'); // true
}

✅ 3. 고정소수점 라이브러리 사용

Dart에서는 decimal 패키지처럼 정확한 수치 연산이 가능한 라이브러리를 사용할 수 있습니다.

import 'package:decimal/decimal.dart';

void main() {
  Decimal a = Decimal.parse('0.1');
  Decimal b = Decimal.parse('0.2');
  Decimal c = a + b;

  print('Result: $c'); // 0.3
}