🆚 DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색)의 비교
DFS(Depth First Search)는 특정 노드에서 시작해, 인접한 노드 중 방문하지 않은 노드를 따라 가능한 한 깊게 탐색하는 알고리즘이다. 더 이상 진행할 수 없는 지점에 도달하면 이전 지점으로 되돌아가며 다른 경로를 탐색한다. DFS는 방문한 노드를 다시 방문하지 않기 위해 visited 배열/집합을 사용하며, 구현은 보통 재귀 호출 또는 스택(Stack)을 이용한다.
BFS(Breadth First Search)는 특정 노드에서 시작해, 현재 깊이(거리)의 모든 노드를 먼저 탐색한 뒤 다음 깊이로 이동하는 알고리즘이다. BFS는 큐(Queue)를 사용하며, 방문한 노드를 다시 방문하지 않기 위해 visited를 사용한다. 특히 간선 가중치가 모두 동일한 그래프에서는 시작점으로부터의 최단 거리(최소 이동 횟수)를 보장하기 때문에 최단 경로 문제에서 자주 활용된다.
정리하면 DFS는 “한 경로를 끝까지 파고든 뒤 되돌아오며 탐색하는 방식”, BFS는 “가까운 노드부터 차례대로 넓게 퍼져나가며 탐색하는 방식” 이라고 생각하면 편하다.
🤔 왜 DFS, BFS 같은 탐색 알고리즘을 배워야 할까?
DFS와 BFS는 그래프에서 연결된 모든 경우의 수를 탐색하는 가장 원초적인 방법이다. 현실의 많은 문제는 결국 노드와 간선으로 표현할 수 있기 때문에, 탐색 알고리즘을 알면 복잡해 보이는 문제도 그래프로 모델링하고 탐색해서 해결할 수 있다.
특히 DFS와 BFS는 다른 심화된 알고리즘의 기반이 된다. 예를 들어, 최단 경로(다익스트라), 위상 정렬, 사이클 탐지, 연결 요소 개수 세기, 트리 순회, 미로 탐색 같은 문제들이 모두 DFS나 BFS와 연결되어 있다. 즉 DFS와 BFS를 잘 이해하고 있으면 단순히 탐색만 하는 것이 아닌, 문제를 구조화하고 해결하는 사고력 자체가 크게 향상될 것이다.
간단하게 각 알고리즘이 쓰이는 상황을 나열하자면,
DFS가 많이 쓰이는 상황- 모든 경로 탐색(경로가 존재하는지, 가능한 경우의 수)
- 백트래킹이나 완전 탐색(순열, 조합, N-Queen, 스도쿠 등)
- 트리나 그래프 순회
- 사이클 판별, 연결 요소 탐색
BFS가 많이 쓰이는 상황- 최단 거리나 최소 이동 횟수를 구할 때(간선 가중치가 동일해야 함)
- 레벨 단위 탐색(거리가 1, 2, 3 …)
- 미로 최단 거리 탈출, 최소 버튼 누르기, 최소 시간 등
가능한 경우를 깊게 들어가서 확인해야 한다면 DFS, 가장 빠르게 혹은 최소 횟수라는 키워드가 있다면 BFS가 옳은 선택인 경우가 많다.
🛠 DFS(Depth First Search) 분석
1번 노드에서 시작한다고 했을 때, 1번 노드가 갈 수 있는 선택지는 왼쪽, 가운데, 오른쪽이 있다. 여기서 왼쪽에 있는 노드에서 갈 수 있는 끝까지를 찍고 나서 가운데, 오른쪽으로 차례대로 간다는 것이다.
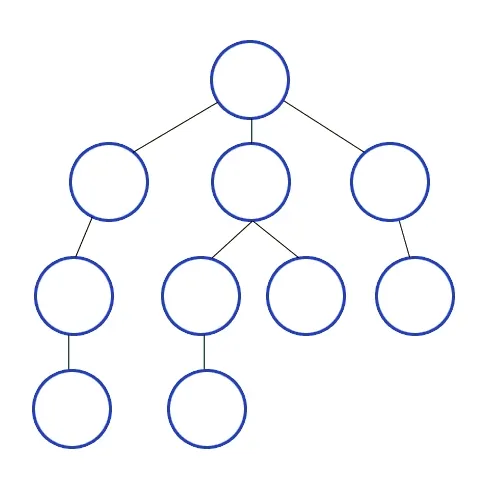
구체적으로 실행 과정을 요약해보자면, 노드를 방문하고, 깊이 우선으로 인접한 노드를 방문하고, 또 그 노드를 방문해서 깊이 우선으로 인접한 노드를 방문한다. 만약 끝까지 갔다면 리턴한다는 정도로 말할 수 있다.
DFS의 반복 방식은 아래와 같이 방문하지 않은 원소를 계속해서 찾아가면 된다. 방문하지 않았다는 조건은 visited와 같은 배열에 방문한 노드를 일일이 기록해주면 된다.
DFS(노드 A) = 노드 A + DFS(노드 A와 인접하지만 방문하지 않은 다른 노드)
이제 DFS를 구현해보도록 하자.
- 루트 노드부터 시작한다.
- 현재 방문한 노드를
visited에 추가한다. - 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 방문한다.
- 2번 과정부터 반복한다.
🍕 DFS 재귀 구현
package org.dfs;
import java.util.ArrayList;
import java.util.List;
public class DfsRecursive {
static List<Integer>[] adjList;
static boolean[] visited;
static void dfs(int node) {
visited[node] = true;
System.out.println("Visited node: " + node);
for (int nextNode : adjList[node]) {
if (!visited[nextNode]) {
dfs(nextNode);
}
}
}
public static void main(String[] args) {
int n = 10;
int[][] edgeInfo = {
{1, 2}, {1, 5}, {1, 9}, {2, 3}, {3, 4},
{5, 6}, {6, 7}, {5, 8}, {9, 10}
};
adjList = new ArrayList[n + 1];
visited = new boolean[n + 1];
for (int i = 1; i <= n; i++) {
adjList[i] = new ArrayList<>();
}
for (int[] info : edgeInfo) {
adjList[info[0]].add(info[1]);
adjList[info[1]].add(info[0]);
}
dfs(1);
}
}
/**
* Visited node: 1
* Visited node: 2
* Visited node: 3
* Visited node: 4
* Visited node: 5
* Visited node: 6
* Visited node: 7
* Visited node: 8
* Visited node: 9
* Visited node: 10
*/하지만, 재귀를 통해서는 무한정 깊어지는 노드가 있는 경우 에러가 발생할 수 있다. 이 문제를 피하기 위해 다른 방법을 강구해야 한다. DFS는 탐색하는 원소를 최대한 깊게 따라가야 하는데, 이걸 다시 말하면 인접한 노드 중 방문하지 않은 모든 노드들을 저장해두고, 가장 마지막에 넣은 노드들만 꺼내서 탐색하면 된다는 것이다. 이때 스택을 사용하는 것이다.
구현 순서는 아래와 같다.
- 루트 노드를 스택에 넣는다.
- 현재 스택의 노드를 빼서
visited에 추가한다. - 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 스택에 추가한다.
- 2번 과정부터 반복한다.
- 스택이 비면 탐색을 종료한다.
🥞 DFS 스택 구현
package org.dfs;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
public class DfsStack {
static List<Integer>[] adjList;
static boolean[] visited;
static void dfs(int start) {
Deque<Integer> stack = new ArrayDeque<>();
stack.push(start);
while (!stack.isEmpty()) {
int node = stack.pop();
if (visited[node]) {
continue;
}
visited[node] = true;
System.out.println("Visited node: " + node);
for (int next : adjList[node]) {
if (!visited[next]) {
stack.push(next);
}
}
}
}
public static void main(String[] args) {
int n = 10;
int[][] edgeInfo = {
{1, 2}, {1, 5}, {1, 9}, {2, 3}, {3, 4},
{5, 6}, {6, 7}, {5, 8}, {9, 10}
};
adjList = new ArrayList[n + 1];
visited = new boolean[n + 1];
for (int i = 1; i <= n; i++) {
adjList[i] = new ArrayList<>();
}
for (int[] info : edgeInfo) {
adjList[info[0]].add(info[1]);
adjList[info[1]].add(info[0]);
}
dfs(1);
}
}
/**
* Visited node: 1
* Visited node: 9
* Visited node: 10
* Visited node: 5
* Visited node: 8
* Visited node: 6
* Visited node: 7
* Visited node: 2
* Visited node: 3
* Visited node: 4
*/
⚒ BFS(Breadth First Search) 분석
최대한 깊게 따라가야 하는 DFS와 다르게, BFS는 현재 인접한 노드(들)를 먼저 방문해야 한다. 이걸 다시 말하면 인접한 노드 중 방문하지 않은 모든 노드들을 저장해두고, 가장 처음에 넣은 노드를 꺼내서 탐색하면 된다.
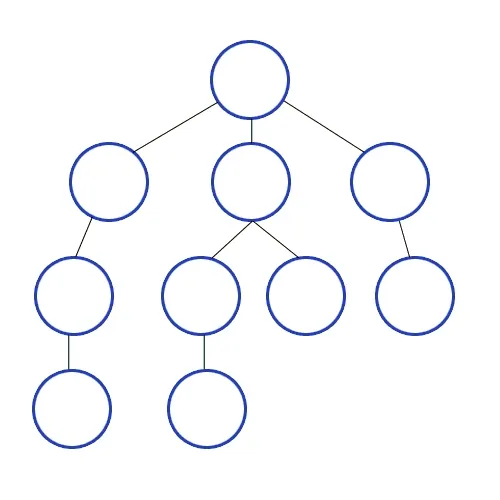
구현 순서는 아래와 같다.
- 루트 노드를 큐에 넣는다.
- 현재 큐의 노드를 빼서
visited에 추가한다. - 현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 큐에 추가한다.
- 2번 과정부터 반복한다.
- 큐가 비면 탐색을 종료한다.
🍡 BFS 큐 구현
package org.bfs;
import java.util.*;
public class Bfs {
static List<Integer>[] adjList;
static boolean[] visited;
static void bfs(int start) {
Deque<Integer> queue = new ArrayDeque<>();
queue.offer(start);
visited[start] = true;
while (!queue.isEmpty()) {
int node = queue.poll();
System.out.println("Visited node: " + node);
for (int next : adjList[node]) {
if (!visited[next]) {
visited[next] = true;
queue.offer(next);
}
}
}
}
public static void main(String[] args) {
int n = 10;
int[][] edgeInfo = {
{1, 2}, {1, 3}, {1, 4}, {2, 5}, {3, 6},
{3, 7}, {4, 8}, {5, 9}, {6, 10}
};
adjList = new ArrayList[n + 1];
visited = new boolean[n + 1];
for (int i = 1; i <= n; i++) {
adjList[i] = new ArrayList<>();
}
for (int[] info : edgeInfo) {
adjList[info[0]].add(info[1]);
adjList[info[1]].add(info[0];
}
bfs(1);
}
}
/**
* Visited node: 1
* Visited node: 2
* Visited node: 3
* Visited node: 4
* Visited node: 5
* Visited node: 6
* Visited node: 7
* Visited node: 8
* Visited node: 9
* Visited node: 10
*/
