[Causal Inference] Graphical Causal Models

안녕하세요! 오늘 다뤄볼 주제는 Graphical Causal Models입니다. 제가 전공하였던 분야이기도합니다! 저는 데이터를 통해 이러한 그래피컬 모델을 추정하는 방법에 대해 공부를 하였었는데요! 지난 학생동안 공부했던것을 복습하며 정리해보겠습니다.

Thinking About Causality

Grahical model은 인과 관계의 언어입니다. 인과관계를 논할때 소통의 매개체가 되기도하고 생각을 조금 더 명확하게 나타내기 쉽기도합니다. 또한 개인적인 생각이지만 Graphical model에 대한 이해는 인과관계를 바라볼때 조금 더 명확하게 바라볼 수 있고 이를 해석하기 쉽게 해준다고 생각합니다!!

우선, 잠재 결과의 조건부 독립관계를 살펴보면서 시작하겠습니다. 인과관계 추론에서 필요한 주요한 가정중 하나입니다.
$(Y_0, Y_1) \perp T \mid X$

어떠한 변수 X를 조건으로 가지면서 Treatment와 잠재적 결과가 독립이 되게 함으로써 Treatment에 대한 인과 효과를 추정할 수 있습니다.

Example ) 중증환자에 대한 약물의 영향

중증환자에게만 약을 투여할 경우에 약물의 투약이 건강을 악화시키는 것 처럼 해석될 수 있습니다.
하지만 중증환자와 그렇지 않은 환자를 분류하고 각 그룹에서 약물의 영향을 분석하면 약물의 효과를 더욱 명확하게 알아 볼 수 있습니다. 이러한 조건화를 통해 Treament가 무작위하게 적용된 것처럼 나타내어질 수 있고 (조건부 독립성), 이를 통해 Treatment의 효과를 올바르게 추정할 수 있습니다.

이러한 조건부 독립관계는 인과관계 추론의 핵심이지만, 이를 상상하거나 생각하는 것은 다소 어렵게 느껴집니다..! 그렇기 때문에 인과관계를 표현할 수 있는 언어가 필요하고, 이 언어가 오늘 다루게 될 Causal Graphical Model 입니다

그래피컬 모델에 대해 간단히 소개해보면,

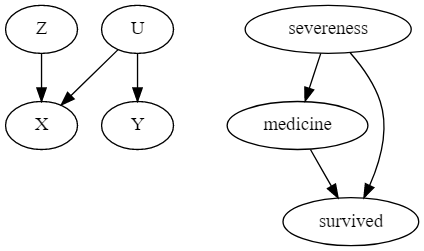
각 노드는 확률 변수를 가지며, 변수가 다른 변수에 영향을 주는지 나타내기 위해 엣지(화살표)를 이용하여 나타냅니다. 왼쪽의 그래프는 Z가 X에 영향을 미치고, U가 X와 Y에 영향을 미치는 것을 나타내고 있습니다. 구체적인 예시를 들어보면 오른쪽의 그래프와 같이 환자 생존에 대한 약의 영향을 해석해볼 수 있습니다! 병증이 심각하면 약물 투약을 하게 되고, 생존에도 영향을 미칩니다. 그리고 약물 투약도 생존의 원인이 되겠죠!

Crash Course in Graphical Models

그래피컬 모델에서 나타나는 몇가지 조건부 독립가정을 이해하기 위해 몇 가지 유형의 조건부 독립형태를 알아보겠습니다!

Mediater 형태

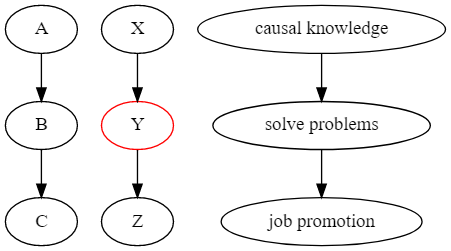
이 그래프에서 A는 B에 영향을 주고, B는 C에 영향을 미치고 있습니다. 마찬가지로 X는 Y에 영향을 미쳐 Z에 영향을 미치게 됩니다.

각 그래프에서 종속성/영향력은 화살표 방향의 방향을 따라 전달됩니다. 가장 오른쪽의 그래프와 함께 구체적인 예를 들어보겠습니다!

인과관계에 대한 지식이 어떠한 문제해결의 유일한 방법이고 이러한 문제해결이 승진을 위한 유일한 방법이라고 가정해 보겠습니다. 여기서 인과관계에 대한 지식이 문제를 해결할 수 있게 도와주고 이를 통해 승진할수 있게 됩니다. 여기서 우리는 승진이 인과관계에 대한 지식에 좌우된다고 말할 수 있습니다. 이러한 종속성은 다소 직관적이지 않지만 대칭적으로 나타납니다. 승진 가능성이 높을수록 인과관계에 대한 지식을 보유하고 있을 가능성이 높아집니다.
$\;$
여기서 중간에 위치한 변수를 조건화 해보겠습니다. 이 경우 종속성이 끊어지게 되어 X와 Z는 Y가 주어지면 독립적입니다. 마찬가지로, 위의 예시에서 어떠한 사람이 문제해결능력을 가지고 있다는 것을 아는 경우, 인과관계 지식 보유 여부는 승진 기회에 대한 더 이상 어떠한 정보도 가지지 않게 됩니다.

이것을 수학기호를 통해 나타내보면 다음과 같이 나타납니다!

$Causal\;Knowledge\not\perp Job\; Promotion$

$Causal\;Knowledge\perp Job\; Promotion \mid Solve\; Problem$

Confounder 형태

이 형태의 그래프에서는 동일한 변수로 인해 두 개의 다른 변수가 영향을 받게 됩니다. 이 형태에서 종속성은 화살표를 통해 거꾸로 발생하게 되어 백도어 경로가 발생합니다. 여기서 두 변수에 영향을 주는 하나의 변수를 조건화하면 종속성을 없엘 수 있게됩니다.

예를 들어 통계학적 지식이 인과 추론과 기계 학습에 대한 이해도를 높일 수 있다고 가정해보겠습니다! 통계학적 지식 수준을 모르는 경우에, 인과 추론에 능숙하다는 정보를 통해 기계 학습에도 능숙할 가능성이 높다는 것을 알 수 있게됩니다. 통계학적 지식 수준을 모른다 하더라도 높은 인과 추론 지식을 통해 통계학적 지식 수준이 높음을 추론이 가능하기 때문입니다!
$\;$
통계학적 지식 수준을 알고있는 경우에 머신 러닝 지식과 인과 추론 지식은 무관하게 됩니다. 통계학적 지식 수준은 머신러닝 지식 수준을 추론하는 데 필요한 모든 정보를 제공하며, 인과관계 추론 지식또한 마찬가지 입니다. 즉, 이러한 경우에 인과 관계 추론 지식수준을 아는 것이 머신러닝 지식수준에 대한 정보를 줄 수 없습니다.

이것을 수학기호를 통해 나타내보면 다음과 같이 나타납니다!

$Causal\;Inferendce\not\perp Machine\; Learning$

$Causal\;Inferendce\perp Machine\; Learning \mid Statistics$

Collider 형태

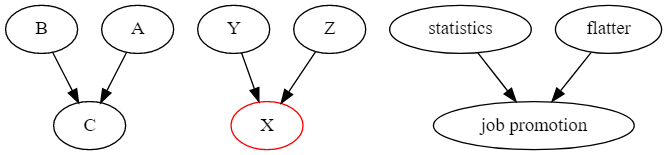
이 유형은 두 개의 엣지가 하나의 변수에서 만나는 유형입니다. 이 경우 두 변수가 공통된 변수에 각각 효과를 전달하는 구조를 가지고 있습니다.

승진하는 방법에는 두 가지가 있다고 가정해보겠습니다! 어떠한 직원이 통계학에 능숙하거나 아첨을 잘 할 수 있습니다. 만약 승진 여부를 알지 못할 때, 통계학 수준과 아첨을 잘하는지에 대한 여부는 서로 독립적으로 나타날 것입니다. 하지만 승진을 했다는 사실을 아는 경우에, 통계학 지식 수준을 알면 아첨을 잘하는지 못하는지 어느정도 알 수 있게됩니다. 통계학에 능숙하고 승진을 했다면 아첨에 대한 수준을 알게 될 가능성이 높아집니다. 반대로 아첨에 서툴다는 사실을 안다면 통계학에 아주 능숙할 가능성이 매우 높습니다. 이러한 현상은 하나의 원인이 이미 결과를 어느정도 설명하고 있고 다른 원인에 대한 어떠한 가능성이 줄어들기 때문입니다.

이것을 수학기호를 통해 나타내보면 다음과 같이 나타납니다!

$Statitics \perp Flatter$

$Statitics \not\perp Flatter\mid Job\;Promotion$

Markov Equivalence Class

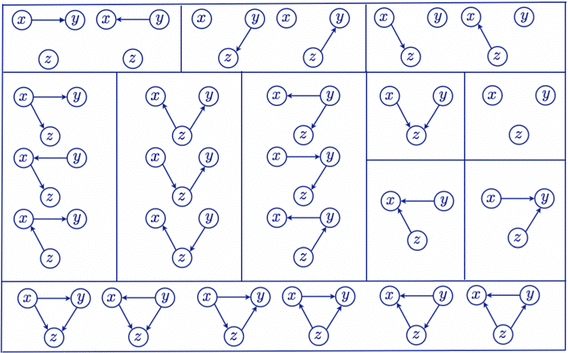
마지막으로 MEC에 대해 간략하게 설명드리겠습니다. 위 그림은 어떠한 3개의 변수가 존재할 때에 가능한 DAG에서 동일한 조건부 독립관계를 가지는 DAG들을 묶어 놓은 그림입니다! 여기서 특이하게도 Collider형태의 DAG는 유니크한 조건부 독립관계를 보여주고있는데요! 저희는 이를 통해서 조건부 독립관계만 알더라도 어느정도 인과관계를 추론해볼 수 있으며, 특히 Collider 구조는 유니크하게 나타나기때문에 식별이 가능합니다!

상관관계가 인과관계를 말하지는 않지만, 상관관계를 통해 인과관계를 부분적으로 알 수 있음을 보여주는 예시라고 볼 수 있을 것 같습니다!

Confounding Bias

인과관계 추론에 있어 몇가지 이유가 있는데 이중 가장 큰 원인은 Confounder구조 입니다. 즉, Treatment와 결과가 공통된 원인을 공유하게 될 때 발생하게됩니다!

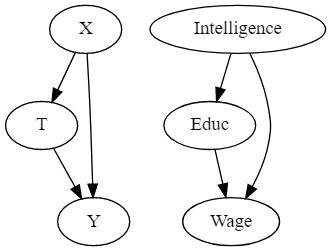
예를 들어 Treament가 교육이고 결과가 소득이라고 해보겠습니다. 둘 다 지능이라는 공통된 원인을 가지기 때문에 때문에 임금에 대한 교육의 인과적 영향을 알기는 어렵습니다. 많은 교육을 받은 사람들이 교육을 더 많이 받았기 때문이 아니라 지능이 높기 때문에 높은 임금을 받는다고 주장할 수 있기 때문입니다. 인과관계를 정확히 추정하기 위해서 Treatment와 결과 사이에 나타나는 백도어 경로를 차단해야 합니다. 그렇게 되면 T->Y로의 직접적인 효과만이 남게 됩니다. 예시에서 지능을 통제한다면, 즉 지능 수준은 같지만 교육 수준이 다른 사람들을 비교한다고 할 때 결과의 차이는 교육의 차이만을 이용하여 설명 가능하게 됩니다. 즉, 이러한 Confouding Bias를 조정하기 위해 Confounder를 통제해야 합니다.

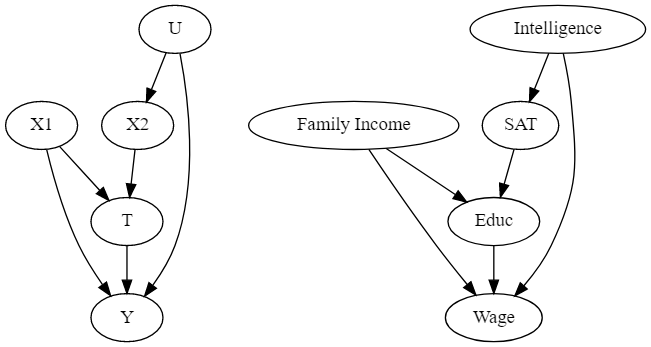
하지만 모든 공통 원인을 통제하는 것은 현실적으로 불가능 할 수도 있습니다! 때로는 알 수 없는 원인이나 측정할 수 없는 알려진 원인이 있습니다. 지능의 경우 IQ라는 지표가 있긴하지만 아직도 지능을 확실하게 측정하는 것은 쉬운일이 아닙니다..! 여기서 지능이 교육에 직접적인 영향을 주지 않는다고 잠깐 가정해보겠습니다. 지능은 SAT와 같은 수학능력시험에 대한 성적에 영향을 미치기는 하지만, 좋은 대학을 가기 위한 가능성을 열어주는 것은 SAT이기 때문에 교육 수준을 결정하는 것은 SAT입니다.

• 지능이 측정이 어려워 이를 제어하기 어렵더라도 SAT를 제어함으로써 백도어 경로를 차단할 수 있습니다.

위 그래프에서 X1 및 X2, 또는 SAT 및 가족 소득에 대한 조건화를 통해 Treatment와 결과 사이의 백도어 경로를 차단할 수 있습니다. 따라서, 공통된 원인을 측정할 수 없더라도 치료에 대한 측정되지 않은 영향을 매개하고 있는 다른 측정 가능한 변수를 통제함으로써 조건부 독립성을 확보할 수 있습니다!

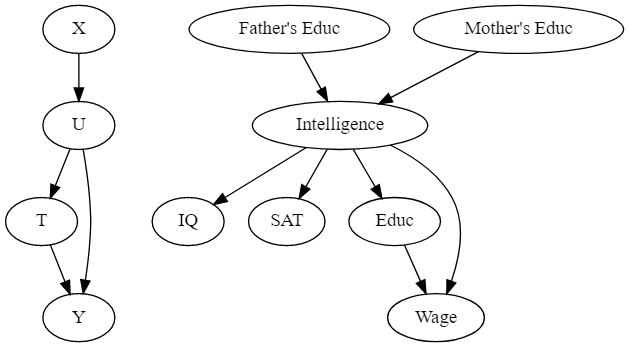
하지만 그것 조차도 불가능한 상황에는 어떻게 해야할까요? 측정되지 않은 변수가 치료와 결과를 직접적으로 유발한다면 어떻게 될까요? 위 그래프에서는 지능은 교육과 수입에 직접적으로 영향을 미치고 있습니다. 따라서 교육과 임금 간의 관계에 어떠한 혼란을 유발하게 됩니다! 이 경우 Confounder(지능)은 측정할 수 없기 때문에 직접적으로 제어할 수 없습니다.

여기서 이러한 Confounder를 측정할 수 있는 다른 변수를 이용할 수 있습니다. 이러한 변수를 이용해 백도어 경로를 완벽히 차단할 수 없지만 이를 제어함으로써 편향을 크게 낮출 수 있다고 합니다. 예시에서는 지능을 측정할 수 없지만 아버지와 어머니의 교육과 같은 몇 가지 원인과 IQ 또는 SAT 점수와 같은 몇 가지 영향을 측정할 수 있습니다. 이러한 대리 변수를 제어하는 것은 편향을 제거하는 데 충분하지 않지만 큰 효과를 보인다고 합니다!!

Selection Bias

다음으로 이야기해볼 것은 선택편향인데요! 위에서 공통된 원인이 되는 변수를 제어하지 않은 경우에 교란편향이 발생하지만 선택편향을 조금 반대되는 상황에서 발생합니다. 왜냐하면 선택편향은 실제로 너무 많은 변수를 통제함으로써 나타나기 때문인데요! 이에 대해 알아보겠습니다.

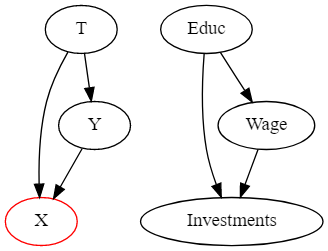
교육이 임금에 미치는 영향을 측정하기 위해 무작위로 교육수준을 조절했다고 가정해보겠습니다. 위에서 배웠던 것과 같이 교란편향을 없에기 위해 많은 변수를 제어해야 합니다. 그 중 투자금액을 통제한다고 해보겠습니다. 투자금액은 교육수준과 임금의 공통된 결과인데요. (교육을 많이 받은 사람들은 더 많은 임금을 받고 더 많이 투자한다고 가정하겠습니다.) 여기서 투자금액은 Collider이기 때문에 이를 조건으로 가질 경우에 교육수준과 임금 사이에 다른 종속성이 생겨 직접적인 효과를 추정하기 어려워집니다.

설명하기 쉽게 투자금액과 교육이 이진변수라고 가정해보겠습니다. 어떠한 사람이 투자하든 말든 교육을 받았든 안 받았든. 처음에 투자를 통제하지 않을 때 편향 항은 0입니다.

$E[Y_0 \mid T =1 ] - E[Y_0\mid T=0 ] = 0$

교육이 무작위로 제어되었기 때문입니다! 하지만 여기서 만약 투자를 제어한다면,

$E[Y_0 \mid T= 0, I= 0] > E[Y_0 \mid T= 0, I= 1]$

으로 편향이 발생하게 됩니다. 간단하게 생각해보면 교육수준이 낮으면서 투자를 하지 않은 경우 임금이 낮을 가능성이 높고, 교육수준이 낮으면서 투자를 한 경우 임금이 높은 가능성이 높기 때문입니다!

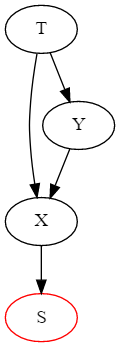
위 그림처럼 앞선 예와 비슷한 경우에서, Collider의 자식(child)를 조건으로 할때에도 위와 거의 유사한 일이 발생하기 때문에 이러한 상황에도 선택편향이 발생합니다.

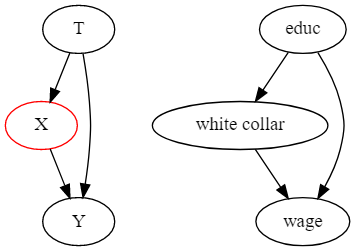
우리가 Treatment의 mediator를 조건으로 삼을 때도 비슷한 발생합니다. 예를 들어, 교육수준을 무작위로 제어하였다고 가정해보겠습니다. 여기서 또한 그 사람이 화이트 칼라 직업을 가지고 있는지 여부를 제어한다고 하여봅시다. 이때 이러한 조건화는 인과 관계 추정에 편향을 발생시킵니다. 이번에는 Collider를 통해 다른 종속성을 발생시킨 것이 아니라, Treament의 효과가 전달되는 채널 중 하나를 닫았기 때문입니다. 위 예에서 화이트 칼라 직업을 갖게 되는 것은 더 높은 교육수준이 더 높은 임금으로 이어지는 어떠한 방법중 하나입니다. 이를 통제함으로써 우리는 이 채널을 닫고 교육수준이 임금에 미치는 직접적인 영향만 허용하게 됩니다.