Introduction

GCN(Graph Convolution Network)에 대하여 개인적으로 공부한 부분을 토대로 기술합니다.
GCN을 이해하기 위한 기초적인 개념부터, G / C / N 각각이 무엇을 뜻하는지 학습합니다.

데이터의 표현 방식

DATA representataion 즉, 데이터의 표현방식에 대해서 먼저 알아보겠습니다.

이미지의 데이터는 일반적인 영상데이터로 2차원 평면에 그려진 시각적으로 표현되는 그래프는 각 픽셀마다 해당 픽셀에 밝기값, 투명도 등 여러 데이터가 존재합니다.

이러한 이미지는 주로 CNN방식으로 분류하게 됩니다.

반면 시계열 데이터는 말 그대로 시간 별로 구성된 집합으로 음성이나 자연언어, 센서 데이터, 주가 등의 데이터를 나타내는데, 이는 주로 RNN방식으로 분류하게 됩니다.

그럼 GCN은 데이터를 어떤 방식으로 표현할까요?

바로 Graph(그래프)입니다!

GCN : Graph

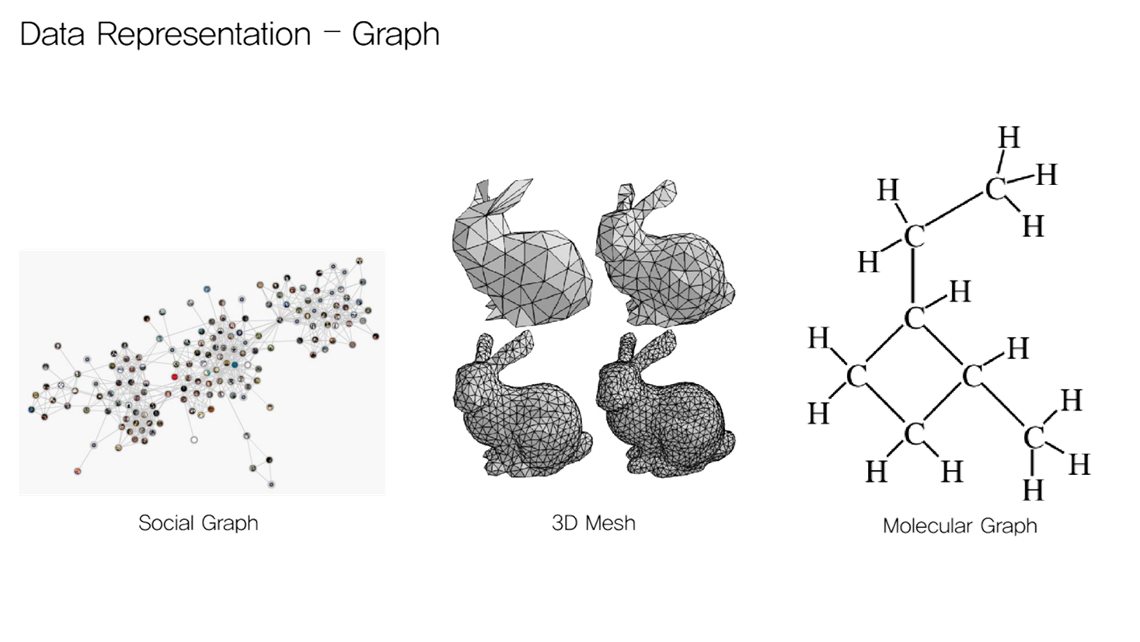
GCN에서 데이터를 표현하는 표현방식은 GCN에서의 G인 그래프로 표현합니다.

그래프의 정의는 일부 객체들의 쌍들이 서로 연관된 객체의 집합을 이루는 구조인데요.
그래프 데이터의 경우 앞에서 보았던 이미지 데이터처럼 시각적으로 나오거나, 시퀀셜 데이터처럼 연속적인 순서가 존재하는 것이 아닌 데이터가 많습니다.

그래프의 예로 소셜 네트워크상에서의 관계를 나타내는 소셜 그래프, 게임이나 디자인에서 사용되는 3D 메쉬, 화학분야에서 사용되는 분자 그래프 등이 있습니다.

이들의 특성은 서로 간 연관된 그래프로 표현할 수 있다는 점입니다.

GCN

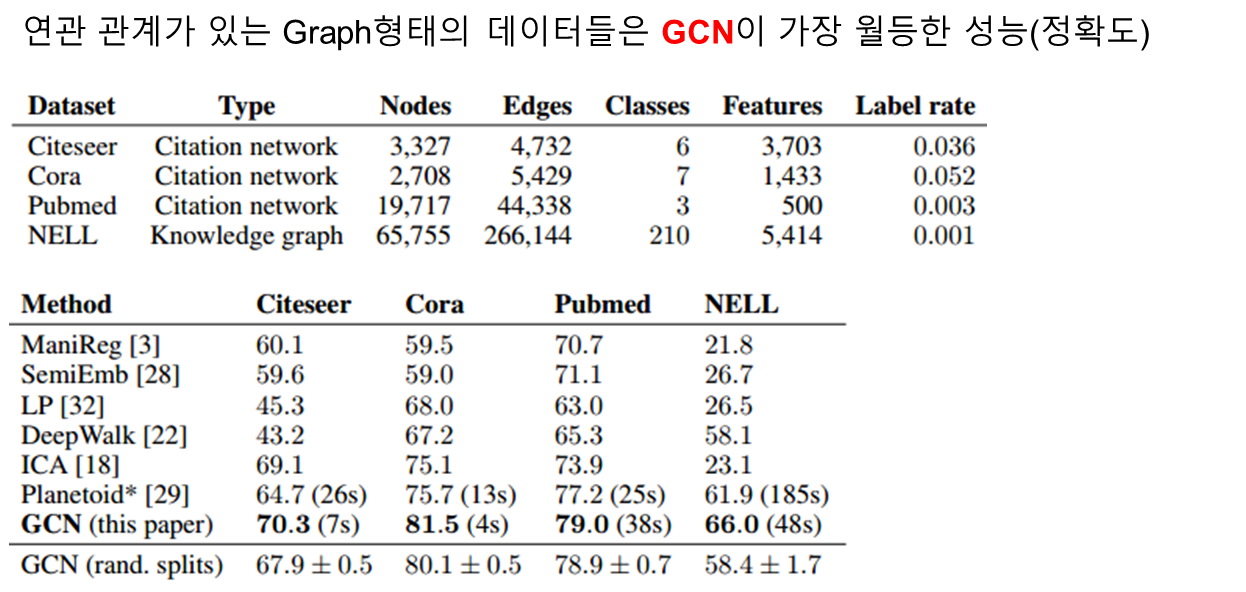
바로 이러한 연관된 그래프를 가장 잘 표현할 수 있는 방법. 즉, 데이터 셋을 표현하고 잘 분류할 수 있는 방법이 바로 GCN입니다.

Graph Structure

그렇다면 그래프의 구조는 어떻게 생겼을까요?

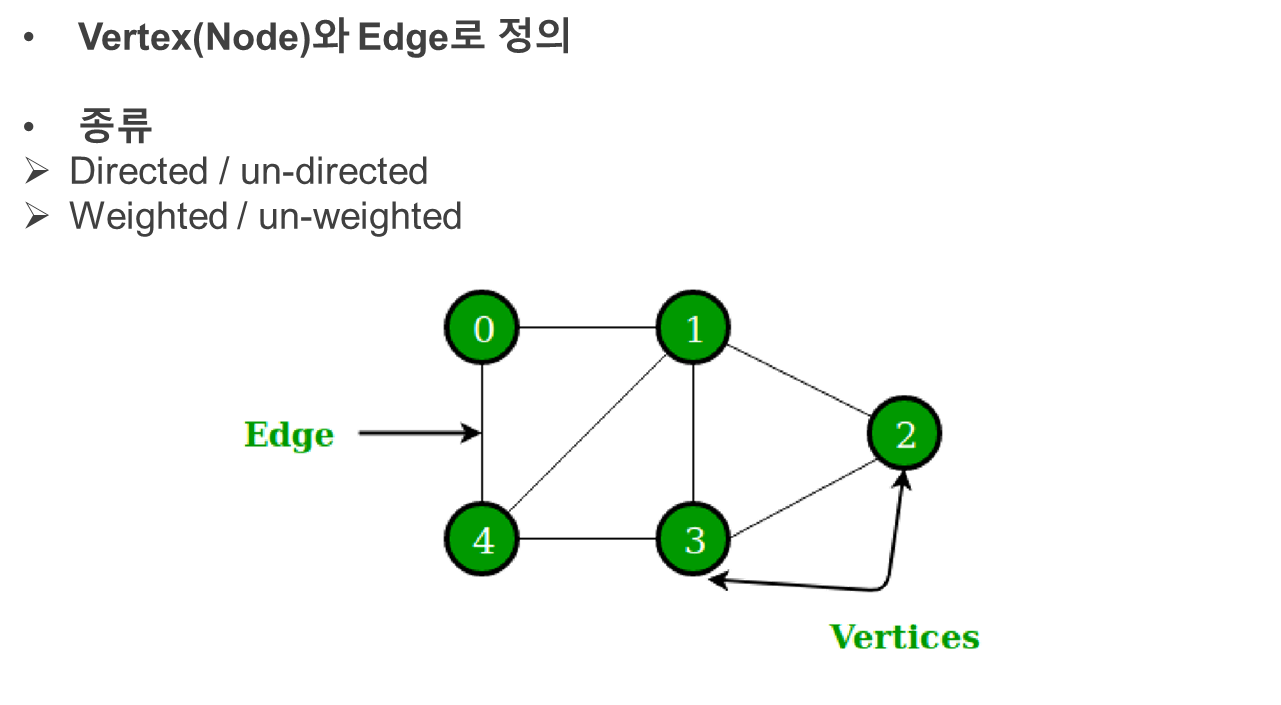
그래프는 Vertex즉, 노드인 꼭지점과 edge인 이러한 노드를 잇는 변으로 구성됩니다.
종류로는 방향성에 따라 구분되는 Directed / un-directed와
각각의 엣지들이 가지는 가중치의 유무에 따라 Weighted / un-weighted 로 구분됩니다.

adjacency matrix, node feature matrix

그렇다면 이제 이러한 그래프로 이루어진 정보를 어떻게 컴퓨터로 전달하여 사용할 수 있을까요?

행렬의 형태로 그래프를 표현하여, 컴퓨터에서 사용하게 됩니다.

주로 두 가지 matrix를 사용하게 되는데, adjacency matrix와 node feature matrix가 있습니다.

adjacency matrix의 경우, 노드간의 연결성을 나타내는 즉, edge에 관한 정보를 나타내고
node feature matrix같은 경우, 각각의 노드에 담겨있는 정보를 나타냅니다.

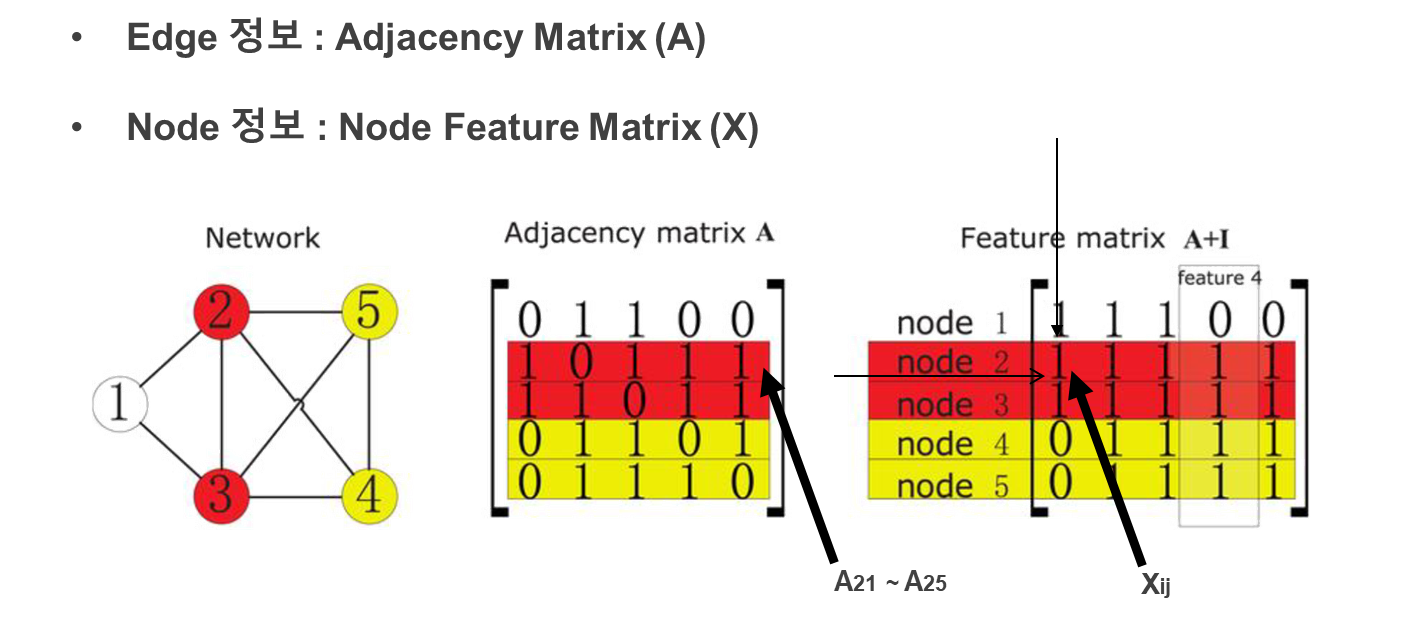
adjacency matrix란?

adjacency matrix부터 살펴봅시다.

n개의 노드가 있다면 adjacency matrix의 크기는 nxn이 됩니다.
여기서는 5개의 노드가 있으므로 5x5 크기가 되겠죠.

이러한 행렬 $A$에서 $i$번째 행, $j$번째 열에 있는 값 $A_{ij}$가 나타내는 숫자(0, 1)는 노드간 서로의 연결성을 나타냅니다. 이 때, 연결이 있으면 1로 연결이 없으면 0으로 나타냅니다.

예시

예를 들어 화살표가 가르키는 두번째 행을 보겠습니다.
두번째 행 $A_{21}$ ~ $A_{25}$는 2번 노드와 다른 노드들 간의 연결성을 나타냅니다.

자기 자신(2)을 제외하고는 다른 노드(1, 3, 4, 5)전부와 연결이 되어 있으므로 1로 표시됨을 알 수있습니다.

연결이 있으면 1, 연결이 없으면 0인 binary(이진)값을 가지며 이는 다른 노드들 또한 동일함을 알 수 있습니다.

※ 추가적으로 노드간 연결된 edge의 가중치를 나타낼 때는, 단순히 0과 1의 binary값 뿐만아닌 더 다양한 값을 사용할 수도 있습니다. (여기서는 넘어가도록 합시다.)

node feature matrix란?

두 번째로 node feature matrix의 경우 노드 개수 n만큼의 행을 가집니다.

여기서는 5개의 노드 이므로 5개의 행을 가지고, 사용자가 정의한 특성의 개수 $f$에 따라서 열의 개수가 결정됩니다.

예시

영상 이미지를 예로 들어보겠습니다. 각 노드가 픽셀을 나타낼 때, 해당 픽셀의 r/g/b값, 투명도, 밝기 이런 식으로 총 5개의 Feature가 픽셀에 있다 라고 가정합시다.

그렇다면 node feature matrix의 크기는 $n*f$ 이므로 5x5행렬이 되게 됩니다.

즉, 그림에서의 화살표가 나타내는 node feature matrix의 $X_{ij}$의 의미는 $i$번째 노드의 $j$라는 특성의 값이 얼마인지를 나타냅니다.

그림에서 보듯 2, 3(빨강)번 노드와 4, 5번(노랑) 노드는 특성이 일치(같은 색)하므로 node feature matrix에서 같은 값을 가지고 있는 것을 알 수 있습니다.

그림상에서는 0과 1로 표현되어있으나 r/g/b값이라면 0~255까지의 값을 가지듯, 더 큰 값으로도 자유롭게 표현할 수 있습니다.

Next

이렇게 GCN에서 G까지를 알아보았습니다!
다음 글에서는 GCN에서 C인 Convolution에 대해서 서술하도록 하겠습니다.