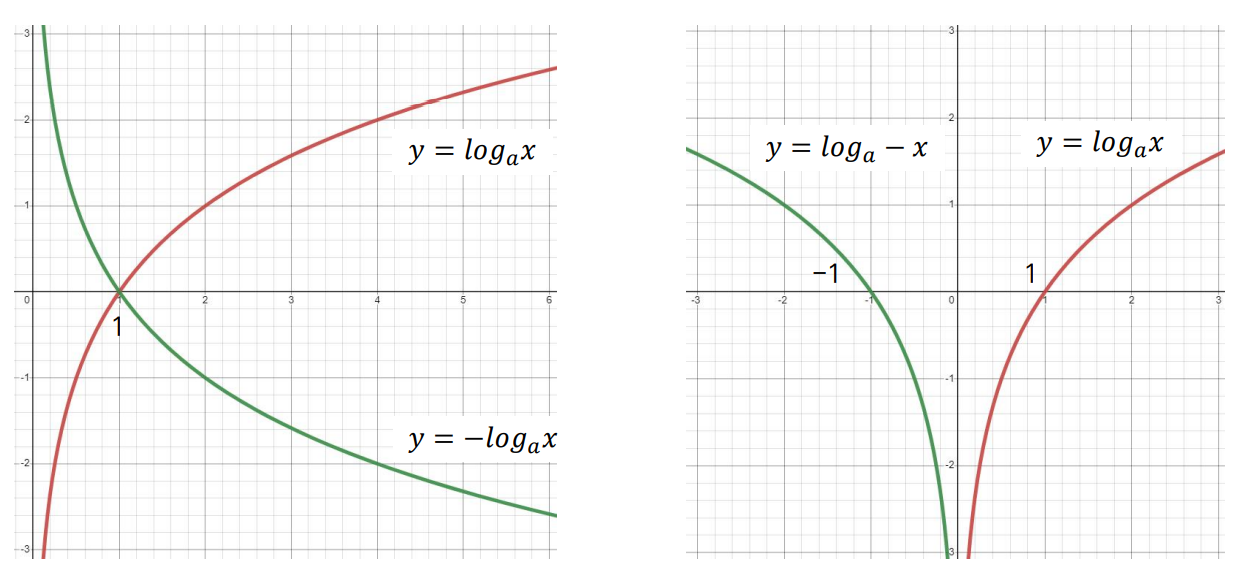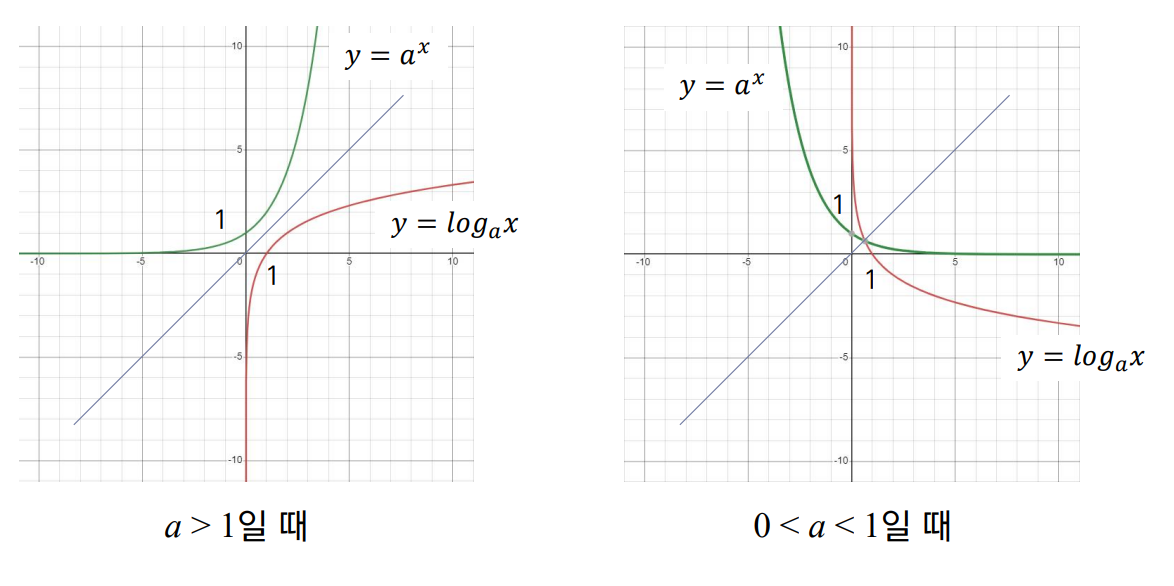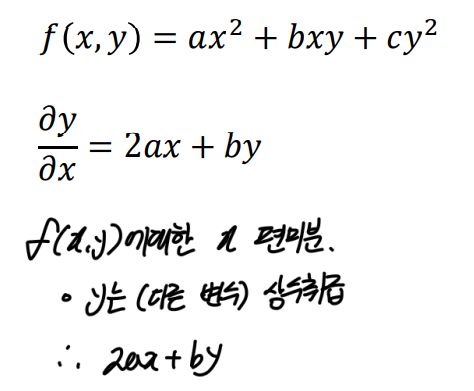딥러닝 기초 - part04. 딥러닝에 필요한 기초적인 수학 지식

🧩 Introduction

딥러닝이 무엇이고 어디에 활용하는가, 그리고 딥러닝과 머신러닝의 차이점까지 알아보았다.

이제 본격적으로 딥러닝을 하기위해 기초적인 수학 지식에 대해서 집고 넘어가도록하자.

📐일차함수 & 이차함수

함수란?
X값 하나에 대응되는 Y값 하나가 있는 이러한 이항관계를 함수라고 표현하고 쉽게, $f(x)=y$로 표현할 수 있다.

일차함수

• 일차함수는 $y = ax+b (a \neq 0)$로 표기할 수 있다.

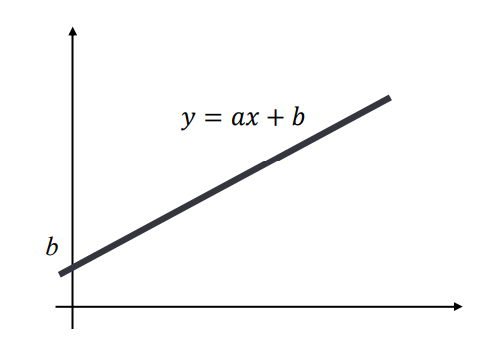
이차함수

• 이차함수는 $y=ax^2+bx+c (a \neq 0)$로 표기할 수 있다

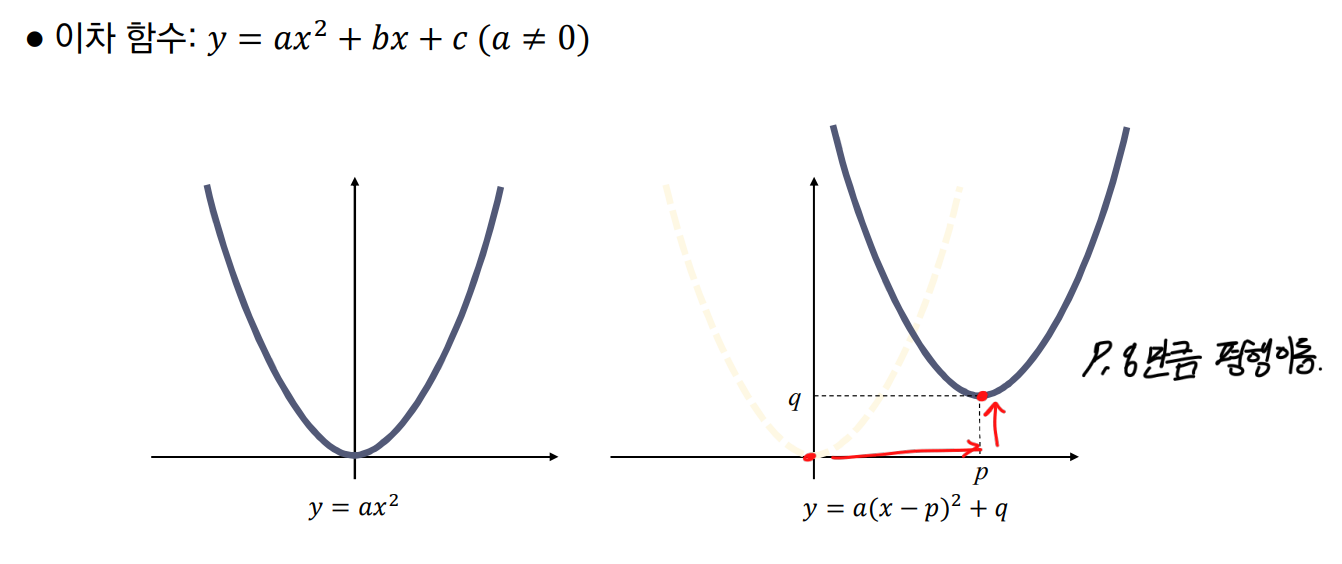
📐 지수 & 지수 함수

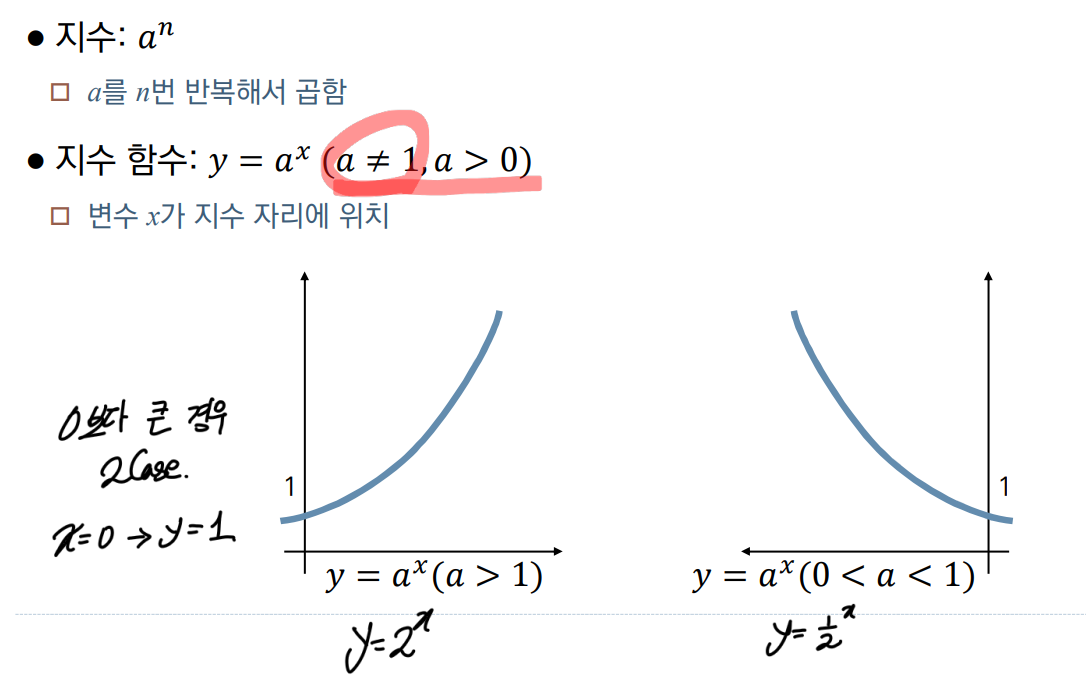
지수함수란 지수($a^n$)을 함수식으로 표현한 것이다.
함수식은 $y = a^x$가 되며, 이때 $a \neq 0$이다.
밑($a$)의 값에 따라 $a$가 0<$a$<1 사이에 위치할 때, $a$가 a>1 때 두가지로 분류할 수 있다.

• $a$가 0<$a$<1 경우 x에 대한 y값이 위로 발산하는 그래프 형태를 보이고
• $a$가 a>1 때 x에 대한 y값이 0에 수렴하는 그래프의 형태를 보인다.
  

📐 시그모이드 함수

이후, rogistic regression 파트에서 왜 이 함수를 사용하는지 알 수 있다.
일단은 이렇다~라는 것을 알고만 가자.

• $f(x)=$ $1\over1+e^{-x}$
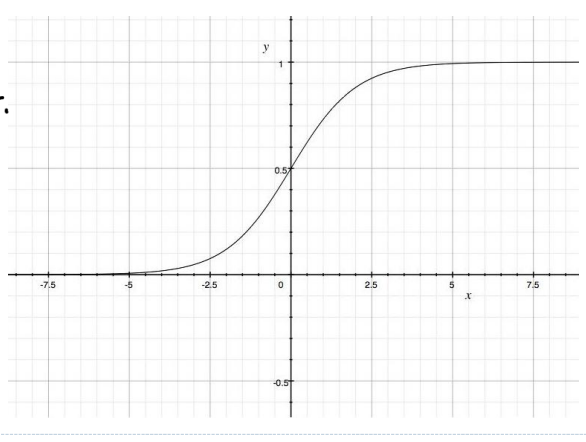
  밑이 자연상수 $e$(2.718281828..)를 가지는 함수를 말한다.
  수식적기 너무 힘들었다..
• x의 값에 무관하게 항상 출력값(y)는 0~1사이의 값을 가진다는 특징이 있다.

📐 로그 & 로그함수

기본 개념

지수 ↔ 로그간에는 서로 변환이 가능하다는 것을 고등학교 수학시간에 배운 적이 있을 것이다.
안 배웠더라도 상관없다. 지금 알아가자.

왼쪽 지수로 이루어진 식을 오른쪽 로그를 포함한 식으로 변경할 수 있다. (결국 똑같은 값이기 때문)
지수(c)부분이 그대로 좌항의 값으로 내려가고 나머지 밑과 우항의 값이 log의 밑과 진수로 내려간다.

다 알것이라 생각하나 혹시 모르니 몇까지 예제를 남긴다. 보면 이해가 갈 것이다.

• 

(그렇다. 같은 값이다 결국.)

• 로그함수는 다음과 같이 표현된다.
  $y=\log_{a}x$
  

🖇평행이동 / 대칭이동 예제

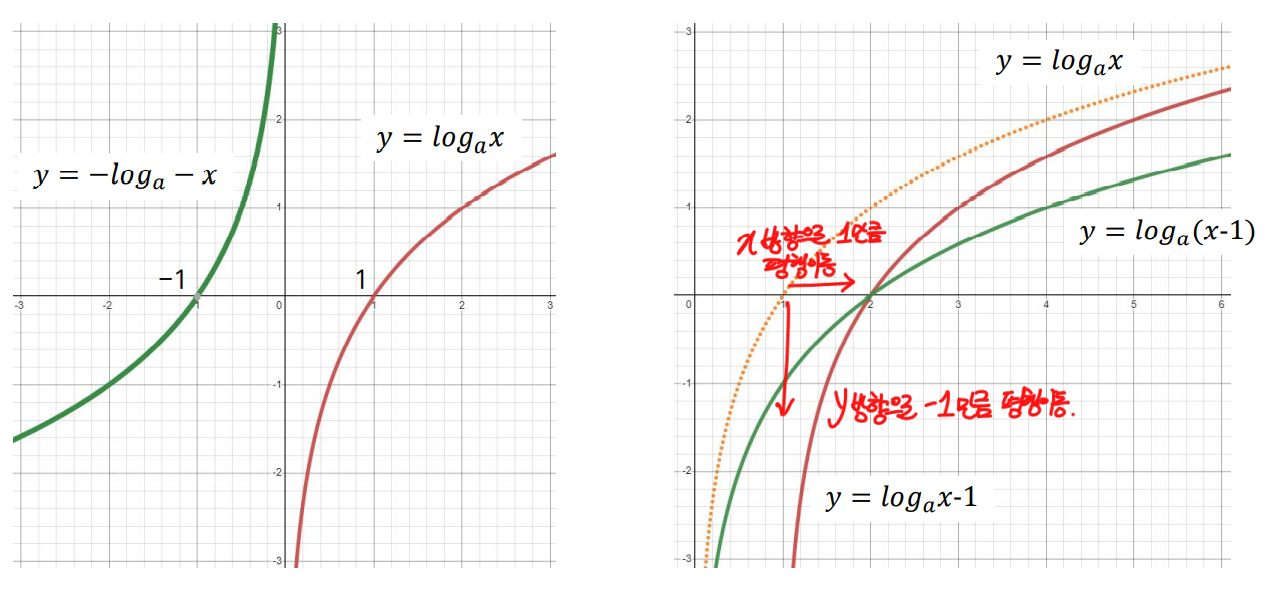
• 평행이동은 x, y값에 대해서 평행이동 된 값을 더해주면되고, 대칭이동의 경우 대칭이동할 축의 반대방향의 축에 -를 곱해준다고 생각하면 된다.

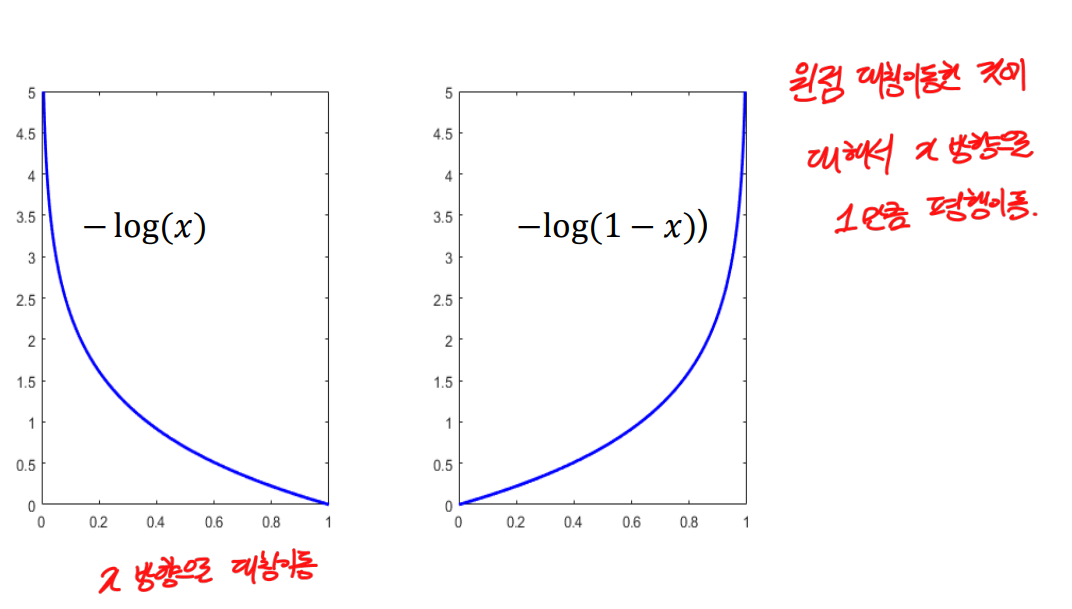
• log함수의 대칭이동

• 원점에 대해 대칭이동 / x방향으로 1만큼 평행이동(붉은색), y방향으로 -1만큼 평행이동(초록색)
  아무래도 평행이동 그림에 수식이 반대로 써진 게 아닌가 싶다.
  

• x축을 기준으로 대칭이동 / 원점에 대해서 대칭이동 후, x축으로 1만큼 평행이동
  
• 오른쪽과 같은 경우, $y=-\log_{10}{-(x-1)}$와 같이 식을 변환해서 생각하면 쉽다.

📏로그함수와 지수함수의 대칭성

위에서 살짝 나왔듯, 로그함수는 지수함수와 역함수 관계를 가진다. 따라서 대칭의 관계가 성립한다.

• 4가지 케이스 (지수2개, log 2개)에 대한 그래프는 다음과 같다,
  이러한 개형정도는 기본적으로 알아두는 것이 편하다.
• 대칭성이 성립하는 것을 확인할 수 있다.
  

📐 미분과 편미분

딥러닝에서 미분은 정말 중요하다. 왜인지는 이후 Gradient desent(경사하강법)을 통해서 설명한다.

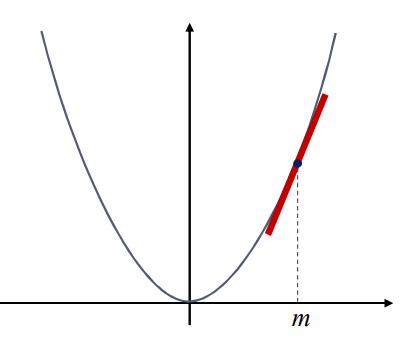
• 미분의 정의
  그래프에서의 순간변화율(기울기 값)을 구하는 과정"

• 미분 계수 ($m$에서의 기울기)
  • 어느 순간에 어떤 변화가 일어나고 있는지를 숫자로 나타낸 것
  • 그래프 한 지점에서의 기울기를 의미
    

〽평균변화율과 순간변화율

사실 딥러닝에서 평균 변화율을 사용하는 경우는 아직 보지 못했다. 미분에 대해서 정의하다보니, 이까지 나온것으로 생각된다.

💹 편미분

이 또한 이후에 배우겠지만, 짧게 말해 weight와 bias각각에 대해서 파라미터 값을 update해주어야 하므로 이러한 각각 미분을 하는 편미분이 이용된다.

• 함수에 여러 가지 변수가 있을 때 특정 한 가지 변수에 대해서만 미분
• 편미분의 수식 $\partial y \over\partial x$

'$\partial$' 해당 수식에 들어가는 저 문자를 사용하기 위해서 참 고생했다..
그냥 복사 붙여넣기로 넣어진 문자가 아닌, MarkDown문법으로 정의된 수식이다.

• 편미분의 예제
  
• 미분되는 변수$x$가 아닌 다른 변수들은 모조리 상수 취급된다.
  상수 취급 된다? → 미분시 0

이것으로 딥러닝에 대한 기초 수학적 지식을 알아보았다.
별 거 없다 (아직까진..)

이후는 수식을 작성하며, 사용했던 참고한 자료들을 나열하며 마친다.

✨ Velog 작성에 유용한 TIP

• ✨TIP
  위와같은 Velog에서 사용되는마크다운 문법의 경우 다음을 참고하자
  • 위키백과
  • 수식 입력 및 외부 링크 사용 - velog 공식
  • HTML과 같은 Velog 문법 사용