내가 낸 문제 내가 풀어보기 / 33711 - 내 이름 나무(G1)

서론

작년에 왔던 출제자! 사라지지 않고 다시 돌아왔습니다!

이제 핌 대회도 무려 4회를 맞이하였습니다. 이제 문제 출제도 좀 익숙해지는 것 같기도하네요.

이번에는 그래프 탐색 문제를 출제하였는데, 조금 신기하다 생각합니다. 한번 풀어보죠!

내 이름 나무 G1

문제 요약

• 임의의 노드에 이름이 붙어있다.
• 이름은 중복 될 수 있다.
• 이 이름은 가짓수는 최대 1,000가지이다.
• 같은 이름을 가지는 노드 쌍 사이의 최소 거리가 K 이하인지 구하여라

접근

일단 K 이하인지는 마지막에 판단하면 되기에 이 문제는 같은 이름을 가지는 노드 쌍 사이의 최소값을 구하는 문제입니다.

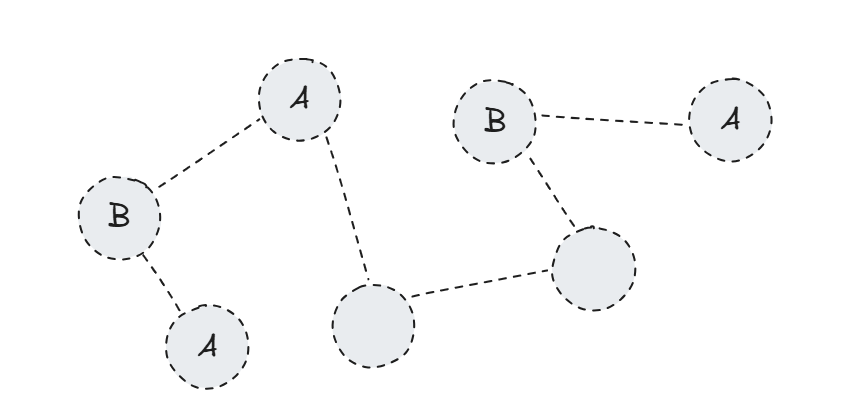
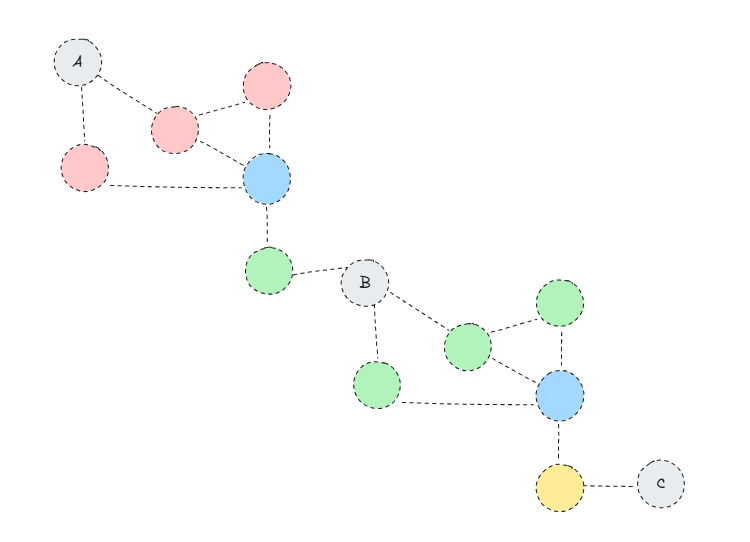
가령 위와 같은 그래프에서는

• A라는 이름을 공유하는 노드쌍(노드가 3개가 존재하기에 노드쌍 조합은 3가지 존재, 그리고 그 거리는 2, 4, 6)
• B라는 이름을 공유하는 노드쌍(노드가 2개 존재하기에 조합은 1가지 존재, 그리고 그 거리는 5)

이렇게 두 개가 존재하고 최소거리는 A에서 가장 최소거리인 2이게 됩니다.

일단 이것을 구하는 가장 간단한 방법은 그냥 모든 이름이 붙은 노드에서 BFS 탐색을 돌려보면 됩니다.

BFS에서는 진행과정에서 각 노드에 거리가 저장되기에 시작점과 이름이 같은 노드에 도착하였을때 그 거리를 저장하면, 해당 시작점에서 가장 가까운 같은 이름 노드까지 의 거리를 구할 수 있게 됩니다.

이것을 모든 이름 붙은 노드에 대해 돌리게 되면 답을 쉽게 구할 수 있습니다.

하지만 본 문제서는 N이 최대 35,000이기에 최악의 경우 모든 노드에서 모든 노드를 탐색하여 O(N^2)이 나오게 됩니다. 이는 주어진 시간제한에서 돌아갈 수 없습니다.

최적화

그럼 저희는 시간복잡도를 줄여야합니다.

가만히 고민해보면 같은 이름끼리는 반드시 중복된 탐색이 발생한다는 것을 알 수 있습니다.

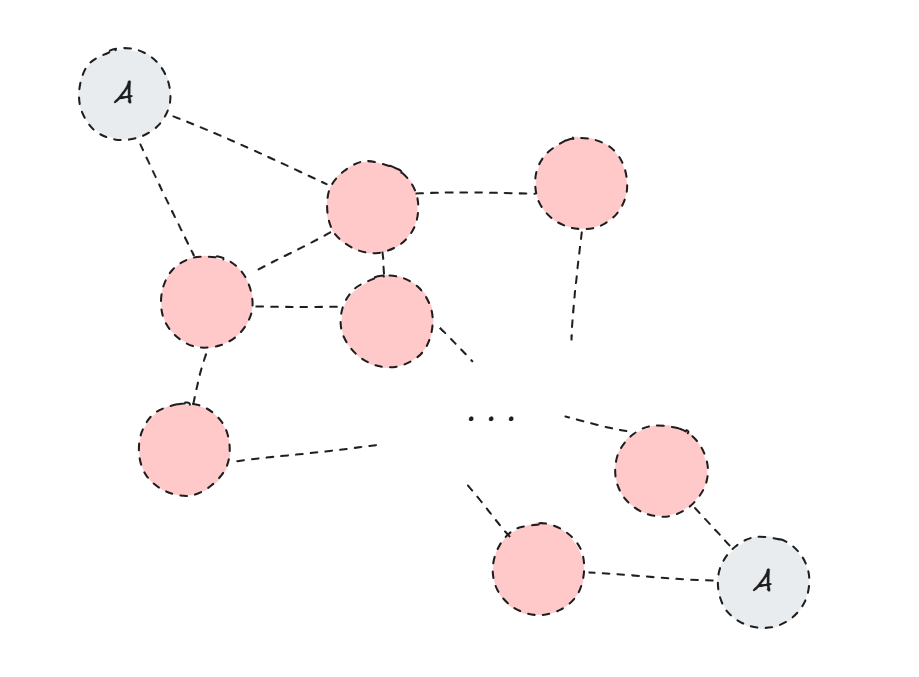
A라는 이름을 찾기 위해 A 이름이 붙은 노드를 모두 돌게되면 빨강색에 해당하는 부분에서 중복탐색이 발생하게 됩니다.

저 중복 탐색은 의미가 없는 탐색입니다.

만약 위쪽 A에서 빨간색 부분을 탐색하여 같은 이름(A)를 찾지 못했다면, 해당 노드들은 다른 아래쪽 A에서 탐색하여도 A를 찾을 수 없기에 답에 영향을 주지 못함.

즉, 저희는 이 중복 탐색을 줄이면 됩니다. 임의의 한 이름에 대해 그래프를 한번만 돌아 같은이름 사이의 거리를 찾을 수 있다면 시간복잡도를 O(이름 가짓수 * N) 으로 줄일 수 있게 됩니다.

어떻게?

그렇다면 어떻게 임의의 이름에 한번의 탐색으로 모든 쌍 사이의 거리를 구할 수 있을까요?

사실 저희는 모든 쌍 사이의 거리를 구할 필요가 없습니다. 최소값을 가지는 쌍만 찾으면 되는거죠.

---

먼저 BFS의 특징을 봐보겠습니다.

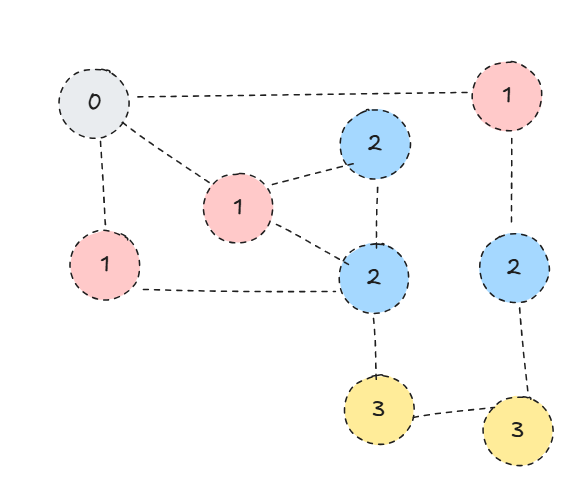
BFS의 탐색은 점점 뻗어나가는 특성이 있습니다.
시작점으로부터 거리가 N인 노드는 반드시 거리가 N+1인 노드보다 빨리 탐색이 됩니다.

우리는 BFS 과정에서 임의의 노드에 도달하면, 그 거리가 시작점으로 부터 가장 최소거리라는 것을 보장할 수 있습니다.

그렇다면 시작점 A와 B에서 동시에 BFS를 돌렸을때 임의의 노드 S에서 만나는 것을 가정해봅시다.

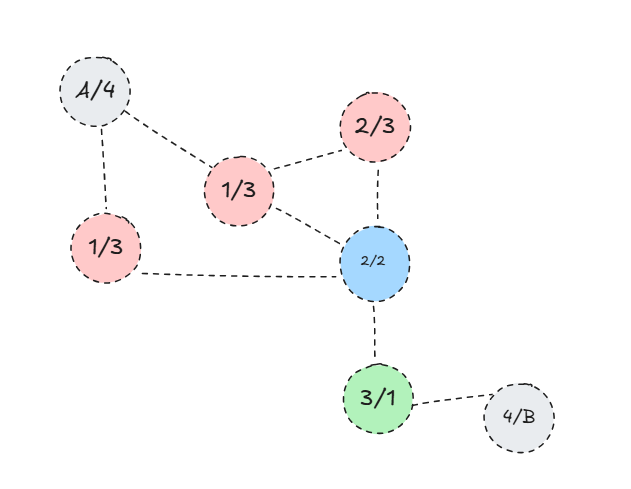
/를 기준으로 왼쪽은 A로부터의 거리, 오른쪽은 B로부터의 거리입니다.

BFS를 통해 임의의 노드에 도달하면 그 거리가 시작점으로 부터 최소거리라 하였습니다.

A에서 더 빨리 도달하는 노드는 빨간색, B에서 더 빨리 도달하는 노드는 초록색을 칠하였습니다.

그리고 파란색에는 둘이 동시에 도착하게 됩니다.

둘이 같은 노드에 도달하였을 때 두 시작점으로부터의 거리를 더하면 A와 B사이의 거리를 구할 수 있게 됩니다.

해당 그림에서는 4가 되겠네요.

하지만 여기서는 그냥 A에서 탐색해도 B에 도착하면 거리가 4라는 것을 알 수 있습니다. 왜 나눠서 탐색을 해야하죠?

그럼 시작점을 늘려서 A,B,C라 가정하겠습니다.

AB, BC, CA의 거리를 구해야합니다. 이 경우는 A에서만 탐색을 해서는 BC의 거리를 구할 수 없습니다.

그럼 B에서 탐색을 하게되는데 이 경우 A가 탐색한 곳을 경우에 따라(위의 N^2과 같이) 중복하여 지나가게 됩니다.

하지만 A,B,C에서 동시에 탐색을 하게 된다면 시작점이 다른 노드에 의해 이미 방문된 지점 도달하였을때 그 노드에 기록된 비용 + 현재 비용을 더하면 중복탐색을 하지 않고 비용을 구할 수 있습니다.

만약 A와 C같이 멀리있는, 즉 모든쌍의 거리를 구해야했다면 결국 A,B,C에서 탐색을 할 수 밖에 없지만, 가까운 두 쌍 사이의 최소거리를 구하면 되기에 이미 방문된 노드(파랑색)를 마주하면 멈출 수 있게 됩니다.

그럼 이것을 우리 문제에 적용해봅시다.

적용

임의의 이름에 대해 이름이 같은 모든 노드에서 동시 BFS를 시작합니다.

여기선 A로 해보겠습니다.

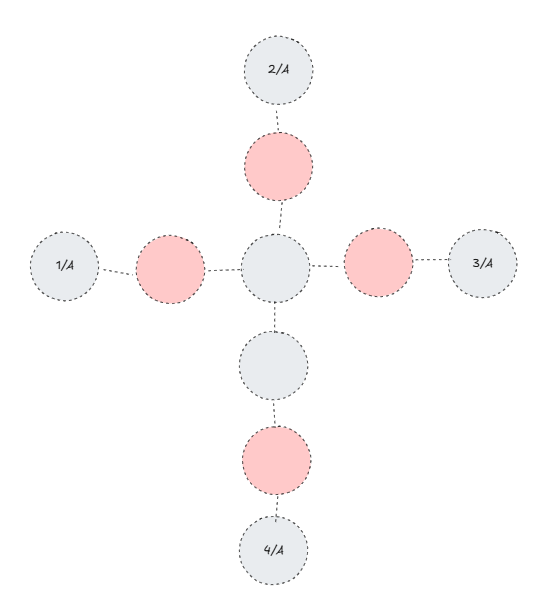
계속 진행해보죠

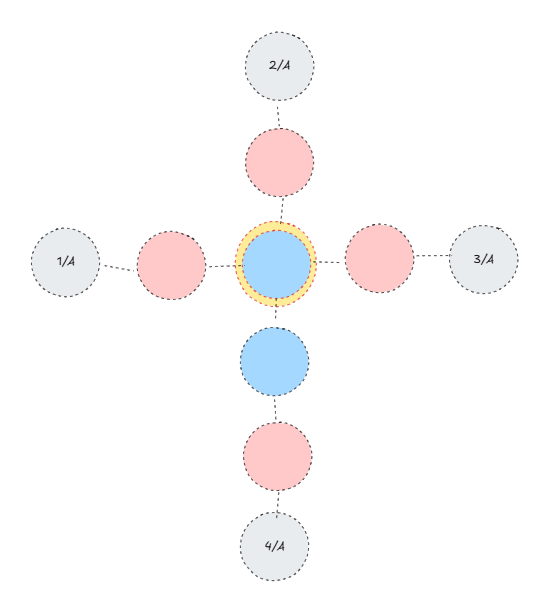
자 노랑 부분에서 시작점이 다른(1,2,3)노드 끼리 만나게 되었습니다. 우리가 앞서 이야기한 내용에 따라 비용을 구합니다. 4는 아직 탐색중이고 이후 반복에 역시 시작점이 다른 노드를 만나게 되지만, 최소거리가 아니기에 의미가 없습니다.

만약 앞서 이야기했듯 1-> 4와 같은 모든 거리가 필요했다면 N^2이 되겠지만, 최소거리만 필요하기에 저기서 탐색을 중단할 수 있게 됩니다.

요약하면 아래와 같습니다.

1. 모든 등장한 이름에 대해 같은 이름을 가진 노드를 모두 큐에 집어넣고 동시에 BFS를 돌린다.
2. 아직 방문되지 않은 노드라면 거리와 어느 시작점에서 방문한건지 기록한다.
3. 이미 방문되었고 시작점이 다른 노드를 만나면 최소거리를 계산하고 해당 노드는 큐에 집어넣지 않는다.

이제 모든 과정을 마친후 구해진 답이 K이하인지 구하면 됩니다.

마무리

태그는 멀티소스 BFS가 되겠네요.
시간복잡도는 O(이름 가짓수*N)이기에 O(1000*N)이 되겠습니다.

다들 보면 발상은 어렵지 않지만 증명이 까다로운 문제라고 많이 이야기하는 것 같습니다.